The image speaks for itself. Sorry about the language, but this is the most concise and precise way to say this.
Update 4-26-2020:
After Mr. Trump's exposition of the notion of injecting or ingesting known-fatally-toxic disinfectants to "cure" Covid-19 disease, the phone numbers for poison control around the country have fielded a lot of calls about this topic! And, the makers of those disinfectants have felt compelled to issue warnings NOT to ingest or inject these materials!
Science very clearly says DO NOT DO what Mr. Trump suggested! In matters of science, he is quite clearly far dumber, than the average fence post.
Mr. Trump now claims he was being "sarcastic" when he suggested that, but the video footage of him suggesting this to Dr. Birx very simply denies that claim. Period! End of issue! It is quite clear he will not admit to making a very serious mistake. Especially one that would be fatal to those who might follow it.
Add to that the recent absence of Dr. Fauci from the White House briefings. (Update 5-2-2020: the White House has blocked Fauci from testifying before Congress!) Fauci has contradicted Trump's ignorant lies on multiple occasions, accompanied by shouts of "fire Fauci" from Trump's most ardent supporters. Is anyone in their right mind now surprised by that absence?
OK, I understand that Mr. Trump's most ardent supporters are also deniers of science in multiple arenas. That much is quite clear from their positions on climate science and on the dangers of pollution, versus what humans might really be able to do. Perhaps that disparity is to the advantage of the country as a whole.
Applying the epithet "Branch Covidians" to his most ardent supporters, then perhaps letting them kill themselves, by injecting or ingesting bleach and isopropyly alcohol, or by defying quarantine, is actually appropriate. That way, there are fewer of them left, come November, to vote for him. Death cults do, in fact, lead to death. And Mr. Trump's most ardent supporters do indeed qualify as a death cult.
If you want to know why I say that (meaning the danger of glorious-leader death cults), then peruse the article "Beware of Leader Cults", posted 2-13-2020, on this same site.
Friday, April 24, 2020
Saturday, April 4, 2020
On the Covid-19 Pandemic
Update 7-14-2020: Well, we opened up too quickly, with too many people behaving like there is no disease problem. There is no reason why businesses and other things cannot be open, as long as careful attention is paid to stopping disease transmission. But too many people are either too stupid to understand the science, or too incapable of critical thinking not to be deceived by internet lies and conspiracy theories. The worst of which keep coming from our president and his ardent supporters, instead of actual leadership in a crisis. November is coming -----
Update 4-10-2020: see modeling analysis appended to the end of this article.
Update 4-11-2020: see also recommendations for how and when to end the quarantines appended below.
Update 4-23-2020: added second model; see update appended at end below.
Final Update 5-2-2020: evaluation of second model appended below.
****************************
Update 4-11-2020: a version of this basic article appeared as a board-of-contributors article in the Waco "Tribune-Herald" today.
The current pandemic is a disease about which we know little, for which we have no vaccine, and for which we have no real treatments. After this is over, we will know more, but for now, the only thing we can do is to use the same thing we have used for centuries: quarantining at one level or another, to slow its spread. Calling it "social distancing" makes no difference, it is still a simple quarantine.
Figure 1 -- Data on Particles Versus Filter Pore Sizes
Update 4-10-2020: see modeling analysis appended to the end of this article.
Update 4-11-2020: see also recommendations for how and when to end the quarantines appended below.
Update 4-23-2020: added second model; see update appended at end below.
Final Update 5-2-2020: evaluation of second model appended below.
****************************
Update 4-11-2020: a version of this basic article appeared as a board-of-contributors article in the Waco "Tribune-Herald" today.
The current pandemic is a disease about which we know little, for which we have no vaccine, and for which we have no real treatments. After this is over, we will know more, but for now, the only thing we can do is to use the same thing we have used for centuries: quarantining at one level or another, to slow its spread. Calling it "social distancing" makes no difference, it is still a simple quarantine.
Here is what we do know, as of this writing, learned the hard way as the epidemic sickens
and kills people. It seems similar
to, but not the same as, the 1918 "Spanish Flu"
pandemic. We have not seen this
dangerous a disease since then. It is a
once-in-a-century event.
Covid-19 seems to be at least as contagious as, and perhaps more contagious than, the 1918 flu.
It seems to have a similar death rate (the number who die compared to
the number thought to be infected),
which is somewhere around 10 to 20 times higher than ordinary influenzas. Those are seriously-dangerous characteristics.
There seems to be another unusual characteristic that
combines with the other two to make Covid-19 a truly dangerous threat. It seems to be more generally spread by
people showing no symptoms, than by
people who are just getting sick and beginning to run a fever.
That makes all of us potential "Typhoid Mary"
carriers of the disease. It also makes
taking temperature rather useless as a screening tool to determine who might be
infected, and who might not be. Without
massively-available testing, one must
presume that all other persons are contagious,
which argues for using stricter levels of quarantine.
So far, it is thought
that the Covid-19 virus is spread within the moisture droplets ejected by
sneezing or coughing, or even by
talking. 5 minutes talking spews the
same droplet numbers and size distribution as one cough. A sneeze just spews a lot more. The Covid-19 virus does not seem to be able
to remain airborne outside of those droplets, the way a chickenpox or measles virus does.
Masks vary in their effectiveness against particle
sizes. It is hard to breathe through a
mask that stops particles the size of a large bacterium. No mask stops a virus particle. But even a simple cloth bandana will stop
most of the moisture droplets from coughing or sneezing, as does about 6 feet of space (the droplets
quickly fall to the floor). See Figure 1 at end of article.
What that means is that the new CDC recommendation to wear
masks in public is not to prevent the infection of the mask wearer, but to stop the mask wearer from infecting
others. It would protect the wearer only
when someone got right in their face to sneeze,
cough, or talk at very close
range. The 6 foot distance rule already
stops that effect.
The recommendation to wear a mask is actually based on this
uncomfortable reality: that many
seemingly-well people are actually infected,
just not showing symptoms, and
are walking around spreading the disease.
This "Typhoid Mary" effect is not common, but may well be the case with this particular
virus.
As already indicated,
a simple bandana will work. Leave
the real surgical masks for the health professionals. They need them. We ordinary citizens do not. When you go to the store, wear a bandana or a home-made mask. That's all you need, to protect others. The 6 foot rule protects you.
And for Heaven's sake,
quit panic-buying toilet paper and other supplies! There is plenty being made, and plenty in the supply chain, for everybody's needs. The shelves are bare because so many folks
panicked and took far more than their share (their "share" being what
they really need). Shame on you!
Predictions about this pandemic are still guesswork. The CDC figures show a peak of 100,000 or
more deaths in about another month.
Maybe a month or two after that,
it will be more-or-less over, and
we can safely re-open our lives and businesses.
But that's a guess, and it will
likely change. See Figure 2 at end of article.
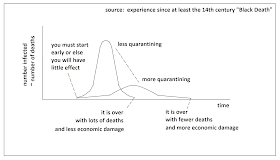
Had we started with the quarantining a month or two sooner
than we did, the death totals would have
been lower, but the time to the end of
this gets longer. Time spent shut down
costs all of us money and jobs.
That is the inevitable tradeoff: lives versus money. And it is quite the
serious effect, make no bones about
that. Job losses are already beginning
to resemble those of the Great Depression of the 1930's.
But almost all of your mothers and churches taught you to
value lives over money, that valuing
money over lives was evil! Think about
that, when you vote. Not just next time, but from now on.
Figure 2 -- How Quarantining Works, and What It Does
Update 4-5-2020:
The best numbers I have seen on Dr. Fauci’s curves and
predictions, as of end-of-March, say that with “social distancing”
quarantining in place, US deaths may
accumulate to 100,000 to 240,000 people lost.
That death rate trend should peak out somewhere in early May. Without the quarantining measures, something like 2 million deaths would be
expected. Maybe more.
Just to “calibrate” the threat of this thing, the US lost 407,300 soldiers in WW2, for a 1939 population of 131 million. That’s 0.31% of the population dead
from war.
With Covid-19 at a population of 325 million today, it is 0.03-0.07% of the population dead with
quarantining, and something like about
0.6% of the population dead without quarantining. You don’t credibly compare this pandemic to yearly
traffic deaths or the H1N1 epidemic. You
compare it to the casualties of a major world war.
Based on the numbers published in the newspaper, the US death rate appears to be near 2% of
known cases of infection. For Dr. Fauci’s
predicted death accumulation numbers,
that corresponds to something like 5 to 12 million accumulated known infections. That’s about 1.5-3.7% of the US population
infected, and 0.03-0.07% of the
population dying of it. These numbers
are clouded by uncertainty, because
without widespread testing, we cannot
know the real number of infections.
Using the rough-estimate 2 million deaths for no
quarantining, and the same 2% death rate
of those infected, the accumulated infections
would be about 100 million, which is 31%
of the US population. Quarantining is
thus very, very important, by about a factor of 10 on the total
infections, and on total deaths. So,
those who deny or ridicule the risk are dead wrong, if you will forgive my choice of words.
According to Wikipedia,
the 1918 Spanish flu killed something like 1-6% of the world
population. The same article gives these
statistics for the US: about 28% of
the population became infected, and
about 1.7% of those infected died of it.
The
death rate among those infected is quite comparable between Covid-19 and the 1918
flu. The number of expected Covid-19 infections
is lower, probably because of our quarantining
efforts, despite our delay getting
started. The estimate of infections
without quarantining is actually quite comparable to 1918.
The Covid-19
pandemic really is an event comparable to the 1918 flu pandemic. We have not seen such a thing in 102 years.
This is quite serious,
so I reiterate the recommendations I gave above:
#1. Stay away from crowds and gatherings, and when you must go out, stay at least 6 feet apart (which is what
protects you from infection, not any
mask you might wear).
#2. If you must go out where 6 feet apart is not feasible, wear a bandana or home-made mask to protect
others in case you are unknowingly contagious (save the real masks for the
health care folks who need them).
Corollary: if you are sick in any way, DO NOT GO OUT.
#3. Stop panic-buying and hoarding supplies, there is no need for that.
#4. Watch what your public leaders do (not what they say) to
judge whether they values lives over money, or not.
Then stop re-electing those with the wrong priorities.
********************
Figure I – Shape and Characteristics of the Unscaled Pulse
Function
Figure II – Shape and Characteristics of the Unscaled
Accumulation Function
Figure A – CDC Data for U.S. Accumulated Cases of Covid-19
Infections as of 8 April 2020
Figure B – Recreated CDC U.S. Daily Case Rate Data as of 8
April 2020
Figure C – Comparison of Raw U.S. Data Versus 3 Different
Moving Averages
Figure D – Comparison of Model and Data for U.S. Accumulated
Cases
********************
Update 4-10-2020:
Pulsed events like the daily infection rate for Covid-19 are
actually well-modeled by the mathematics of something called the “logistic
distribution”, which is similar to, but numerically a little different from, the “normal distribution” in statistics. The daily rate corresponds to a pulse
function f, and the accumulated total
follows a S-curve shape corresponding to the F-function. F is the integral of f (which means f is the
derivative of F). F is defined from 0 to
1, so you have to scale it to apply it
in the real world. The following
mathematics were obtained from Wikipedia under the article name “Logistic
Distribution”.
Derivative
(like a probability density):
f(x, µ, s) = exp(-(x - µ)/s) / s[1 + exp(-(x - µ)/s)]2
Cumulative
function (S-shaped accumulation curve):
F(x, µ, s) = 1/[1 + exp(-(x - µ)/s)]
Variable
definitions:
x is the
independent variable, usually time in
applications, a real number, from – infinity to infinity
µ
is the location variable, center of the
f-distribution, and location of half the
total accumulation
s is the
scale variable > 0, a measure of the
distribution width; a bigger s is a
flatter and longer pulse
F varies from 0 to 1;
you have to scale it by the total accumulated T
The shape of the pulse function is shown in Figure I for
multiple values of the 3 model parameters.
The smaller s is, the “peakier”
the pulse. The location parameter µ
merely moves the shape left or right on the graph. The larger T is, the taller the pulse, as a direct scale factor.
The shape of the unscaled S-curve accumulation function is shown in Figure II. The smaller s is, the steeper and shorter-in-time the S-curve
shape is. The location parameter µ
merely shifts the shape left or right,
same as with the pulse function.
The T factor merely scales the shape from its 0-to-1 variation to
whatever numbers your data are.
To model a pulse of something that eventually totals to T
instead of 1, scale up both the
cumulative and the derivative with the factor T. Thus:
Derivative
(pulse function)
Pulse rate vs time = T f(x, µ, s) = T exp(-(x - µ)/s)
/ s[1 + exp(-(x - µ)/s)]2
Cumulative
(S-curve function)
Accumulated total vs time = T F(x, µ, s) = T/[1 + exp(-(x - µ)/s)]
At the peak of the pulse in your real-world data, there is a max rate with time, and a location in time, and in the accumulation function at that same
location, the total is exactly half the
eventual total. The model parameters
can be calculated quite easily from those three pieces of data, if you can confirm you have actually seen
the max of the pulse. Here is how
you do that:
Where
in x it peaks is µ
T = 2 times
the accumulated total-at-peak
s =
T/(4 times the peak rate)
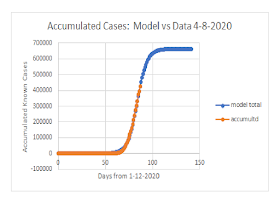
I went on the CDC website 4-9-2020 and retrieved their posted
Covid-19 Infections data as of 4-8-2020.
They had posted both accumulated cases,
which I used, and a daily case
rate vs time from a presumed infection date,
which did not share the same time scale.
I did not use the daily case data because of differing assumptions, and because they said in no uncertain terms
that the final week or so was clouded by as-yet unreported data. Here in Figure A is the CDC’s own accumulated case
data (as of 8 April 2020) vs time from 12 January 2020, as plotted from the spreadsheet in which I
put it.
The accumulated data are simply summed from one day to the
next, from the daily reported infections
data. So, I simply recreated their daily case rate data
by differencing the accumulated data from one day to the next. That way everything shares the same sources
and assumptions. See Figure B.
Early on, the numbers
are small, and even a large-percentage
inherent scatter is not significant. Later, as the numbers climb, a large-percentage inherent scatter becomes
very significant, actually to the point
of obscuring the trend. There would seem
to be a suggestion of the daily case rate bending over a peak value, but picking a number for the peak point would
be difficult indeed. This some sort of
averaging is needed to actually “see” the peak in the data well enough to
quantify it. I tried the moving-average
technique, with a 2-day average, a 5-day average, and a 3-day average, as seen in Figure C.
The 2-day moving average did not fully suppress the up-down
scatter variation, but showed very little
“lag” in its trend behind the raw data.
The 5-day average suppressed the scatter, but lags the data trend by about 4-5
days, which is too much. The 3-day average showed the peaking behavior
the clearest, and with about a 2-3 day
lag behind the actual data trend.
The daily case rate seems to peak at about 32,400 cases per
day at day 86 in the 3-day moving average data.
Its rise trend is seemingly 2 days too late in terms of the rise before
peaking. So revise the peak date
to day 84, keep the 32,400 cases, and read the accumulated case data at day 84
(not 86) for about 331,000 accumulated cases at the peak point. The corresponding T, s, and
µ
data for the model are T = 662,000 final total cases, a scale parameter s = 5.108 days, and a location parameter µ =
84 days (on the graph time scale).
That model matches the accumulated case data quite well, as shown in Figure D. If you do not compensate for the lag of the
moving average technique, and use the
wrong µ, your model fails to match the initial upturn (near
day 60 to 70).
The same choices of parameters do a good job matching the
daily case rate data, as long as you compare
it to the moving average that reveals the peak.
Like with the accumulated data,
if you do not compensate for the lag of the moving average, then the model fails to match the initial
upturn in the data (again near day 60-70). This is shown in Figure E.
Figure E – Comparison of Model and Data for U.S. Daily Case
Rates
This case study illustrates the inherent difficulty in
choosing the “right” model parameters T,
s, and µ
unless you have already reached the peaking daily case rate in your data. This is due to the mismatch around the
initial upturn if you do not compensate for your moving average lag. There are multiple combinations of the
parameters that might match up the tail of the daily case rate distribution
over time, but most of these will not
correctly predict the peak. And the
inherent scatter problem forces you to use a moving average to “see” the
peak, which inherently introduces the
lag that causes the error, if not
compensated.
All that being said,
with a peak you can “see” and quantify,
this modeling technique becomes very accurate and very powerful for
pulsed events like epidemics, as the
plots above indicate. As a nationwide average, the U.S. Covid-19 epidemic seems to have
peaked just about 5 April 2020 (day 84 in the plots), at about 32,400 cases per day reported, and an expectation of being “over” by about 11
May at ~100 cases/day at the earliest,
or at worst about June 1 with 2 cases /day in this model, and with about 661,000-to-662,000 total
accumulated cases.
You do NOT release the quarantine restrictions until
the event is actually effectively over!
Relaxing just after the peak pretty-much guarantees a second pulse of
infections just about as bad, and just
as long, as the first. To propose doing so is a clear case of
valuing money over lives, instead of
lives over money. Valuing lives over
money is what your mothers and your religious institutions taught to most of
you readers! I suggest that you use it
as a criterion to judge your public officials.
A final note:
this same pulse model has been used to predict resource extraction and
depletion. The most notable example was
geologist M. King Hubbert trying to predict “peak oil”. One of his two best models came very close to
predicting peak oil from data he had long before the peak actually
occurred, something very difficult at
best. Since then, the model has diverged from reality and thus fallen
into disrepute.
Since that peak, the
development of then-unanticipated cheap fracking technology has not only made
fracked oil and fracked gas available,
their simple availability has vastly increased the total recoverable
resources available. Those are
very large and very fundamental changes in the assumptions underlying the
formulation of any predictive model.
That’s analogous to the situation of a second wave of infections in the
epidemic application.
A new peak fracked oil/gas model would be the right thing to
do to respond to these developments. And
if recovery technology improves much past the current 2-3% recovery rates, yet a further new prediction would be
warranted. That’s just the nature of prediction
models being sensitive to the assumptions underlying them.
*****************
*****************
Update 4-11-2020:
These predictive models cannot tell you when to lift
the quarantine! Period! These exponential functions never, ever predict when the daily case rate goes to
zero. Mathematically, they cannot.
Instead, you have to watch (1) the daily infection
rate field data and (2) you have to
determine from experience during the epidemic, what the actual incubation time really is. You CANNOT lift the quarantine, until the daily infection rate has been zero
for an interval longer than the observed incubation time. There is NO WAY around that requirement! To do otherwise is to value money over
lives, an evil according to the morality
you were taught as a child.
If the observed incubation time is 7 days, then 8 or 9 or 10 days of zero infections
ought to do the trick. If the observed
incubation time is 10 days, then 11 or
12 or 13 days of zero infections ought to do it. If the observed incubation time is 14
days, then something like 15 or 16 or 17
days ought to do. There is simply no
way around such a criterion, if you
intend to be moral and value lives above money!
A caveat: this
needs to be on a regional basis, not
nationwide. That is because the
infection pulses did not all start at the same time around the country. They will not last the same interval, nor end,
at the same time. A
national edict to end the quarantine by this or that date is just wrong
technically, and demonstrably
immoral by the criterion I have offered. Regions can de-quarantine, but travel between them should stay
restricted until the last region is past the crisis.
*********************
Figure I – Increasingly Erroneous First Model
*********************
Update 4-23-2020:
As time went by, the
first model I set up looks ever poorer.
It was clearly not “right” in the sense that the predicted ultimate total
accumulated cases of infection were quite demonstrably wrong by 4-21-2020, using the published CDC data for the US. A lot of that can be attributed to the wild
scatter in daily rates about the peak point,
making it hard to quantify that peak point. This is shown in Figure I.
So, I repeated the
process as of 4-21-2020, obtaining a
second model. It has about the same peak
daily rate, just a bit lower and later
in time, with a larger accumulated case
number at that later time. This led to a
larger scale factor with a broader peak,
which matched the peak data quite well.
However, out in the
initial “tail” the match is not as good,
as can be seen in both the accumulated and daily rate data in Figure
II. And,
the time interval is longer. We
will see as time goes by whether this is really significantly better than the
first model. I think it is, but I’d also bet it will be “wrong”, too.
Figure II – Second Model at its Inception
This just emphasizes the point I tried to make in the
article: that these models are quite uncertain
even if you have peak data. If you
don’t, this is even more
uncertain. Exact predictions from
the model are not the point of doing this.
The trend shapes and behavior are the real goal.
This modeling process gives you only a crude idea what the
time interval will be from peak daily rate to no more new infections. That would be half the width of the
predicted pulse of daily rate data.
It’s only crude, but it’s far
better than nothing. My first model’s
pulse was about 70 days wide. The second
model’s pulse is about 130 days wide,
ending well into June.
It would appear from my experience here that predicting the
ultimate infection total (where the accumulated curve levels out) is even more
problematical than modeling peak behavior.
That seems significantly more uncertain than identifying the peak in the
daily rate curve.
Clearly,
ultimately, one must live through
the epidemic event, and just use the
actual data after it is all over, if one
wants accurate statistics. You won’t get
that from this modeling activity.
But, the other thing
I want to point out is that the peak curve shape in the daily rate data is
symmetrical. There is a fall-off
over time after the curve peaks,
it does NOT immediately crash to zero!
This is modeling a very real effect: after the peak, the daily infection rates are not zero for
some time interval, meaning there are
still infectious people walking around out there and spreading the disease! Ending the quarantine during this time
guarantees a resurgence, a second wave
that starts everything again from scratch.
You have to start your quarantine all over again! And the longer that goes on, the more jobs and money everyone loses. There is no way around that!
This
model behavior, which matches real-world
experiences, is exactly why I say you do
not end the quarantine until your daily infection rate has zeroed, and has been zero for longer than the microbe’s
incubation time. The
health professionals would agree with me,
not the politicians who want to end it too soon, just so that so very much money is not lost.
Once again, I
submit that you should use a simple criterion to judge whether public officials
have your best interests in mind: they
either value lives over money, or
they don’t. If they don’t, then you don’t want them making decisions for
you. Simple as that.
Where did I get that?
From the moral teachings just about all of us got from our mothers and
our churches. It’s a question of moral
fitness. That has to take precedence. And nearly every one of you readers knows
that, somewhere deep down.
Final Update 5-2-2020:
The CDC quit updating the national database that I was using
as my data source. They said modeling
communities was more appropriate than the entire nation. And I believe that may be correct, as the totals for states show mostly steady
or still-rising daily cases, strongly at
variance with each other. As a
result, I am no longer able to update
the 4-21-2020 model posted in the previous update. The last reliable data I have are for
4-27-2020.
However, as can be seen
in the figure, the daily infection rate
appears to be defying the previous interpretation of a peak in daily cases about
4-13-2020. There was a bit of a downward
trend, but in the last few days it has
trended sharply upward again. Possibly
this is related to some states ending quarantine measures, trying to reopen for business, especially without adequate testing and
contact tracing. Or it may just be the
inherent variability in the data. There
is no way to know.
From what I have read about the 1918 flu pandemic, here in the US there was the initial pulse of
infections, followed by two resurgence
peaks in daily rates, for a total of
three. I added that qualitatively to the
figure.
This Covid-19 disease epidemic seems similar in many ways to
that earlier epidemic. It is both highly
infectious (meaning easily transmitted),
and has a higher death rate than most other flus. The most dangerous aspect seems to be “asymptomatic
carriers”, meaning “Typhoid Marys” who
have the virus, are contagious, but do not know it because they are not sick. For most of you, the mask you are asked to wear in public is
to protect the public from you! You may
well have the virus and not know it.
Multiple pulses and “Typhoid Mary” transmission may be why
some authorities are now warning that the pandemic may be with us for as much
as 2 years yet. We are going to have to
figure out how to get back to business while at the same time interrupting the
transmission of this disease. It would
appear that we do not yet know how to do that successfully! All that we do know is that the pre-pandemic
status quo is NOT it! So for now, wear your mask and keep your distance, when in public.
Wednesday, April 1, 2020
Entry Heating Estimates
The following discussions define the various heating and
cooling notions for entry stagnation heating, in terms of very simple models that are known
to be well inside the ballpark. How to
achieve the energy conservation balance among them is also addressed. This is more of an “understand how it
works” article than it is a “how to actually go and do” article.
Convective Stagnation Heating
The stagnation point heating model is proportional to
density/nose radius to the 0.5 power,
and proportional to velocity to the 3.0 power. The equation used here is H. Julian Allen’s
simplest empirical model from the early 1950’s,
converted to metric units. It is:
qconv, W/sq.cm = 1.75 E-08 (rho/rn)^0.5
(1000*V)^3.0, where rho is kg/cu.m, rn is m, and V is km/s
The 1000 factor converts velocity to m/s. This is a very crude model, better correlations are available for various
shapes and situations. However, this is very simple and easy to use, and it has been "well inside the
ballpark" since about 1953. This is
where you start. See Figure 1.
Figure 1 – Old, Simple Model for Entry Stagnation Convection Heating
Plasma Radiation Stagnation Heating
There are all sorts of correlations for various shapes and
situations. However, to get started, you just need a ballpark number. That comes from the widely-published notions
that (1) radiational heating varies with the 6th power of velocity, and (2) radiation dominates over
convection heating at entry speeds above 10 km/s. What that means is you can use a very
simple radiational heating model, and
"calibrate" it with your convection model:
qrad,
W/sq.cm = C (1000*V)^6, where V
is input as km/s
The 1000 factor converts speed to m/s. The resulting units of the constant C are
W-s^6/sq.cm-m^6. You have to
"calibrate" this by evaluating C with your convective heating result
at 10 km/s, and a "typical"
entry altitude density value, for a
given nose radius for your shape:
find qconv per above at V = 10 km/s with
"typical" rho and rn,
then
C, W-s^6/sq.cm-m^6 = (qconv at 10 km/s)(10^-24)
This should get you into the ballpark with both convective
and radiation heating. Figure both and then
sum them for the total stagnation heating.
Below 10 km/s speeds, the
radiation term will be essentially zero.
Above 10 km/s it should very quickly overwhelm the convective heating
term.
As an example, I had
data for an Apollo capsule returning from low Earth orbit. I chose to evaluate the peak stagnation
heating point, which occurred about 56
km altitude, and about 6.637 km/s
velocity. See Figure 2.
Dividing that convective heating value of 55.72 W/sq.cm by the velocity
cubed, and then multiplying by 10 km/s
cubed, I was able to estimate stagnation
convective heating at 10 km/s and 56 km altitude as 190.59 W/sq.cm.
Dividing that value by 10 km/s to the 6th power
gave me a C value of 1.90588 x 10-4,
to use directly with velocities measured in km/s, for estimating radiation heating from the
plasma layer adjacent to the surface.
The resulting trends of convective,
radiation, and total stagnation
heating versus velocity (at 56 km) are shown in Figure 3.
Radiational Cooling
This is a form of Boltzmann's Law. The power you can radiate away varies as the
4th power of the surface temperature,
but gets modified for an effective temperature of the surroundings
receiving that radiation (because that gets radiated back, and emissivity is equal to absorptivity):
qrerad,
BTU/hr-ft^2 = e sig (T^4 – TE^4) for T’s in deg R and sig =
0.1714 x 10-8 BTU/hr-ft^2-R^4
For this equation, T
is the material temperature, TE
is the Earthly environment temperature (near 540 R = 300 K), e is the spectrally-averaged emissivity (a
number between 0 and 1), and sig is
Boltzmann’s constant for these customary US units.
This radiation model presumes transparency of
the medium between the radiating object and the surroundings. That assumption fails rapidly above 10
km/s speeds, as the radiating
plasma in the boundary layer about the vehicle becomes more and more
opaque to those wavelengths.
Therefore, do
not attempt radiationally-cooled refractory heat protection designs for entry
speeds exceeding about 10 km/s.
They won't work well (or at all) in practice. Ablative protection becomes pretty much your
only feasible and practical choice.
Heat Conduction Into The Interior
This is a cooling mechanism for the exposed surface, and a heating mechanism for the interior
structure. In effect, you are conducting heat from the high surface
temperature through multiple layers of varying thermal conductivity and
thickness, to the interior at some
suitable "sink" temperature.
The amount of heat flow conducted inward in steady state
depends upon the temperature difference and the effective thermal resistance of
the conduction path. The electrical
analog is quite close, with current
analogous to heat flow rate per unit area,
voltage drop analogous to temperature difference, and resistance analogous to thermal
resistance.
In the electrical analogy to 2-D heat transfer, conductance which is the inverse of
resistance is analogous to a thermal conductance which is a thermal
conductivity divided by a thickness.
Resistances in series sum to an overall effective
resistance, so the effective thermal
resistance is the sum of several inverted thermal conductances, one for each layer. Each resistance sees the
same current, analogous to each thermal
resistance layer seeing the same thermal flux,
at least in the 2-D planar geometry.
Like voltage/effective resistance = current, heat flow per unit area (heat flux) is
temperature drop divided by effective overall thermal resistance. (The geometry effect gets a bit more
complicated than just thickness in cylindrical geometries.) In 2-D:
qcond = (Tsurf - Tsink)/effective
overall thermal resistance
For this the effective overall thermal resistance is the sum
of the individual layer resistances,
each in turn inverted from its thermal conductance form k/t:
eff. th. resistance (2-D planar) = sum by layers of layer
thickness/layer thermal conductivity
Using the electrical analogy, the current (heat flux)
is the voltage pressure (temperature difference) divided by the net effective
resistance (thermal resistance). The
voltage drop (temperature drop) across any one resistive element (layer) is
that element's resistance (layer thermal resistance) multiplied by the current
(heat flux). See Figure 4.
What that says is that for a given layering with different
thicknesses and thermal conductivities,
there will be a calculable heat flux for a given overall temperature
difference. Each layer has its own temperature drop once the heat flux is
known, and the sum of these temperature
drops for all layers is the overall temperature drop.
Any layer with a high thermal resistance will have a
high temperature drop, and vice versa.
High thermal resistance correlates with high thickness, and with low thermal conductivity. A high temperature drop over a short
thickness (a high thermal gradient) requires a very low thermal conductivity
indeed, essentially about like air
itself.
On the other hand, any
high-density material (like the monolithic ceramics) will have high thermal
conductivity, and thus the thermal
gradients it can support are inherently very modest. Such parts trend toward isothermal
behavior. Their high meltpoint does
you little practical good, if there is
no way to hang onto the "cool" end of the part. In point of fact, there may not be much of a “cool” end.
Active Liquid Cooling
In effect, this is
little different than the all-solid heat conduction into a fixed-temperature
heat sink, as described just above. The heat sink temperature becomes the
allowable coolant fluid temperature, and
the last “layer” is the thermal boundary layer between the solid wall and the
bulk coolant fluid. The thermal
conductance of this thermal boundary layer is just its “film coefficient” (or
“heat transfer coefficient”). The simple
inverse of this film coefficient is the thermal resistance of that boundary
layer. See Figure 5.
The main thing to worry about here is the total mass of
coolant mcoolant recirculated,
versus the time integral (for the complete entry event) of the heating
load conducted into it. That heat is
going to raise the temperature of the coolant mass and indirectly the pressure at which it must
operate. That last is to prevent boiling
of the coolant.
∫ qcond dt = mcoolant Cv (Tfinal
– Tinitial) where Tfinal
is the max allowable Tsink
Balancing the Heat Flows: Energy Conservation
A patch of heat shielding area sees convective heating from
air friction, and may see significant
radiation heating if the entry speed is high enough. That same patch can conduct into the
interior, and it can radiate to the
environment, if the adjacent stream
isn't opaque to that radiation. If the
heat shield is an ablative, some of the
heating rate can go into the latent heat of ablation. See Figure 6.
The correlations for convective and radiation stagnation heating
given above depend upon vehicle speed,
not plasma temperature. The
equation for conduction into the interior depends upon the surface and interior
temperatures. Re-radiation to the
environment depends upon the surface and environmental temperatures. Of these,
both the environmental and heat sink temperatures are known fixed
quantities.
If the heat shield is ablative, then the surface temperature is fixed at the
temperature at which the material ablates;
otherwise, surface temperature is
free to "float" for refractory materials that cool by radiation.
The way to achieve energy conservation for refractories is
to adjust the surface temperature until qconv + qrad - qcond
- qrerad = 0. For
ablatives, the surface temperature is
set, and you just solve for the rate of
material ablation (and the recession rate):
qabl = qconv + qrad - qcond
- qrerad.
The heating flux rate qabl that goes into
ablation, divided by the latent heat of
ablation Labl times virgin density ρ, can give you an estimate of
the ablation surface recession rate r (you
will want to convert to more convenient units):
(qabl BTU/ft^2-s)/(Labl BTU/lbm)(ρ lbm/ft^3)
= ft^3/ft^2-s = r, ft/s
(qabl W/m^2)/(Labl W-s/kg)(ρ kg/m^3)
= m^3/m^2-s = r, m/s
Other Locations
Those require the use of empirical correlations or actual
test data to get accurate answers.
However, to just get in the
ballpark, any guess is better than no
guess at all! For lateral windward-side
heating, try about half the heat flux as
exists at the stagnation point. For
lee-side heating in the separated wake,
try about 10-20% of the stagnation heating.
Clarifying Remarks
Bear in mind that these equations are for steady-state
(thermal equilibrium) exposure.
The conduction into the interior is the slowest to respond to
changes. Transient behavior takes
a finite-difference solution to analyze. There is no way around that
situation.
But if that conduction effect is small compared to the
applied heating terms because there is lots of re-radiation or there is lots of
ablation to balance them, you can then approximate
things by deleting the conduction-inward term.
You simply cannot do that if there is no ablation or re-radiation. And your conduction effect will not be
small compared to the heating, if you
are doing active liquid cooling.
If you are entering from Earth orbit at speeds no more than
8 km/s, you can reasonably ignore the
plasma radiation stagnation heating term.
On the other hand, for entry
speeds above 8 km/s, your re-radiation
cooling term will rapidly zero as the plasma layer goes opaque to thermal
radiation. Its transmissibility must
necessarily zero, in order for its
effective emissivity to become large.
The zero transmissibility is what zeroes the re-radiation term.
If you choose to do a transient finite-difference thermal
analysis, what you will find in the
way of temperature distributions within the material layers has little to do
with steady-state linear temperature gradients. Instead,
there will be a “humped” temperature distribution that moves slowly like
a wave through the material layers. This
is called a “thermal wave”. It forms
because heat is being dumped into the material faster than it can percolate
through by conduction. See Figure 7.
Figure 7 – The Thermal Wave Is a Transient Effect
This humped wave of temperature will decrease in height and
spread-out through the thickness, as it
moves through the material. But, usually its peak (even at the backside of
the heat shield) is in excess of the steady-state backside temperature
estimates. It may take longer to
reach the backside than the entire entry event duration, but it will certainly tend to overheat any
bondlines or substrate materials.
Material properties such as thermal conductivity are
actually functions of material temperature.
These are usually input as tables of property versus temperature, into the finite-difference thermal
analyses. Every material will have its
own characteristics and property behavior.
I did not include much material data in this article, in the way of typical data, for you to use. As I said at the beginning, this article is more about “understanding”
than it is “how-to”.
The local heating away from the stagnation point is
lower. There are many correlations for
the various shapes to define this variation,
but for purposes of finding out what “ballpark you are playing in”, you can simply guess that windward lateral
surfaces that see slipstream scrubbing action will be subject to crudely half
the stagnation heating rate. Lateral
leeward surfaces that face a separated wake see no slipstream scrubbing
action. Again, there are lots of different correlations for
the various situations, but something
between about a tenth to a fifth of stagnation heating would be “in the
ballpark”.
Low density ceramics (like shuttle tile and the
fabric-reinforced stuff I made long ago) are made of mineral flakes and fibers
separated by considerable void space around and between them. The void space is how minerals with a high
specific gravity can be made into bulk parts with a low specific gravity:
sgmineral * solid volume fraction = sgmineral
*(1 – void volume fraction) = bulk effective sg
The low effective density confers a low thermal conductivity
because the conduction paths are torturous,
and of limited cross-section from particle to particle, through the material. Such thermal conductivity will be a lot
closer to a mineral wool or even just sea level air, than to a firebrick material.
This low effective density also reduces the material
strength, which must resist the wind
pressures and shearing forces during entry.
A material of porosity sufficient to insulate like “mineral wool-to-air”
will thus be no stronger than a styrofoam.
So, typically, these low density ceramic materials are weak. And they are very brittle. The brittleness does not respond well to stress-
or thermal expansion-induced deflections in the substrate, precisely because brittle materials have
little strain capability. That
fatal mismatch has to be made up in how the material is attached to the
substrate. If bonded, considerable flexibility is required of the
adhesive.
Related Thermal/Structural Articles On This Site
Not all of these relate directly to entry heat
transfer. The most relevant items on the
list are probably the high speed aerodynamics and heat transfer
article, and the article taking a look
at nosetips and leading edges.
The “trick” with Earth orbit entry using refractories
instead of ablatives is to maximize bluntness in order to be able to use low
density ceramics at the stagnation zone without overheating them. That leaves you dead-broadside to the
slipstream, and thus inevitably ripping
off your wings, unless you do something way
“outside the box”.
The pivot wing spaceplane concept article is a
typical “outside the box” study restricted to 8 km/s or less. The older folding wing spaceplane article
is similar. In both studies, the wings are relocated out of the slipstream
during entry, which is conducted dead
broadside to the oncoming flow.
The reinforced low density ceramic material that I made long
ago is described to some extent in the article near the bottom of the list
(about low density non-ablative ceramic heat shields). It is like the original shuttle tile material
that inspired it, but is instead a
heavily reinforced composite analogous to fiberglass. This information was also presented as a paper
at the 2013 Mars Society convention.
The fastest way to access any of these is to use the search
tool left side of this page. Click on the
year, then on the month, then on the title. It is really easy to copy this list to a txt
or docx file, and print it.
1-2-20…On High Speed Aerodynamics and Heat Transfer
4-3-19…Pivot Wing Spaceplane Concept Feasibility
1-9-19…Subsonic Inlet Duct Investigation
1-6-19…A Look At Nosetips (Or Leading Edges)
1-2-19…Thermal Protection Trends for High Speed Atmospheric
Flight
7-4-17…Heat Protection Is the Key to Hypersonic Flight
6-12-17…Shock Impingement Heating Is Very Dangerous
11-17-15…Why Air Is Hot When You Fly Fast
6-13-15…Commentary on Composite-Metal Joints
10-6-13…Building Conformal Propellant Tanks, Etc.
8-4-13…Entry Issues
3-18-13…Low-Density Non-Ablative Ceramic Heat Shields
3-2-13…A Unique Folding-Wing Spaceplane Concept
1-21-13…BOE Entry Analysis of Apollo Returning From the
Moon
1-21-13…BOE Entry Model User’s Guide
7-14-12…Back of the Envelope Entry Model
There are also several studies for reusable Mars landers
that I did not put in the list. They are
similar to the two spaceplane studies,
but entry from Mars orbit is much easier than entry from Earth
orbit. Simple capsule shapes work fine
without stagnation zone overheat for low density ceramics, even for the large ballistic coefficients
inherent with large vehicles.
Final Notes
I’ve been retired for some years now, and I have been retired out of aerospace work
much longer than that. I’ve recently
been helping a friend with his auto repair business, but that won’t last forever.
Not surprisingly, I
am not so familiar with all the latest and greatest heat shield materials, or any of the fancy computer codes, and I have little beyond these
paper-and-pencil-type estimating techniques to offer (which is exactly “how we
did it” when I first entered the workforce long ago). Yet these simple methods are precisely what
is needed to decide upon what to expend the effort of running computer
codes! Today’s fresh-from-school
graduates do not know these older methods.
But I do.
Sustained high speed atmospheric flight is quite distinct
from atmospheric entry from orbit (or faster),
but if you looked at that high speed aerodynamics and heat transfer article
cited in the list, then you already know
that I can help in that area as well.
Regardless, it should
be clear that I do know what to worry about as regards entry heat protection, and how to get into the ballpark (or
not) with a given design concept or approach in either area (transient entry or
sustained hypersonic atmospheric flight)!
I can help you more quickly screen out the ideas that won’t work, from those that might.
And if you look around on this site, you will find out that I also know enough to
consult in ramjet and solid rocket propulsion,
among many other things. I’m
pretty knowledgeable at alternative fuels in piston and turbine engines, too.
If I can help you,
please do contact me. I do consult in these things, and more.
More? More: I also build and sell cactus eradication farm
implements that really work easier,
better, and cheaper than anything
else known. I turned an accidental
discovery into a very practical family of implements. It’s all “school of hard knocks” stuff.