More-Refined 1- vs 2-Stage to LEO

Because of repeated questions from knowledgeable readers,  I took a more refined look at the scenario of chemical launch to eastward LEO at low inclination,  using either an expendable two-stage to orbit design (TSTO),  or an expendable single-stage-to-orbit design (SSTO).  For this more refined look,   I added delta-vee (dV) budgets for rendezvous and deorbit,  I looked at a more representative orbital speed requirement,  and I let the second stage of a TSTO shoulder a minority of the gravity loss (the split being arbitrary).  The first stage shoulders all the drag loss.  The SSTO shoulders all of both losses.  See Figure 1. 

Figure 1 – Revised dV Requirements That Are More Realistic

The 75-25 split on shouldering gravity losses is arbitrary,  but “in the ballpark”.  I still picked 5% each for gravity and drag losses,  the basis being the kinetic energy-equivalent surface circular orbit speed.  5% gravity loss would go with good kinematics off the launch pad,  meaning 0.5 gee above gravity or better,  or a thrust/weight of 1.5 or better at launch.  5% drag loss would go with a clean,  slender shape,  really meaning a length/diameter ratio of 6 or larger,  with no steps in diameter. 

               TSTO Design Considerations

For the TSTO,  what I presumed was LOX-RP1 propulsion in the first stage,  “compromise”-sized to improve the ascent-averaged specific impulse (Isp),  such that the engine is just barely unseparated firing at sea level,  at 85% of max chamber pressure Pc.   I presumed LOX-LH2 propulsion in the second stage,  sized at an expansion area ratio (A/A*) = 100,  to limit engine length. 

Both the first and second stage engine technologies were presumed to be modest technologies that do not push the state of the art (SOTA) very hard,  something that lowers development costs that must be amortized over the launches to be made.  Accordingly,  I presumed only a max Pc = 2500 psia,  and that whatever cycle it is has,  has a dumped bleed fraction of 2%.  The pressure turndown ratio (P-TDR) for throttling is only 2.5.   The usual curved bell of 18-and-8-degree profile is presumed,  along with a throat area discharge coefficient C_D = 0.995. 

Rather modest stage structural design technologies were also presumed,  such that both loaded-stage inerts were 5% of stage ignition mass,  again to reduce development costs that must be amortized over the launches to be made.  4% has been demonstrated,  but requires custom alloys,  even for expendables.  The definitions are such that payload fraction plus inert fraction plus propellant fraction sum to 1.  The first stage payload is the fully-loaded second stage,  and the second stage payload is a fixed 100 metric ton mass riding out in the open,  atop the second stage.

All propulsion was initially sized for a thrust requirement of 500,000 lb (226.76 metric tons-force,  2223.7 KN).  For any ascent engine,  this was imposed at sea level.  For the TSTO second stage,  this was imposed in vacuum.  Performance was computed vs altitude,  and those values averaged over the list of altitudes in the altitude table. 

That is not exactly correct for an “ascent-averaged Isp”,  because the vehicle does not spend equal time at all these altitudes,  but it is well within the “ballpark”.  I compensated for any error by presuming an Isp about 2-5 s below what the sizing calculation said.  Dimensions and flow rates depend upon sized thrust.  Flow rates and cross sectional areas scale in proportion to thrust,  while linear dimensions scale in proportion to the square root of thrust.  Isp does not scale.

The TSTO first stage sea level engine sizing to 500,000 lb thrust is shown in Figure 2.  The TSTO second stage vacuum engine sizing to 500,000 lb thrust is shown in Figure 3.  

Figure 2 – As-Sized TSTO First-Stage Engine Data,  Un-Rescaled

Figure 3 – As-Sized TSTO Second-Stage Engine Data,  Un-Rescaled

               SSTO Design Considerations

For the SSTO,  I looked at both LOX-LCH4 propulsion and LOX-LH2 propulsion.  Such engines were “compromise”-sized for better ascent-averaged Isp,  just like the first stage engines in the TSTO design.  However,  the technology baseline presumed,  pushes the SOTA very hard indeed:  these designs presume a max Pc = 4000 psia,  a cycle such that the dumped bleed fraction BF = 0,  and a more challenging P-TDR = 3.  (They would compare to the SpaceX Raptor designs.)

I kept the same rather modest stage structural design technology,  with a stage inert fraction of 5%.  In this case,  there is only one stage,  and its 100 metric ton payload rides out in the open,  atop the stage,  exactly the same as was presumed for the TSTO. 

The hydrogen-fueled version looked good enough to check the effects of just modest-technology.  That would use the LOX-LH2 propellant ballistic models,  but employ the same reduced Pc and non-zero-BF that was used for the TSTO engine designs.  The methane-fueled version had a low-enough payload fraction to warrant skipping this look.

Figure 4 shows the un-rescaled methane engine results for the edge-of-the-SOTA.  Figure 5 shows the un-rescaled hydrogen engine results for the edge-of-the-SOTA.  Figure 6 shows an un-rescaled hydrogen design of the same modest-technology parameters as were used in the TSTO design.  

Figure 4 – As-Sized SSTO Methane Engine,  Edge-of-the-SOTA,  Un-Rescaled

Figure 5 – As-Sized Hydrogen Engine,  Edge-of-the-SOTA,  Un-Rescaled

Figure 6 – As-Sized Hydrogen Engine,  modest SOTA,  Un-Rescaled

               Doing More Detail

In my previous posting on this topic,  “Launch to Low Earth Orbit:  1 Or 2 Stages?”,  posted 3 March 2024,  all I did was convert dV’s to mass ratios MR,  turn that into a list of mass fractions,  and then size a weight statement from a fixed payload mass.  I used the stage ignition masses to size total thrust requirements.  And that was it. 

I have since added to the simple spreadsheets I used for that analysis.  If you look at the stage overall thrust requirements and masses to be accelerated,  you can choose a number of engines appropriate for that stage,  and thus from that overall thrust requirement,  determine what those individual engine thrust ratings must be. 

I created a little thrust-resize spreadsheet,  which takes the as-sized engine data,  and rescales them to the necessary thrust rating.  Areas and flow rates scale as proportional to thrust,  while dimensions scale as proportional to the square root of thrust.  What is important is the estimated overall dimensions of an individual engine.  Part of Figure 7 illustrates how these engine dimensions are scaled and created from the estimated engine sizing data.

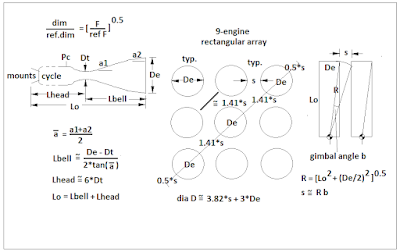
For only a 9-engine cluster,  I worked out how to use the engine dimensions and an assumed max gimbal angle to estimate a clearance spacing between engine bells so that gimballing one will avoid impacting an adjacent bell.   Adding this up along a diagonal of the 9-engine cluster provides an estimate of the min stage diameter,  as is also shown in Figure 7.  I used 15 degrees for the max gimbal angle,  an arbitrary choice.

Figure 7 – How Engine Dimensions Determine Stage Diameter

Once you have a min stage diameter estimate,  you can begin to approximate the lengths of the tanks,  engine bays,  and interstages.  Those lead to a vehicle length/diameter ratio estimate,  from which to judge whether the “slender” assumption justifying lower drag loss was justified.  This is based on the same diameter for the whole vehicle,  to also qualify as “clean”,  for justifying the lower drag loss assumption.

You can use an estimate of the engine’s operating r-ratio to split total propellant mass into oxidizer and fuel masses,  in each stage.  You can use the standard specific gravity values for those propellant materials to turn those oxidizer and fuel masses into volumes (specific gravity is numerically equal to density in metric tons per cubic meter).  Dividing volume by base area gets you a length of the tank that is an underestimate,  since there are curved pressure dome heads.  Compensate by assuming an inter-tank length of about a diameter. 

First stage (or single stage) estimated engine length is the length of the first stage engine bay (if there is one),  but is part of the overall first stage length regardless.  If there is a second stage,  there is some sort of interstage between it and the first stage,  whose length is the estimated overall length of a second stage engine.   The length of the payload is arbitrarily assumed to be 2 diameters.

The resulting augmented spreadsheet image for the TSTO design is shown in Figure 8.  The leftmost block is the original mass and thrust sizing calculations.  The rest is what I added to determine engine counts and thrusts,  and to use the re-scaled engine dimensions to do the volumes and lengths.   Images of the rescaled kerosene and hydrogen engine spreadsheets were not included,  but are reflected in the dimensional data input at top right. 

Figure 8 – Spreadsheet Image For TSTO Detail Sizing

A somewhat similar-looking spreadsheet was used for the SSTO designs,  starting with the LOX-LCH4 design looked at initially in the earlier posting.  That produces the detail sizing spreadsheet image of Figure 9,  and the associated engine re-scale spreadsheet image of Figure 10. 

Figure 9 – Spreadsheet Image For SSTO Detail Sizing,  Methane,  Edge-of-SOTA

Figure 10 – Spreadsheet Image For SSTO Engine Re-Scale,  Methane,  Edge-of-SOTA

The reader should be aware of one disconnect here:  I picked 15 engines,  not 9!  The stage diameter estimate is wrong:  it is too small!  That lowers the vehicle L/D ratio even further,  from the too-low value already obtained.  For this design,  the drag dV loss to cover should have been more than the 5% used in the velocity requirements analysis shown in Figure 1 above. 

So as it turns out,  the recommendation in the earlier posting to use the LOX-LCH4 propellant combination for the SSTO design has been shown to be wrong!  This also shows up in the 2.1% payload fraction and the enormous 4850 metric ton ignition mass,  given in Figure 9 above.

Accordingly,  I did another edge-of-SOTA design for the SSTO,  this time using LOX-LH2 propulsion.  The image of the detail sizing spreadsheet is given in Figure 11.  The engine dimension re-scaling is shown in Figure 12.  This one actually uses 9 engines,  so the diameter is “right”,  and so is the L/D.

Figure 11 -- Spreadsheet Image For SSTO Detail Sizing,  Hydrogen,  Edge-of-SOTA

Figure 12 -- Spreadsheet Image For SSTO Engine Re-Scale,  Hydrogen,  Edge-of-SOTA

Comparing the payload fractions and ignition masses between Figures 8 and 11,  7.5% and 1401 tons TSTO vs 7.5% and 1325 tons SSTO,  we see pretty much equivalent performance between the TSTO using LOX-RP1 and LOX-LH2 both at modest engine SOTA,  and the SSTO using all-LOX-LH2,  but at the edge of the engine SOTA.  Clearly the higher average ascent Isp of the hydrogen vs the methane made a huge difference for the SSTO,  more than I initially expected to see!

That brings up determining the effects of pushing the engine SOTA so hard with the SSTO engines.  To determine that,  I used the modest SOTA hydrogen ascent engine data of Figure 6 above,  to create yet another SSTO design sizing,  by these same methods.  The detail sizing spreadsheet image is given in Figure 13,  with the engine re-scale data in Figure 14.  

Figure 13 -- Spreadsheet Image For SSTO Detail Sizing,  Hydrogen,  Modest SOTA

Figure 14 -- Spreadsheet Image For SSTO Engine Re-Scale,  Hydrogen,  Modest SOTA

This one is not that much reduced in payload capability (6.7% vs 7.5% for the Edge-of-SOTA SSTO and the TSTO).  It increased its launch mass a little,  being 1487 metric tons,  vs 1325 for the edge-of-SOTA SSTO and 1401 for the TSTO.  Yet they are all 3 in the same basic class of vehicle sizes.  I did select 9 engines,  so the diameter is valid,  and the L/D is “good”.  There is no reason the more modest hydrogen engine technology might not serve,  and serve well.

               Results and Conclusions

Sketched images for the TSTO with modest-technology kerosene and hydrogen propulsion,  the SSTO with SOTA methane propulsion,  the SSTO with SOTA hydrogen propulsion,  and the SSTO with modest-technology hydrogen propulsion,  are given in Figures 15 through 18 below,  respectively.   

As the table above indicates,  it is ascent-averaged Isp that is the critical factor here with the SSTO.  The big gulf between the methane and hydrogen/SOTA ascent-averaged Isp’s corresponds to the big gulf between the payload fractions and the ignition masses.  The small gap between the hydrogen/modest and hydrogen/SOTA Isp’s corresponds to the small gap between payload fractions and ignition masses. 

Changing the propellant combination had a huge effect on ascent-averaged Isp and the resulting sized designs.  Changing how hard the hydrogen engine technology pushes the SOTA did not have a large effect,  only a smaller one.  The sized design reflects exactly that.  See also Figure 19 below. 

Before I ran this more detailed design study,  I thought that pushing the SOTA vs a modest technology would have more of an effect than it actually did.  Now we see:  the propellant combination has the far stronger effect.  Go ahead and use the more modest engine technology.  That will not stop you from doing rather well as an SSTO,  as long as you use LOX-LH2.

The hydrogen upper stage TSTO with modest engine technology is only a little better in terms of payload fraction than the hydrogen SSTO with modest engine technology.  But,  it does offer an easier path to partial reusability,  by substituting a larger lower stage with the ability to fly back and land.  That is something to consider. 

The “compromise” expansion sizing approach for ascent engines is very important,  as that is how one achieves ascent-averaged Isp values higher than an ordinary sea level design.

That sort of “ascent-averaged Isp is dominant” outcome for the SSTO makes me wonder if we could do better than a kerosene first stage for the TSTO.  While beyond scope here,  I will look at that in a future update or posting.  The candidates are methane and hydrogen,  of course.  These will be restricted to “modest engine technology”.  The same methods will be used,  as were used here.  

I do expect that one or both will significantly exceed what we can do with a modest-technology hydrogen SSTO.  The problem will be the same volume issues that afflicted the SOTA-technology methane SSTO.  But we will not know,  until we try. 

Figure 15 – Image of Detailed Results for TSTO,  Modest Kerosene and Hydrogen

Figure 16 – Image of Detailed Results for SSTO,  SOTA Methane

Figure 17 – Image of Detailed Results for SSTO,  SOTA Hydrogen

Figure 18 – Image of Detailed Results for SSTO,  Modest Hydrogen

Figure 19 – Plots Showing Relative Effect of Engine Technology Level and Propellant Combination

-----

Update 3-12-2024:

I carried out the plan outlined at the end of the article above,  to investigate two higher-performing propellants in the TSTO.  That required sizing a LOX-LCH4 engine of modest technology to be an ascent engine in the first stage.  I already had a LOX-LH2 ascent engine sized,  of modest technology,  investigated for the SSTO.  These were both resized to fit a 9 engine cluster of the necessary thrust,  just as in the studies done in the article above,  with the updated vehicle sizing. 

For these changes to the TSTO,  I did not change its second stage at all.  It was,  and still is,  powered by two small LOX-LH2 engines of modest technology,  sized as vacuum engines with A/A* = 100,  just as before.  The resized modest-technology methane ascent engine is illustrated in Figure 20 below.  The sized TSTO vehicle with that set of modest technology methane engines in its first stage is depicted in Figures 21 and 22 below. The sized TSTO vehicle with a set of modest technology hydrogen engines in its first stage is depicted in Figures 23 and 24 below. 

I did not see much difference between the kerosene and methane first stage TSTO vehicles in terms of payload fraction,  but the ignition weight did reduce somewhat,  going to methane.  A part of this is the reduced thrust requirement reducing engine lengths,  in a vehicle whose length and diameter are primarily sensitive to engine dimensions and number.  With a hydrogen first stage,  the payload fraction increased noticeably,  and the launch weight decreased significantly further. 

I had not reduced the ascent-average Isp of the modest technology hydrogen ascent engines by 2-5 s when I did the hydrogen TSTO in the article above,  inputting 447 s to the vehicle sizing.  Here,  I did,  inputting 445 s Isp to the vehicle sizing. I ignored this small difference making the comparison plots of trends with the two vehicles,  which is Figure 25 below.  The main takeaway is the lower slopes of the trends with the TSTO,  compared to the steep slopes of the trends for the SSTO. 

There is a good,  simple reason for that:  the TSTO second stage is vacuum hydrogen-powered,  and shoulders the majority of the dV requirement imposed on the vehicle.   That makes the first stage mass ratios rather small in comparison,  where the added benefit of higher first-stage Isp is “diluted” by the constant-second stage effects.  In contrast,  the SSTO has to get all the dV requirement out of its single stage.  The benefits of the higher Isp are entirely undiluted by anything,  hence the effects are large,  and the trend slopes are steep.

Figure 20 – Sized Methane Ascent Engine of Modest Technology

Figure 21 – Vehicle Sizing Data for Modest-Technology Methane Engines in the First Stage

Figure 22 – Vehicle Sketch for Modest-Technology Methane Engines in the First Stage

Figure 23 – Vehicle Sizing Data for Modest-Technology Hydrogen Engines in the First Stage

Figure 24 – Vehicle Sketch for Modest-Technology Hydrogen Engines in the First Stage

Figure 25 – Comparison Plots of Trends,  With All Vehicles

               Conclusions

The results here are for all-expendable vehicle sizings.  The conclusions apply to the same,  with exceptions for re-usability as stated in notes 7 and 8. 

#1. If you design a TSTO expendable “from scratch” for delivering large payloads to LEO,  always use a LOX-LH2 engine designed for vacuum operation to power the second stage. 

#2. If you design a TSTO expendable “from scratch” for delivering large payloads to LEO,   it does not matter very much which of the 3 propellant combinations you use for powering the first stage.  The trends favor LOX-LH2,  but these trends are weak (low slope).  LOX-RP1 and LOX-CH4 also serve well.

#3. Whether you design “from scratch” a TSTO expendable or an SSTO expendable for delivering large payloads to LEO,   use “ascent engines” with their expansion ratio designed as an ascent compromise:  just barely unseparated,  at around 85% max Pc,  at sea level.  Engines designed in this way will have a higher ascent-averaged Isp than traditional sea level engine designs,  which are generally perfectly expanded to sea level pressure at max Pc.  And the actual flight configurations  are testable at sea level in the open-air nozzle mode,  which helps to greatly lower development costs that must be amortized,  and to greatly lower development risks. 

#4. If you design “from scratch” an SSTO expendable for delivering large payloads to LEO,  go for the LOX-LH2 propulsion.  Because of the steep trends,  these designs are critically-sensitive to ascent-averaged Isp above all other considerations.  Only LOX-LH2 provides high enough Isp.

#5. Neither type of vehicle is extremely-sensitive to how hard the engine technology pushes the SOTA,  because the Isp difference is not all that large between high-SOTA and rather modest technology,  something true for all 3 propellant combinations.   With the more modest technology,  development risks and efforts are lower,  leading to lower development costs to be amortized.

#6. I did not evaluate the impact of stage structural design technology!  I got good results from the best of the designs at a rather modest stage inert mass fraction assumption:  5% inert in every loaded stage.  4% has been demonstrated,  but I deliberately chose not to push those limits!  The less demanding structural design lowers development effort levels and development risks,  thus lowering the development costs to be amortized.

#7. The TSTO offers a fairly easy path to partial re-usability,  by enlarging the first stage design to enable its flyback,  entry,  and recovery.  This is primarily enabled by the relatively-low (only supersonic) speeds at entry,  in turn imposed by the relatively low staging speed,  which also lowers the burn-back dV requirement.

#8. The SSTO does not offer an easy path to re-usability,  because the entry speeds are orbital-class hypersonic,  and the stage simply does not have the inert fraction to permit the design changes to make it into a survivable entry vehicle at all,  much less to land.  The “proof” is in the negative:  if this were not true as stated,  it would have already been done,  routinely,  along with first stage recoveries.

               Final remarks

Do not take these “designs” as ready-to-build!  While the engine ballistics and performance estimates are rather good,  the weight statements are less so,  and the dimensional estimates are only “ballpark”.   It is the trends that should be used to support real design candidate screening and selections.  Some of that screening I have done for you,  in this article. 

To address questions from knowledgeable readers,  I made the dV requirements more representative of vehicles that can get to orbit and rendezvous with a destination,  plus a deorbit capability for proper disposal.  But,  there are a lot of things that I did not address.

I did not address propellant ullage / engine relight issues,  and I did not address the unrecoverable propellant fractions that are inherent with any type of tank design.  Further,  I did not address the actual end dome shapes or designs of the liquid propellant tanks,  or the possibility of a common dome design,  which can be done with some propellant combinations,  but by no means all of them. 

These are not only “from scratch” vehicle ballpark design sizings,  they are also “from scratch” paper engine design sizings,  a start-point only for a real engine design and development effort.  I made absolutely no attempt in this work,  to use any pre-existing engine designs of any kind at all!   

My work here can be re-scaled to other delivered payload masses (the 100 metric tons that I used here was an arbitrary number),  so that the trends I uncovered can help guide real concept selection and real design efforts for other-size projects done by others.  If a pre-existing engine of the right propellant combination fits your design project,  so much the better!  Any development costs you can avoid are one less thing to amortize over the life of the product.  

Launch to Low Earth Orbit: Fixed-Geometry Options

The question keeps coming up among enthusiasts about how fixed-geometry conventional bell-type rocket engines cannot adequately serve for ascent through the atmosphere.  This “justifies” adding technologies such as bell extensions or free-expansion nozzle designs.  This document addresses what can be done with a fixed-geometry expansion bell,  if you carefully design it for that ascent purpose,  and subject to the constraint that you can test the flight article at sea level,  open-air nozzle conditions,  for both cost-effectiveness,  and for testing the actual flight article. 

For this study,  I presumed liquid oxygen/liquid hydrogen (LOX-LH2) propellants,  and a modest engine design technology characterized as max chamber pressure (Pc) 2500 psia,  with a pressure turndown ratio (P-TDR) of 2.5.  Expansion bells are curved,  with an “18-8” degree profile,  for a constant nozzle kinetic energy efficiency (η_KE) just over 98.7%.  Throat discharge coefficient was also constant at C_D = 0.995.  The engine cycle is modeled as “modest modern technology” with a bleed dump fraction (BF) of 2%.  All these variables were held exactly the same,  for the 3 designs explored here,  to investigate the effects of expansion and thrust sizing effects.

I explored 3 designs:  (1) a conventional “sea level-optimized” design,  (2) a typical conventional “vacuum optimized” design,  and (3) the practical compromise design that I favor for best ascent performance.  The sea level “optimization” requires that the bell expansion be sized for max chamber pressure expanding down to standard sea level pressure,  and with throat and exit dimensions (and total flow rate) sized so that sea level thrust at max Pc is a required value. 

There is really no such thing as a “vacuum-optimized” expansion bell!  Such would have an infinite exit area expanding the flow to exactly zero exit plane pressure,  which is utter nonsense.  Vacuum engine bell designs are not optimized in any way,  they are merely constrained by practical design constraints.  The word “optimized”,  while routinely used,  is a complete misnomer for such things.

The length and diameter of the bell has to fit practical dimensional constraints so that the engine will fit within the available space at the rear end of the stage,  often even more severely constrained than one might think,  if the engine must gimbal for thrust vectoring.  For purposes of this study,  I simply analyzed to a convenient “typical” approximation:  a nozzle area expansion ratio of 100.  These cannot be fired open-air nozzle at sea level,  even at full throttle.  Higher Pc lowers the separation altitude,  but does not eliminate the sea level separation problem.

My preferred sizing approach defines a high part-throttle setting at which the bell expands from the part-throttle Pc to an over-expanded exit plane pressure Pe that corresponds to being on the verge of backpressure-induced flow separation at sea level.  This allows sea level open-air nozzle testing of the full flight configuration at that part-throttle setting or higher,  a considerable cost savings in development testing!  Such designs are over-expanded,  and thus underperform the sea level designs at sea level.  But,  they also offer considerably more expansion ratio,  and so perform nearly as well as the so-called “vacuum optimized” designs,  out in vacuum.  It’s a compromise for ascent!

For such a compromise design to serve in ascent,  I size its dimensions and flow rate to meet the imposed thrust requirement at sea level.  (For “vacuum optimized” designs that can still be tested at sea level,  I size the dimensions and flow rates to a thrust requirement imposed out in vacuum;  that was not done for this study.) 

The normal approach to “vacuum-optimized” designs results in larger expansion ratios that simply cannot be tested at sea level open-air nozzle at all!  The only feasible way to test them open-air at sea level,  is to fit them with shorter test bells that do not flow-separate.  You cannot surface-test the full flight article that way,  but that is what is often done,  anyway.

               Sea Level Design

The sea level design is depicted in Figure 1.  Expansion was from max Pc to Pe = sea level standard pressure.  Thrust was sized to a 500,000 lb (226.7 metric tons-force,  2223.7 KN) requirement imposed at sea level,  full throttle conditions.  I used my “compressible.xlsx” spreadsheet tool for this effort,  specifically the “r noz alt” worksheet so that performance versus altitude could be plotted,  and ascent-averaged.   Selected items from the spreadsheet were copied to the figure,  along with the two plots the worksheet creates.  These were annotated as shown.  Note how the sea level design can be tested open-air nozzle at sea level,  even at the minimum throttle setting.  Thrust in vacuum is only a little higher than sea level.  Vacuum specific impulse (Isp) is much higher than the sea level value,  but the ascent-averaged Isp is only a little lower than the vacuum value.

Figure 1 – Standard Sea Level Design,  As Is Often Used In First Stages for Ascent

               Typical of Standard “Vacuum-Optimized” Designs

This design is depicted in a very similar format in Figure 2.  Expansion was sized from max Pc to a Pe that produced A/A* = 100.  Dimensions and flow rates were sized from a thrust requirement imposed in vacuum.  This was the same 500,000 lb (226.7 metric tons-force,  2223.7 KN).  The vacuum performance is quite good,  as one would expect.  This design cannot be used for ascent,  or tested open-air nozzle at sea level,  because it suffers backpressure-induced flow separation at all throttle settings.  The nozzle is separated below about 20 kft at 100% Pc,  separated below about 25 kft at 85% Pc,  and separated below about 40 kft at the min setting of 40% Pc.  The as-sized dimensions and flow rate are different from those of the sea level design,  but not very much different at all!  A common chamber power head could be used with two different bells,  by just adjusting one thrust requirement a little bit.  That was not done here,  though.

Figure 2 – Typical of Standard “Vacuum-Optimized” Designs,  Cannot Be Used for Ascent

               Compromise Design Intended For Ascent Use

This design is depicted in Figure 3,  using a format very similar to the other two designs.  The expansion was sized for 85% Pc down to a Pe = 3.63 psia that had just barely above standard sea level pressure as its flow separation backpressure.  This is overexpanded,  as much as can be tolerated at that throttle setting,  without actually separating. That produces a bigger area expansion ratio than a sea level design,  while still less than most “vacuum-optimized” designs. 

Being intended for ascent use,  I imposed the thrust requirement at sea level,  as the same 500,000 lb (226.7 metric tons-force,  2223.7 KN).  Both this and the standard sea level design meet this thrust requirement at sea level and 100% throttle.  The compromise design thrusts better out in vacuum than the sea level design,  at about 587,000 lb,  versus only about 531,000 lb.  The “vacuum-optimized” design delivers 500,000 lb in vacuum,  exactly per its design. 

The real story is in terms of Isp.  The compromise design is overexpanded and has lower Isp at sea level than the sea level design.  However,  its vacuum performance is only a little bit less than that of the so-called “vacuum-optimized “ design,  which cannot be used at sea level at all!  Further,  its ascent-averaged Isp is actually greater than that of the sea level design.  The compromise design can be used for ascent from sea level to vacuum,  with better ascent-averaged Isp than the sea level design,  and nearly the vacuum Isp of the “vacuum-optimized” design!  And it does this with the same high thrust/weight ratio,  and fewer potential failure modes,  as are inherent in all fixed geometry bell designs.  Further,  it is testable at sea level in open-air nozzle mode,  and in the full flight configuration,  a real plus!

Figure 3 – Compromise Design Intended For Ascent Use

               Summary Comparison

The table shows a summary comparison of the 3 designs.  All this was in the figures in more detail.

Discussion of Other Design Alternatives

There are two design alternatives to the fixed-geometry expansion bell:  (1) the extendible bell extension,  and (2) the free-expansion approach. 

The extendible bell extension is depicted in Figure 4,  which I got from R. Gregory Clark’s “Polymath” site “exoscentist.blogspot.com”.  Basically,  the idea is to add the bell extension hardware to a sea level design,  which converts it to a “vacuum-optimized” design geometry with the same chamber power head.  You would extend the bell section somewhere above the altitude at which the vacuum geometry risks flow separation,  something subject to some design optimization,  of course.  But,  that would always occur somewhere in the lower stratosphere,  in any event,  as can be seen by the curves in Figure 2 above,  which have a definite “knee” somewhere near 50 kft altitude. 

Figure 4 – Depiction of the Extendible Bell Extension Concept – From R G Clark’s “Polymath” Site

This approach will indeed increase the ascent-averaged Isp,  to something between the vacuum design value and the sea level design value,  and likely much closer to the vacuum value,  as we have already seen.  But,  besides imposing geometric restrictions upon the shape and placement of the chamber power head and plumbing items,  adding this kind of hardware is going to increase engine inert mass!  

You will see this as a substantially-lower engine thrust/weight ratio compared to simpler fixed-geometry designs.  That will adversely-affect stage or vehicle inert masses,  and thus also mass ratio and velocity-increment capabilities.  You will not see as much (if any) improvement over the compromise design,  as otherwise only the ascent-averaged Isp might suggest.

Further,  adding moving hardware with sealing issues adds a long list of potential failure modes to the list of potential failure modes that any rocket engine has.  This is a safety/reliability thing,  something not so easily quantified,  but very real,  nonetheless!  I have no numbers to show,  but I do have to ask the very pertinent question:  why would you do this,  unless you were absolutely forced into taking the increased risks?

The free-expansion nozzle design approach is something I have explored in other articles on this site.  It can take many forms,  but the best-known is the aerospike nozzle approach.  This can be a coaxial or a 2-D linear design.  The 2-D linear design was intended to be implemented on the X-30 “Venture Star” design,  for one-stage low orbit access,  that ultimately proved unsuccessful for a variety of reasons.  Most of those had to do with losing strength by reducing inert weight too far.

These free-expansion designs all suffer from a common problem:  as the ambient atmospheric pressure drops to low or zero values,  the streamlines of the propulsion stream diverge excessively and very adversely,  in terms of critically-low effective kinetic energy efficiency.  This drastically reduces specific impulse (Isp) at high altitudes and on out into vacuum,  and it is inherent,  being fundamental compressible flow physics!  These things work better than conventional nozzles from the surface out to the lower stratosphere,  but from there on up,  Isp performance falls very drastically out into vacuum.  They are absolutely lousy as vacuum engines,  and they inherently always will be,  despite the common false perceptions to the contrary! 

With the fixed-bell designs showing ascent-averaged Isp closer to the vacuum value than the sea level value,  it is to be reasonably expected that aerospike ascent-averaged Isp will be closer to the utterly-lousy vacuum Isp levels that these designs produce.  Even if not,  the huge deficit the lousy vacuum performance represents,  will drag the ascent-averaged Isp down catastrophically,  no matter how it is computed.

The earlier articles on this site that explore free-expansion nozzle performance are listed below.  Use the blog archive gadget on the left of this page to find them very quickly.  All you need is the title and the date.  Click on the year,  then the month,  then the title if more than one article was posted that month.

Rocket Nozzle Types (bells and aerospikes)      4 February 2023

How Propulsion Nozzles Work                               12 November 2018

Addendum

The “compressible.xlsx” spreadsheet was put together to support a course I created in the basics of compressible flow applications.  Rocket nozzles are but one application of this.  There are multiple worksheets in that spreadsheet file,  of which only three relate to estimating rocket engine performance. 

One (“prop comb”) is just a data library of supporting ballistics data for several propellant combinations.  Another one (“rocket noz”) does the basic sizing calculations with sea level and vacuum estimates versus 3 engine power settings,  and is the same as the one that is also provided for the “orbit basics+” course series.  The third one (“r noz alt”) is the same as “rocket noz”,  but with an additional calculation block of thrust and specific impulse vs altitudes from sea level to vacuum.  This is for the 3 power settings,  and it creates a couple of plots.  There are no inputs,  it is automatic.

Figure 5 depicts an image of the basic calculation block that is in both “rocket noz” and “r noz alt”.  User inputs are highlighted yellow,  and significant results highlighted blue.  There are two other inputs that you must deal with,  after putting the basics into the main input block. 

One of these is the design chamber pressure Pc value for sizing the expansion ratio,  and it is not necessarily the max value.  It works with the exit plane expanded pressure Pe to size the nozzle expansion ratio A/A*.  If you are designing to a fixed expansion,  vary Pe iteratively to obtain the desired value of A/A*.  If instead you are designing to an incipient nozzle separation situation at one of the power settings,  iteratively set Pe until you get the desired separation backpressure Psep in that cell for that power setting (this Psep is usually just barely above standard sea level pressure).

The other is the appropriate thrust coefficient (sea level C_F or out-in-vacuum C_Fvac) from the sized expansion,  to use with the thrust requirement input for sizing dimensions and flow rates.  This determines whether you size to that thrust level at sea level or in vacuum.  The rest is automatic.

Figure 5 – Basic Calculation Block In Both “rocket noz” and “r noz alt” Worksheets

The altitude calculation block that is only included in the “r noz alt” worksheet is depicted in Figure 6.  The first 3 columns show altitude in 1000’s of feet (kft),  the ambient pressure ratio to standard sea level pressure,  and the ambient pressure Pa in psia.  Pa is set to zero at 300 kft (about 90 km) to represent vacuum.  There’s a group of columns for each of the input power settings,  in which the vacuum thrust is corrected to thrust-at-that-altitude with F = Fvac – Pa*Ae,  and the Isp computed from F and the total flow rate at that power setting.  The separation backpressure is also computed for that power setting. 

The user is cautioned to look at the separation backpressure levels and compare those to the ambient pressures at altitude.  Wherever the ambient pressure exceeds the separation backpressure,  the bell will separate at that altitude and power setting.  The plots are generated without regard to separation.  There will be a critical altitude below which separation occurs,  if it occurs at all.  That “trigger altitude” will be different for each power setting. 

Each power setting’s specific impulse values are summed and then divided by the number of entries in the table.  This is an approximation-only to the true ascent-averaged specific impulse at that power setting,  but it is “in the ballpark”.  Doing it this way ignores the fact that the vehicle does not spend equal times at each altitude.  This is partly made up for,  by there being denser points at lower altitudes.    

Figure 6 – The Altitude Calculation Block Only In “r noz alt”  Supporting Plots vs Altitude

If you want a copy of this spreadsheet file,  please contact me.  There is no user manual for it,  though.  This article is probably user manual-enough.

Update 3-5-2024 for -- Launch to Low Earth Orbit:  Fixed-Geometry Options

In looking at what I posted,  I noticed an error and two lacks.  The error was indicating a 2000 psia max Pc in the figures depicting the engines,  when what I actually used was 2500 psia as the max Pc.  That has been corrected in the versions of those figures included below. 

The two lacks were (1) not including the sizes of the engines in the figures,  and (2) not looking at even higher vacuum design exit area ratios A/A* than the 100 that was in the article as originally posted.  Both lacks have been fixed with this update.  I added A/A* = 150 and 200 as Figures 2B and 2C,  and to the comparison table.  Plus,  I included bell exit diameters and estimated lengths (throat to exit) in the comparison table,  now included as Figure 4 in this update.  I also further annotated that comparison table. 

Bear in mind that all of these designs share the same modest-modern technology design characteristics:  max Pc = 2500 psia,  pressure turndown ratio in throttling is 2.5:1,  for 40% min pressure = 1000 psia,  a 2% dumped bleed fraction,  an 18-8-degree curved bell profile,  and a nozzle throat discharge efficiency of 99.5%.   They are all “paper” oxygen-hydrogen (LOX-LH2) engines.  They do not push the state-of-the-art very hard! 

Figure 1 below is the same as Figure 1 in the original article above,  except that I corrected the error reporting max Pc,  and I added bell length.  This sea level design sizes its expansion between 2500 psia Pc,  and 14.696 psia Pe = Pa at sea level.  The dimensions and flow rates size for 500,000 lb of thrust delivered at sea level.  It is neither over-expanded nor under-expanded.  It is “perfectly expanded”,  as any real “sea level design” actually is.

Figure 2 below is the same as Figure 2 in the original article above,  except that I corrected the error reporting max Pc,  and I added bell length.  This is a “vacuum design” sized to an arbitrary A/A* = 100.  The dimensions and flow rates size for an imposed vacuum thrust requirement of 500,000 lb.  Under- or over-expandedness at sea level is irrelevant,  since this design is separated at sea level,  at any throttle setting.  It cannot be used for ascent,  except as an upper stage engine used only essentially exoatmospherically. 

Figure 2B below is the same as the corrected Figure 2 reported here in every way,  excepting only that the design A/A* = 150,  instead of Figure 2’s 100.  Figure 2C below is the exact same thing yet again,  except that the design expansion ratio is A/A* = 200.   These were added to investigate the effects of higher expansion ratio upon the performance and dimensions of vacuum engines.

Figure 3 below is the same as Figure 3 in the original article above,  except that I corrected the error reporting max Pc,  and I added bell length.  This one is my “compromise design”,  in which I trade an over-expanded loss of Isp performance right at sea level,  for both higher vacuum Isp,  and a higher ascent-averaged Isp,  than a traditional sea level design.  It is a slightly-larger engine,  though.

Figure 4 below is the Table in the original article above,  enlarged,  and annotated for the important overall design considerations that impact vehicle design the most.  The basic data in the original table are unchanged,  just rows added representing the two vacuum designs with the larger expansion ratios.  Columns have been added on the right with values for A/A*,  exit diameter De,  and an estimate of bell length from throat to exit plane.   Annotations have been added as to what is most important for designing realistic vehicles.

Figure 1 – The Baseline Sea Level Design,  Perfectly-Expanded At Sea Level

Figure 2 – The Baseline Vacuum Design,  Unusable For Ascent,  Sized At A/A* = 100

Figure 2B – A Vacuum Design,  Unusable For Ascent,  Sized At A/A* = 150

Figure 2C – A Vacuum Design,  Unusable For Ascent,  Sized At A/A* = 200

Figure 3 – The “Compromise” Design,  Usable For Ascent,  At a Better Ascent-Averaged Isp 

Figure 4 – The Revised Comparison Table,  Annotated For Important Overall Design Considerations

The “compromise” engine is not quite as small as a true sea level design,  but it outperforms the sea level design for ascents overall,  and this would apply whether single or 2-stage.  

It is not as large as the three vacuum engines,  although it is fairly close in size to the A/A* = 100 design,  and in its vacuum performance. 

It is much smaller than the A/A* = 150 and = 200 designs,  and yet still does not fall all that far short,  in terms of vacuum performance (under 5% shortfall).  A factor of 1.050 on the velocity ratio dV/Vex is only a factor of about 1.051 applied between the corresponding mass ratios needed for vehicle or stage design.

The compromise design is like the other fixed-geometry designs:  it will have a very high engine thrust/weight ratio T/We ~ 50-100.  That cannot be true of anything that is variable geometry!

Conclusions

#1. If you are doing a 2-stage launch vehicle design (first stage expendable or reusable),  then use the “compromise design” approach to size your first stage engines.  They will outperform a conventional perfectly-expanded sea level design!  The downside is very limited throttle-down capability at sea level. 

Use a “vacuum design” at the largest dimensions you can tolerate,  for your expendable second stage engines,  since the stage point will always be essentially exoatmospheric,  and very near to horizontal flight. 

If your second stage is reusable,  it is unclear whether you need a mix of sea level and vacuum engines,  or you could just use engines designed with the “compromise design” approach.  The deciding factor will be the minimum thrust per engine to actually land. 

Vacuum designs cannot be used for this,  because they are always flow-separated near sea level.  The “compromise” approach may be separated,  if you have to throttle below its expansion design point.  Only the true sea level designs will be unseparated at both sea level and min throttle setting.

#2. If you are doing some sort of single-stage to orbit design,  use the “compromise design” approach in preference to the traditional perfectly-expanded sea level engine approach.  This will get you a higher ascent-averaged Isp than the traditional sea level designs can achieve. 

If this is to be a reusable design that lands vertically,  the problem is at landing,  when the weight is lowest.  It is launch that sets the summed thrust of all engines,  with due allowance for an engine or two nonfunctional.  At landing,  you need to be able to shut down enough of them so that the remaining engine or engines can be throttled down enough to land,  without suffering separation. 

What made the “compromise design” do better in ascent than a sea level design,  was sizing its expansion in the vicinity of 85% of max Pc.  That is a very small throttle range for vertical landing.  You may instead have to include some sea level engines for landing,  that can throttle deeply.

The way to avoid this issue is to land horizontally,  so that thrust at touchdown is not needed,  excepting perhaps a “go-around” capability.  The downside to this is far higher stage inert fraction,  inherent because of the required lifting shape,  whether winged,  or as a lifting body.  Exclusive of tankage and engine masses,  about the min credible airframe mass fraction will be near 10% or so.  The engines and the propellant tanks add directly to that!

#3. Why make this more difficult with heavier variable-geometry engines,  with a longer list of failure modes?  Why incur the low vacuum performance of free-expansion designs?  Neither option makes any practical sense.

------

Just in case you do not understand why free-expansion designs have lousy vacuum performance,  see Figure 5.  The nozzle kinetic energy efficiency reflects only the integrated average of the cosine factors for exiting streamlines that are not aligned with the thrust axis.  Such is measured after the last point of contact,  not before!   Thrust is measured just before the last point of contact,  not after!  This applies only to the momentum term m*Ve of thrust.  The as-expanded Pe*Ae term is usually smaller by far,  and does not get ratioed by the kinetic energy efficiency.

The usual nozzle average of cosine factors is literally the average of 1 on the centerline,  and whatever the outer-edge streamline cosine factor is.  That simple arithmetic average may not reflect the true integrated average.  However,  it is still somewhere in the ballpark!  And because of Prandtl-Meyer expansion effects at the outer edge of the exiting flow,  at high altitudes,  that edge cosine factor is very near-zero,  or even slightly negative!  Thus the nozzle kinetic energy efficiency is catastrophically low!  Almost no matter how you figure it!

And THAT is exactly why free-expansion nozzle designs of ANY kind,  are truly LOUSY vacuum engine designs!  They work better than conventional bells up to the lower stratosphere,  but they inherently degrade very quickly into uselessness,  much above the lower stratosphere. 

I know that many perceive it differently,  but you have been lied to,  for marketing purposes,  in a corporate welfare system.  Look instead at the actual engineering numbers.  And you will need to understand what Prandtl-Meyer expansion is,  in compressible flow,  to fully make sense of this. 

Figure 5 – Why Free-Expansion Nozzle Designs Always Have Lousy Vacuum Performance