Rough Correlation of Entry Ballistic Coefficient vs. Size for “Typical” Mars Landers

The Basic Problem

Larger vehicles tend to have higher ballistic coefficients for any given family of shapes. Hypersonic ballistic coefficient is mass divided by the product of blockage area and hypersonic drag coefficient (usually rather constant). The preferred metric units are kg for mass and square meters for blockage area. Drag coefficient is dimensionless, and depends primarily on shape in hypersonic flow. For blunt objects, hypersonic flow is Mach 3 and higher. For slender objects, hypersonic is Mach 5 and higher.

Unlike Earth, the thin atmosphere of Mars provides far less drag for braking during entry. All other parameters being equal, blunt entry vehicles of higher ballistic coefficient decelerate to about Mach 3 at lower altitudes. The experience at Mars (reference 1) has been that, for entry masses much over a metric ton, vehicles based on current technologies tend to come out of the hypersonics at altitudes too low for parachutes to provide much effective deceleration. This is compounded by terminal velocities on the chute(s) that are still supersonic. Thus, extensive final rocket braking is always required on Mars.

Any manned landings on Mars will require setting down 1-3 men (up to a ton), perhaps a couple of tons of supplies, maybe a ton or more of equipment, and around a ton for a rover “car” of some sort. This is just the “dead-head” payload. There are also the mass of the vehicle required to re-ascend to orbit, and the mass of the entry vehicle(s) that delivered all this stuff to the surface. Craft like that will weigh dozens to a few hundred tons at entry, depending upon propulsion type and vehicle layout. This is inevitable. These vehicles will have very large ballistic coefficients, and thus may actually strike the surface before the hypersonics end, at all but the very shallowest entry angles.

Landing on Mars with men is a very serious engineering problem, therefore. There are essentially only two ways around this dilemma, since even a simple minimal capsule carrying only 1 man plus landing propellant will weigh far more than a ton at entry. Those two are: (1) add extra blockage area at essentially the same mass (“inflatable heat shield”), and (2) add retro thrust during hypersonic entry to offset some of the mass, making the effective ballistic coefficient “appear lower”. One can also do both of these at once to get even more effect.

For any of these options, it is critical to understand the ballistic coefficient problem that we are trying to remedy. There is a need to estimate ballistic coefficient for very large vehicles quickly, so that “generic” studies may be performed early in the design process. Since most “back-of-the-envelope rocket equation studies” know masses better than dimensions, it is most convenient to correlate expected ballistic coefficient vs entry mass. I did exactly that herein.

Past Data

In reference 1 on page 4, table 1 contains data on every US Mars landing probe at sufficient precision to correlate ballistic coefficients. These include the two Viking landers, the Mars Pathfinder (MPF), the two MER landers (Spirit and Opportunity), and some pre-mission estimates for Phoenix and MSL (Curiosity) that are close enough for our purposes here. All of these share a 70-degree half-angle conical heat shield, with a rather squat aeroshell behind.

Here on Earth we have entry experience with ballistic warheads, the Space Shuttle, and 3 manned capsules that might resemble what we need: Mercury, Gemini, and Apollo. It is fairly easy to locate some dimensions for the heat shields for these on the internet. It is much harder to get mass at entry, especially for Gemini. Reference 2 had some very good dimensional data for Mercury, and reported a wide range of possible weights at entry that depended upon the mission duration. I used something closer to the long duration masses for purposes here. Reference 3 was unique, providing very good estimates of dimensions and masses for Gemini at entry, based on the post-entry example capsule in their passion. I got dimensions and masses for the Apollo command module from Reference 4.

The compilation of those data is given in Table 1, which is an image from a spreadsheet. Those data were in US customary units to better precision, so I converted them to metric for a better estimate of metric ballistic coefficient (beta) in the table. The Mars probe data were already metric, so I did not compute any US customary equivalents. For the old manned capsules, I obtained hypersonic drag coefficients from reference 5.

There are some differences here. The manned capsules have heat shields of a shape that is basically a spherical segment, and afterbodies of a rather tall form factor, leading to a rather large mass packed onto a smaller diameter. The exception is Apollo, which has a shorter conical shape, but is packed to a rather dense condition for its size. It was the largest and heaviest of any of the shapes. All of the Mars probes share a conical heat shield of 70 degree conical half-angle, with the point blunted. The afterbodies vary, but are all rather short for the diameters, leading to much lower masses packed onto any given diameter heat shield. I expected to see, and saw, rather scattered data.

Theoretical Grounds and Actual Correlations

All other proportions and form factors being equal, one would expect blockage area to vary with diameter squared, and volume to vary with diameter cubed. At a constant packing density, this means mass varies as diameter cubed. At constant form factor, drag coefficients would be equal. On this basis, one would expect that ballistic coefficient would correlate as proportional to diameter. That is not what happens, as is painfully evident in Figure 1.

The proportions and forms are anything but constant, and the packing densities vary even within the same form factors. Yet, bigger is both heavier and higher ballistic coefficient, generally. On that basis, there actually is a pretty good correlation of ballistic coefficient vs entry mass, which is only somewhat scattered. See Figure 2. I hoped that beta might correlate a little better as a power function of mass, and it did, as shown in Figure 3, which plots common log of metric beta vs common log of metric mass. That correlation curve fit equation is:

βpred, kg/m^2 = (374 kg/m^2)(entry mass, kg/5808 kg)^0.7752

The worth of this correlation is shown in Figures 1 and 2, where the correlation-predicted betas look pretty good vs mass in Figure 2, but are just as uncorrelated as the raw beta data vs diameter in Figure 1. The precision is poor, as are all log-log correlations. In this case, the raw data scatter about the correlation line by about a factor of 2 or 3, which is actually rather typical.

The exponent (slope on the log-log plot) corresponds to Apollo at the high end mass, and the smallest Mars probes at the low end. This may or may not overestimate the sensitivity of the beta to the entry mass, because the form factors are shorter for the probes. Yet, of the capsules, Apollo was the shortest form factor, not too unlike the probes. So my correlation may not really be that bad.

Using the Correlation

The results one gets depend upon the vehicle entry mass from whatever “back-of-the-envelope” model one is using for the Mars lander. The concept used in references 6 and 7 was a one-stage, reusable, 60 metric ton nuclear vehicle. At 60,000 kg, that vehicle would calculate as a ballistic coefficient of about 2286 kg/m^2 by the correlation. The old manned space capsules ranged from 246 to 374 kg/m^2. The Mars lander probes ranged from 64 to 115 kg/m^2.

Assuming a spherical heat shield shape, and a form factor like the Apollo, one would use an Apollo-like drag coefficient of 1.30, and calculate a diameter near 5.1 m for the 60-ton lander. Apollo calculates at an external-volume “packing density” of about 373 kg/m^3. Using the Apollo packing density, we would calculate a lander external-volume near 160 m^3. A conical shape of that volume is around 23 m tall at 5.1 m diameter, which is a much slimmer and taller form factor than Apollo. Drag coefficient for a shape like that is closer to Mercury’s 1.55 than Apollo’s 1.30, so we must iterate.

Actually, landing stability considerations on rugged ground demand that the height be much closer to the diameter. At the Apollo packing density, that 60 tons would correspond to the same 160 m^3, but at a diameter equal to the height at about 8.3 m. Using the Apollo drag coefficient, the beta calculates as 853 kg/m^2, which is factor 2.7 lower than the correlation would predict for that mass. That is within the scatter inherent in the correlation, so it is still “reasonable”.

The upshot of all this is that a reasonable exploratory beta for entry calculations might be in the neighborhood of 1000-1500 kg/m^2, for a lander in the 60 ton entry mass range. That’s good enough to get started, working on entry, deceleration, and touchdown issues. That particular mass was intended for modeling a reusable single-stage nuclear vehicle. Staged chemical designs would be in a different, larger class of entry mass. However, the same landing stability considerations apply, one way or another.

References

1. R. D. Braun and R. M. Manning, “Mars Exploration Entry, Descent, and Landing Challenges”, meeting paper downloaded from the internet, undated except no references newer than 2006.

2. Encyclopedia Astronautica article found on the internet via search keyword “Mercury capsule”, including dimensional and mass data, and a very good chronology of the entire Project Mercury effort.

3. Smithsonian exhibit article found on the internet via search keyword “Gemini capsule”, describing a recovered example of an actual Gemini capsule, in what is very close to the entry mass configuration. This is quite different from other articles, which include the retro and on-orbit service modules in their dimensions and masses, more in line with the configuration at separation from its booster.

4. Wikipedia article on the Apollo command and service modules, found via search keyword “Apollo capsule”. The data on the command module alone is very close to the entry configuration.

5. Sighard F. Hoerner, “Fluid Dynamic Drag”, section 18, figures 44 and 45. Published by the author, 1965.

6. G. W. Johnson, “Going to Mars (or anywhere else nearby) the posting version”, based on a paper given at the 14th annual Mars Society convention, in Dallas, Texas, August 2011. See the article dated 7-25-11 on http://exrocketman.blogspot.com.

7. G. W. Johnson, “Mars Mission Second Thoughts Illustrated”, a follow-up article to the convention paper in reference 6, see the article dated 9-6-11 on http://exrocketman.blogspot.com.

Table 1 – Spreadsheet Database of Dimensions, Entry Masses, and Ballistic Coefficients



Figure 1 – Ballistic Coefficient vs Diameter Does Not Correlate


Figure 2 – Ballistic Coefficient vs Entry Mass Correlates Loosely


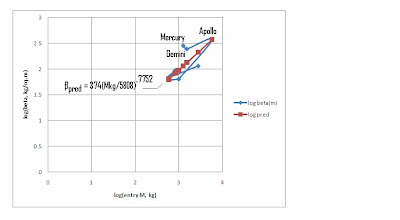
Figure 3 – Log-Log Plot of Ballistic Coefficient vs Entry Mass (Common Log Basis)


An Update: Further Analysis and Refinement (8-2-12)

The data trend through the Mars landers and the Apollo capsule under-predicts beta for the Mercury and Gemini Capsules, and so may well over-predict beta for very large objects. Accordingly, I tried a fit through just the capsule data, and fitted to the Apollo data, with an exponent of 0.2083. This trend way over-predicts beta for the landers, and so may well under-predict the beta for large vehicles. The equation and trend line are shown in Figure 3B.


Figure 3B – Modification of Figure 3 with Capsule Data Only Trend

Something intermediate was needed, so I averaged the two exponents to 0.49, and fitted it to the Apollo data as beta, kg,sq.m = 374*((M, kg)/5808)^0.49. This trend “splits the difference” fairly well between the lander probe data and the manned capsule data. All three are shown in Figure 4 for the range of masses covering the landers and the capsules. Figure 5 shows the same three trends extrapolated to very large vehicle masses, up to 300 metric tons. Of the three trends, the intermediate trend seems the most “reasonable”, but this is just a guess on my part.

In the absence of any better information, I would now scale beta vs mass using the intermediate trend equation given just above, at exponent 0.49, fitted through Apollo at 5808 kg and 374 kg/sq.m.


Figure 4 – Comparison of the Prediction Trends with Data


Figure 5 – Extrapolations with the Trends to Very Large Masses

Rough-Out Mars Mission with Artificial Gravity

Purpose

The purpose of this particular study was to show how easy it is to supply artificial gravity to the crew of any reasonable candidate design for a manned Mars mission. No gigantic “Battlestar Galactica” or complicated Rube Goldberg cable-connected designs are necessary.

All you need is a radius exceeding 56 m from the center of gravity of a long, slender orbit transport to the habitat at one end. The gee level achievable this way is 1 full gee at 56 m for a “fuzzy” maximum rotation rate speed limit of 4 rpm. Longer radii allow lower, even more tolerable, rotation speeds.

Mission Architecture and Vehicles

The mission plan outlined here uses two vehicles sent by Hohmann transfer from low Earth orbit (LEO) to low Mars orbit (LMO). One is the manned vehicle, spun for artificial gravity, the other is an unmanned transfer of the return propellant supply for the manned ship. Both are propelled by solid-core nuclear thermal rockets, using liquid hydrogen propellant.

Two mass allowances for otherwise-undefined landers are included in the manned ship. The landers, empty tanks, and one supply storage module (loaded with wastes) are left in LMO. The manned ship is much smaller in mass for the return to LEO, but still about the same overall length. Modular vehicle design is what allows this mission architecture (a key point with this design study).

Why Do It This Way Instead of Direct?

There are two excellent features of plans like this: (1) staging from LMO allows more than one landing to be made during the one trip, and (2) returning much of the manned vehicle to LEO allows re-use of major components for other missions, components that do not need to be launched again, only re-supplied. Both of these dramatically increase the usable results obtainable from the one mission.

This particular mission design also has two serious downsides. One is that if rendezvous fails in LMO, the crew dies. Their return propellant supply must be rendezvoused-with in LMO, there is no other option. I would not seriously propose this particular plan for actual implementation, precisely because of that lack of “a way out”, even though that event is very likely low-probability.

However, this mission design study is a “representative plan” for illustrating the incorporation of the artificial gravity that we already know the crew will need.

The other downside is lack of a crew return vehicle to be used for emergency free return, should the final return-to-LEO burn fail. Being a multi-engine propulsion module, that event is also low probability, but there is no other option for reaching LEO or Earth. If that event should occur, again the crew is lost. So, for that reason as well, I would not propose this particular architecture as a serious plan. Again, it merely provides representative vehicles for examining the artificial gravity issue.

There is one other mild “downside” to this particular architecture: there must be propulsion on the landers, but also on the unmanned supply vehicle. There would be fewer” dead-head” tons to ship, if the lander propulsion could also be used to push part of the propellant supply to Mars. However, the design criteria for lander propulsion could well be incompatible with the propulsion needs for transit from LEO to LMO. With an undefined lander design, that option could not be utilized in this study.

Velocity Requirements

These were assumed to be the same as from my earlier studies (reference 1): 8 km/sec one-way, orbit-to-orbit, LEO to LMO, and the same again to return. This requirement would include escape and capture burns at average planetary orbital parameters, with crude allowances for plane changes, and for propellant boil-off losses. These are representative, and a bit conservative, and so are not “accurate” for any given scenario.

Crew Habitat Modules

My design requirements for habitat open space per person, and consumables per person, were just “good guesses”. I tend to use larger volumes of free space per person than other designers. This is based on my own living room’s volume at home, and the perception that I could not share that volume with more than one other person for around 2-3 years of forced confinement. Prisoners in most state prisons share smaller spaces, but psychologically, they would not make very good astronauts, even if they were not criminals. Some designers might find my habitats overly-spacious, but I don’t think they are. This is a “fuzzy choice” that must be made, that seriously impacts the sized of vehicle designs.

See Figure 1 below for the two-module habitat I came up with. By my criteria, this is big enough for a crew of 6, and would contain a large common room, exercise facilities, sleeping cubicles, the flight control station, “ from-orbit” science stations, and a galley area. The water and wastewater tanks should be arranged around the flight control station, so that it can also serve as the temporary solar flare radiation shelter for the entire crew. The dimensions and masses of the modules as I estimated them are compatible with single launch by Atlas-V-552, or both-at-once by Falcon-Heavy.

Engine Module

I assumed data from the final tests of the old “NERVA” nuclear engine from 1972-1973, just as Project Rover shut down. This was the engine that was essentially flight-qualified, but never actually got to fly. There are better designs, but none of those got the testing required to be flight qualified. Data are shown for a multi-engine module in Figure 2 below, to take advantage of multi-engine reliability. This could be 2, 3, 4, or even 5 engines. Module sizing requires at least 0.05 gees vehicle acceleration in order to be impulsive enough not to suffer the velocity losses of long-burn / low-thrust schemes.

This module sized-out at not quite 12 metric tons. That would be compatible with an Atlas-V launcher, or a Falcon-9 (by Spacex’s 2012 website data), if dimensions can be resolved for a practical partial shroud size. Otherwise, the individual engines and components could be launched separately and assembled in LEO. Two of these modules are necessary: one for the manned vehicle, the other for the unmanned vehicle.

The spreadsheet inputs for velocity requirements, engine module, and habitat modules, are imaged in Figure 3 below. User inputs are highlighted yellow. User interventions-to-converge are blue.

Storage Supply Modules

The basic masses and dimensions of the two storage supply modules are given in Figure 4 below. These two can support a 27-month round trip with consumables masses that seem realistic, even by some of the online mission resource calculators that now exist (see reference 2). The packaging density is far higher than the habitat modules, as there is almost no free volume inside. This affects their shape.

The excess consumables mass that I used (relative to the online calculator results) should “cover” the use of bulky, heavy frozen food supplies. These are required for a 27 month round trip, since the conventional non-frozen dehydrated or sealed astronaut foods cannot last the mission time without decomposing. Those are typically “gone” after about a year to 18 months.

Propellant Modules

Storage of liquid hydrogen over 2-3 year timelines is an engineering issue that is still unresolved, although it could be resolved very quickly. I am assuming these propellant tank models include a dewar-as-inner-tank, external insulation that includes foam/foil layered meteoroid armor, a deployable sunshade, and deployable solar power wings to power cryo-cooler equipment. Accordingly, the volumetric load-out factor is lower, and the inert weight factor higher, than most folks in the spacecraft business would assume. These are “good guesses” only, to cover the extra equipment.

The mass and dimensional data are given in Figure 5 below. It is presumed that one simply stacks up enough of these modules to achieve the velocity requirement. Uniquely, that stack of modules may be multiple linear arrangements tied together in parallel, in order to achieve the necessary form factor without being excessively long or short. The modules are deliberately sized to launch one at a time on an Atlas-V-552 configuration, or two-at-once on a Falcon-Heavy.

The inputs to the spreadsheet regarding the storage supply modules and the propellant tank models are imaged in Figure 6 below. User inputs are highlighted yellow. User interventions-to-converge are blue.

Manned Transport, Outbound Configuration (to Mars)

Sizing this vehicle to an acceleration requirement set the mass of the engine module and the total engine thrust. This was an iterative process. The as-sized vehicle is in the 840 metric ton class, at ignition departing from LEO. It departs at 0.05 gees initially, which is impulsive enough to avoid low-thrust losses. It is depicted in Figure 7 below.

This vehicle includes two undefined Mars landers, in order to make two separate landings at different sites during the one mission trip. These are included as mass allowances only, depicted schematically in Figure 8 below. Each lander is 60 metric tons, assembled from two items docked in LEO that are in the 30-ton class. These components probably require Falcon-Heavy launchers.

Figure 9 below is a spreadsheet image that gives the as-sized details of masses and module count for the manned transport in this outbound configuration. There are a total of 23 propellant tank modules, arranged as a triple stack 7 units long plus a double stack one unit long. The habitat and storage modules are a linear string at one end, with the engine module at the other.

Vehicle center of mass is near the middle of the overall length. The radius from there to the middle of the habitat is long enough to provide one full gee artificial gravity at about 3 rpm, spun “head-over-heels”. This is a rigid slender baton, not too slender to be structurally sound. This is stable dynamically, and easy to de-spin for maneuvers, and re-spin afterwards.

This demonstrates just how easy it is to incorporate one-full-gee artificial gravity into a design not otherwise overtly driven by artificial gravity concerns. It just can naturally happen. No giant structures, no space trusses, no spinning crosses, no cable-connected modules. Just a rigid slender baton-like structure spinning end-over-end. Spin-up and de-spin are just thruster firings, anytime needed.

Manned Vehicle Return Configuration (to LEO)

For the return, half the supplies are already consumed, so one storage module can be left at Mars in LMO, containing wastes not otherwise disposed-of. The landers are left in LMO, as is the entire outbound propellant tank cluster, now empty. The two habitat modules, one storage module, the return propellant tank stack of 9 modules, and a NERVA module comprise the return vehicle configuration, depicted in Figure 10 below. (The other NERVA module and a cluster of empty tanks from the unmanned vehicle also remains in LMO.) The spreadsheet data corresponding to this configuration are imaged in Figure 11 below. Note that the NERVA engine module, operated at the same design thrust as outbound, now provides 0.13 gee acceleration at ignition in LMO.

This configuration is a simple linear stack, no parallel clustering. It is far less massive (330 ton class), but about the same overall length as the manned outbound vehicle, and also just about the same radius from center-of-mass to middle of the habitat. Again, one full gee of artificial gravity is available at about a 3 rpm spin rate, “head-over-heels”. This demonstrates again just how easy it is to incorporate one gee artificial gravity into a representative very-practical design, without driving that design to extremes by the artificial gravity requirement. The modular approach provides the form-factor tailorability that is absolutely necessary to achieve this result.

Unmanned One-Way Propellant Supply Vehicle

The return from Mars depends upon 9 propellant modules sent there separately. Those modules, plus a small guidance and control unit, plus another of the same NERVA engine modules plus a propellant tank cluster for the trip, comprise the one-way propellant supply vehicle. Being unmanned, this vehicle does not spin for artificial gravity. It is depicted in Figure 12 below. The as-sized mass and module numbers are in the spreadsheet image of Figure 13 below.

There are 9 propellant modules that are the payload. It takes another 19 such modules to send this payload from LEO to LMO, again with the same NERVA module at the same design thrust. That vehicle is arranged as a 10-module center stick, surrounded by three 6-module sticks spaced equally circumferentially. The result is a vehicle about 160 m long, in the 700 ton class at ignition in LEO. Initial acceleration is 0.06 gees. Other stack configurations are possible, of course.

Launcher Count and ROM Program Costs

Figure 14 below provides an image from the spreadsheet of the module count and two options for the corresponding launch rocket requirements. Launches for transferring the crew to and from the vehicle in LEO are included (either as something 6-man-caopable on an Atlas-V, or as a Falcon-9/Dragon).

The two options maximize either United Launch Alliance (ULA) launcher usage or Spacex launcher usage. See reference 3 for data regarding launch prices. The “truth” lies in a mix of launchers in between these extremes, so that the ultimate rough-order-of-magnitude (ROM) program costs reported here are the average of the two numbers computed for the two options. Launch costs were arbitrarily assumed to be 20% of total program outlays. That would be realistic for a program managed by a lean focused agency, and conducted by lean, focused contractors, with little or no new technology development, only implementation-design efforts.

Not only are the ROM estimates of total program cost in the figure informative, but also the costs per landing site visited, and per person sent. These are good “bang-for-the-buck” measures. Any way one looks at these numbers, they are startlingly lower than the preconceptions or preferred beliefs of most folks. They are radically lower than most of the Mars mission proposals coming from NASA in the last couple of decades. This is a remarkable result, considering that this is not a “minimalist” mission design. We are looking at two vehicles in the 800-900 metric ton class, as assembled in LEO. We are looking at sending a crew of 6 to Mars here.

Conclusions

The mission architecture and vehicle designs of this study are not the architecture and designs that should actually fly. But, they are similar enough to what should really fly, that the issue of artificial gravity can be realistically investigated.

Very important: It is the modular spacecraft design approach that allowed tailoring vehicle form-factor at any given mass to obtain a convenient radius length, for easily designing-in artificial gravity at 1 full gee, by simple end-over-end spin of a “slender baton”.

Using a mix of ULA and Spacex launchers, direct launch costs are estimated somewhere near $6.4 B, based on current retail launch prices.

Overall program outlays were ROM-estimated from the assumption that launch costs are around 20% of total program outlay. Thus the entire mission cost is near $32 B, which is far lower than the $400-500 B numbers that Congress saw from NASA recently.

“Bang-for-the-buck”: program ROM costs are near $16 B per site visited, and near $5.8B per man sent to Mars. That last is about the same as those claimed for the minimalist mission designs, but the return here is far larger (in terms of sites visited and persons sent). More sites and bigger crews always mean that more and better information can be obtained and brought home.

It is the LMO basing that allows multiple landings, which in turn produces more return for the cost. Therefore, this should be the preferred architecture for exploration-type missions. (Establishing bases or experimental stations on the surface is a different type of mission entirely, although an exploration mission can also do some of those things.)

There is a mission architecture and vehicle design opportunity that I could not take advantage of in this study, with its undefined lander. That would be to use the lander propulsion as the transfer propulsion for sending some assets to Mars. That would be more like the designs outlined in reference 1.

This Study Achieved Its Overall Purpose vs the Artificial Gravity Issue

Achieving 1 full gee of artificial gravity need not drive vehicle designs into gigantic, complicated or unrealistic forms, nor need it drive launch and program costs up. The key is form-factor adjustment for a given mass, as enabled by modular vehicle design. The preferred form-factor is the “slender baton”, for end-over-end spin at low, tolerable rates (under about 4 rpm maximum).

References

1. Updated version of paper presented at 14th Mars Society convention in Dallas, August 2011. See http://exrocketman.blogspot.com, article dated 9-6-11, titled “Mars Mission Second Thoughts, Illustrated”.

2. On-line supplies calculator application: see http://www.5596.org/cgi-bin/mission

3. Launch cost data plots posted in: http://exrocketman.blogspot.com, article dated 5-26-12, titled “Revised, Expanded Launch Cost Data”.



Figure 1 – Crew Habitat Module, One of Two Total for a Crew of 6


Figure 2 – Multi-NERVA Engine Module, and the Guidance and Control Package


Figure 3 – Spreadsheet Inputs for Velocity Requirements, Engine Module, and Habitat Module


Figure 4 – Storage Supply Module, One of Two Required


Figure 5 – Data for Common Propellant Module


Figure 6 – Spreadsheet Inputs Image for Storage and Propellant Tank Modules


Figure 7 – Manned Transport in Outbound Configuration (to Mars)


Figure 8 – “Dummy” Mass Allowances for Undefined Mars Lander Vehicle, 2 Required


Figure 9 – Spreadsheet Image for As-Sized Manned Transport, Outbound Configuration


Figure 10 – Manned Transport in Return-to-LEO Configuration


Figure 11 – Spreadsheet Results for Manned Transport, Return-to-LEO Configuration


Figure 12 – Unmanned One-Way Return-Propellant Delivery Vehicle


Figure 13 – Image of Spreadsheet Data for Unmanned Return-Propellant Vehicle


Figure 14 – Launcher Counts and Costs, and ROM Program Costs

Gravity Data on All the Interesting Worlds

I used the 53rd edition of the CRC Handbook of Chemistry and Physics to compile this data set, because it is in my physical library. This reference dates to its copyright date of 1972. There may exist better data of more recent origin, but this is “pretty good” stuff, as of 1972. See section F of said reference, pages F150-F161.

I looked at the nearby planets of interest for manned landings: Mercury, Earth (as a reference), and Mars. I also looked at the other objects of interest to manned landings anytime in the foreseeable future: our moon, the four Galilean satellites of Jupiter (Io, Ganymede, Callisto, and Europa), Titan around Saturn, and the four largest asteroids. The more distant gas giants are not so much of immediate interest for manned landings. The asteroid data were rather speculative in 1972.

I used the reference cited above to compile planetary mass and radius data, from which I computed surface gravity and surface escape speeds. These I compared to the tabulated “standard” values, which correlated to about 4 significant figures (see figure 1). This includes the centrifugal force effect at 45 degrees latitude, as best it was known in 1972.

Therefore, as best we knew the mass, radius, and rotation rate data in 1972, these values of surface escape speed and surface circular orbit velocity reported herein, are “good”. See figure 1 for an image of the spreadsheet data. Use the “standard” values in preference to my “calculated” values. More significant digits are implied in those “standard” values. The digits for the universal gravity constant don’t all show in the spreadsheet cell, but they are all there: 6.6732 x 10^-11 N m^2/kg^2, per the cited reference.

UPDATE 2-20-17:  The listed "standard" escape speed (and associated circular orbit speed) data in the old CRC handbook are just wrong for Ganymede and Titan.  Use my calculated values instead.  Edited spreadsheet image also revised to call out incorrect data.  

You may scale surface values of escape speed and circular orbit speed to “realistic” altitudes by means of body radius, as given below:

V at altitude z, km/sec = V at surface (km/sec) * ((R body, km)/(R body + altitude, km)^0.5

I have yet to work out what “realistic” factors might apply. But, the circular orbit speed at altitude is a good zero-order estimate of the theoretical delta-vee required to reach orbit from that surface. This needs to be factored up by gravity losses of about 1.05 on Earth, and by drag losses of about 1.05 on Earth, for the typical slender, relatively low-drag, vertical launch vehicle. There are also out-of-plane orbit issues to consider.

Figure 1 – Image of Spreadsheet Data  (UPDATED 2-20-17)

“Back of the Envelope” Entry Model

In a previous article, realistic atmosphere models were determined, and extended to include speed-of-sound profiles (see “Atmosphere Models for Earth, Mars, and Titan”, dated 6-30-12). These were based on atmosphere data reported by Justus and Braun (reference 1). Those Justus and Braun atmosphere models included recommendations for a density scale height model, also reported in the 6-30-12 article. This would be used for simplified entry dynamics and heating calculations, the topic here.

Update 1-21-13:  Please see the newer posting,  dated 1-21-13 and titled BOE Entry Model User's Guide,  for more details on how to set up and use this spreadsheet model.  

Update 3-23-13:  I have since found that the simplified entry model described in the Justus and Braun paper actually refers to the early 1950's work of H. Julian Allen at NACA.  He was able to publish this model openly in the mid-1960's,  after it was declassified.

Density-Scale Height Model

As reported in reference 1, for regions where the density scale height is relatively constant, there is a simple exponential correlation of density versus altitude. The density scale height is defined as density divided by its own gradient (with altitude):

Hρ = ρ / (dρ/dz) where z is altitude

In regions where this scale height is at least approximately constant, the relationship between altitude and density is well-approximated by a two-parameter fit:

ρ(z) = ρ(0)*exp(-z/Hρ) where “exp” is the base e exponential function

In this equation, ρ(0) is a curve fit parameter only, and may not correspond to surface density at all. The values of ρ(0) and Hρ applicable to entry altitudes for Earth, Mars, and Titan were reported previously in the 6-30-12 article, exactly as given in reference 1.

Vehicle Model

In hypersonic flow, the drag coefficient of an object is essentially a constant across a broad range of flight Mach numbers, from entry speeds down to a “low limit”. That low limit is roughly Mach 3 for a blunt object, and about Mach 5 for “sharp” or “pointy” objects. Most capsules entering blunt-heat-shield-surface-first are “blunt” objects, with a lower Mach limit of about 3, for applicability of any and all hypersonic flow models.

In most models, the parameter of interest is the ballistic coefficient β, which is computed from the vehicle mass m, blockage area A, and hypersonic drag coefficient CD, as below. The usual units these days are kg for mass and square meters for blockage area. CD is nondimensional.

β = m / CD*A

The values of β tend to be smaller numbers at smaller masses, and larger at higher masses. That scaling with vehicle mass is a topic for another article. The largest value in reference 1’s study was β = 200 kg/sq.m, and that is the value used here. It is larger than that for all probes sent to Mars so far.

The larger the β, the deeper into the atmosphere the body penetrates during the hypersonics. This also acts to raise maximum gees and the heating experienced during the entry.

Entry Model

There are three important parameters, all associated with the location of the “atmospheric interface”, where deceleration effects due to drag begin. This is a “fuzzy” notion, so the choice is a bit arbitrary. It is usually based on a density value. The geometric altitude at interface zatm, varies from one celestial body to another. The velocity at interface Vatm can vary widely, from above escape Vesc to below circular orbit velocity, depending upon circumstances. Vesc itself should be adjusted from the surface value to the interface altitude:

Vesc at zatm = surface Vesc * (R / (R + zatm))^0.5 where R is the body’s radius

The circular orbit velocity is very simply related to the escape velocity. For entry analyses, this should be done at zatm. After a de-orbit burn, the actual entry velocity will be very little different from the circular orbit velocity.

Vcirc at zatm = Vesc at zatm / (2)^0.5

For vehicles coming in from deep space for a faster-than-escape entry, there is a velocity V∞ typical of its interplanetary orbit, in the absence of the influence of the local body’s gravity. As the vehicle approaches the body, its gravity affects vehicle relative velocity at interface. This effect can be computed from kinetic energies:

Vatm = (V∞^2 + Vesc^2)^0.5 where Vesc is the value at zatm

There is also an entry angle θ from local horizontal. This is best visualized in “flat Earth” Cartesian coordinates. The simplified entry model presumes the trajectory to be a straight line for non-lifting vehicles, and that really is a realistic notion for the hypersonics. From the change in altitude and the tangent of θ, the horizontal change in range is calculated. Using instead the sine, one may compute the change in slant range down the trajectory line. These increments can be summed up. See also figure 1 below. The “end” of this analysis would be when velocity drops to about local Mach 3, computed as velocity divided by sound speed at that altitude. (That does not have to be very precise.)

The steeper the θ (angle below horizontal), the deeper into the atmosphere the vehicle penetrates during entry. This acts to raise deceleration gees and heating, plus the altitude at end-of-hypersonics is lower.

Here are the entry interface altitudes recommended in reference 1:

zatm, km body
140 Earth
135 Mars
800 Titan

The entry velocities I used in my study here are just escape speeds at interface altitude, typical of a V∞ = 0 situation for Earth and Mars. The escape speed on Titan is not even hypersonic, so I chose an utterly arbitrary value, just to have some numbers to analyze. The surface escape speeds are also given, so you can see the effect of scaling to zatm for Earth and Mars. These values are:

Vatm, km/sec body surface Vesc, km/sec
11.058 Earth 11.179
5.026 Mars 5.0282
3 (arbitrary) Titan 0.8161   UPDATE 2-20-17 should be 2.58 km/s

Velocity Trend from Simplified Model


Velocity down the trajectory is related to the scale height and vehicle parameters by:

V(z) = Vatm * exp(-C * exp(-z/Hρ)) where z and Hρ are km, and the velocities are km/sec
C = (ρ(0) * Hρ * 1000)/(2*β*sinθ) where Hρ is km, ρ(0) is kg/cu.m, and β is kg/sq.m

In my version, θ is positive downward, requiring the negative sign on C in the argument of the exponential in the V equation. This is different from the positive upward convention in reference 1, where the sign on C was positive, because its value was already negative, due to the sign on the sine. Reference 1 was “hazy” on units of measure, but those are clarified here. The “1000” in the C equation given here converts scale height units from km to meters, so that C may be dimensionless. Reference 1 does not show that.

Repetitive calculations across a spread of altitudes (from zatm downward) produce a list of V values, one for each z. The corresponding horizontal and slant ranges may be computed from zatm and θ as below. This leads to a list of velocities versus slant ranges that may be plotted. This is the velocity profile down the slant line trajectory, something not presented in reference 1, but actually quite useful.

R(z), km = (zatm – z, km)/tanθ
S(z), km = (zatm – z, km)/sinθ

From one point to the next going downward through the list vs altitude, velocities may be averaged, and the slant range distances may be differenced. Slant range distance increment divided by average velocity in that increment is the time increment from the one point to the next in the list. These may be summed from 0 at interface to produce a timeline down the trajectory. If the list of altitudes is fine enough, these timeline calculations can be rather accurate. Because altitudes are km and velocities are km/sec, times in this timeline will be seconds. Entry can be hundreds to thousands of seconds long (a few to several minutes).

A profile of deceleration gees may be computed using that timeline. From one point to the next, the difference in velocities divided by the difference in times is the acceleration in absolute units. Times will be seconds, but velocities must be in m/sec, requiring 1000*km/sec values. If you do this, accelerations will be in m/sec2. Divided by the standard value 9.8066 m/sec2, this is deceleration gees. This produces a list of gees vs. slant range as a deceleration profile down the trajectory. It invariably shows a peaked behavior. The peak value value computed this way compares very closely with the closed-form max gee equation used in Reference 1. The old model also includes closed-form equations for the velocity and altitude at which gmax occurs. These correlate well with my numerically-accumulated solution, leading to the conclusion that Justus and Braun modeled the deceleration dynamics rather well in their paper.

Convective Heating Model

There actually are some useful simple models for stagnation point convective heating during entry. Radiation heating is not so simple, but does range from a significant to a dominant effect. The incandescent dissociated gas adjacent to the spacecraft is, quite simply, a very bright, hot fire warming the surface. In the absence of any calculations at all, a rough-and-ready rule of thumb might be to triple the convective values. However, that is not a proper basis for actual design. Neither are convective values alone. “Fixing” this is beyond scope in this article.

Reference 1 used one of the simplest of the old convection correlations. It relates stagnation point heat flux to nose radius rn, ambient density ρ, and velocity V. This is a dimensionally-inconsistent correlation equation with a constant of proportionality k that includes the conversion of the units of measure. I found very serious problems with the use of this equation in the heating analysis of reference 1. One problem was the identification of this constant of proportionality k as a “heat transfer coefficient”, which it most definitely is not. Here is the correlation equation:

q = k (ρ/rn)^0.5 V^3

I found in a much older reference (2) this same correlation set up for American units of measure. Nose radius was feet, velocity feet/sec, density lbm/cu.ft, and heat flux BTU/sq.ft-sec. For these units, k was numerically 3.16 x 10-9. Carefully converted to metric units (nose radius m, velocity m/sec, density kg/cu.m, and heat flux W/sq.cm), k should numerically be 1.748 x 10-8. That is not what I found back-calculated from the heating data reported in reference 1. They were using 1.006 x 10-8 for the peak heat flux model, and 1.575 x 10-15 for the total heat absorbed model. Those differ by 7 orders of magnitude, not the 3 orders of magnitude that account for the change from W-sec = J to KJ units.

The old analysis reported in reference 1 did not compute heating down the trajectory, only the closed-form equations for peak heating and the velocity and altitude at which it occurs, plus a closed-form equation for total heat absorbed during entry (representing the time integral of the heating rate). The equations presented for this in reference 1 show the same variables k, rn, plus ρ(0), Hρ, and Vatm. It’s supposed to be the same k, but it is not the same k in reference 1.

For the units they used, the two k-values should have differed only by the factor of 1000 to convert J to KJ units. Both were per sq.cm, and per sec of time in the flux. Reference 1’s actual k numbers differed in the significant digits between flux and total heat, plus 4 extra orders of magnitude in the power of 10. The one used for heat flux differed from the correct value by about a factor of 1.5, which is not all that significant, although their error is in the under-prediction (wrong) direction. They also used different values at Mars from those at Earth. These numbers strongly resemble arbitrary selections to match a known heating point to the corresponding variable values in the equation, not consistent use of the correlation.

I did not do any of that. I used the correct metric k-value in the heat flux correlation, directly in my developed numerical trajectory list, producing a heat flux value at each point analyzed. My heating peak value differs from reference 1’s closed-form estimate by the ratio of the k-values used. My altitude and velocity at peak heating resemble those of reference 1. That part of the reference 1 heating estimates is good to the factor 1.5 difference in k-values that we used.

I numerically integrated my heat flux values with time, using the timeline developed in the list. My integrated total heat does not match the closed-form estimate at all (I did that, too). The significant digits are close, but my closed-form data show a 7-orders-of-magnitude problem with the powers of 10. I cannot find the error in the closed form equation for total heat, but it is there. The integrated total does look reliable, though, in my trajectory listing. I suspect that this discrepancy in the answers from the closed-form equations versus integrated totals is why no one used this old model for any heating estimates. Corrected like this by numerical integration, it now looks good to me. Do not use the closed form heating estimates, use the trajectory listing and integrated total instead. This is easy to do in a spreadsheet.

The Trajectory Selection Process

I did not iterate to optimize entry trajectory in any way for this article. For a true design study, one would follow the sequence in figure 2 below to determine the Mach 3 “end-of-hypersonics” slant range and velocity from the velocity vs. slant range plot. Those endpoint conditions can be transferred to the other charts, which determines “end-of-hypersonics” altitude, from the altitude vs. range plot. The peak gees can be read from the deceleration gees vs slant range chart. Peak convective heating rate and total convective heat absorbed can be read from the heating vs. slant range chart. The iteration is on peak gees and altitude at end-of-hypersonics, which have practical limits (max gee, min altitude). The heating parameters just feed into a thermal protection system (TPS) design process. The variables you change to optimize your trajectory selection are θ, β, and perhaps the selection of Vatm.

Calculated Data for Unoptimized Trajectories

I ran escape-speed models for Earth and Mars, at 1 degree below horizontal and β = 200 kg/sq.m. These compare directly to the 1 degree, β = 200, V-at-infinity= 0 cases in reference 1. For Titan, my arbitrary Vatm was 3 km/sec, so those data do not compare to anything in reference 1.

The sequence of figures for Earth entry is figures 3, 4, 5, and 6 below. These are presented in analysis sequence order. Figure 3 is the velocity profile vs slant range plot. Using the speed-of-sound profile for Earth’s atmosphere, one can select which point in the tabulated list is closest to Mach 3. (Mach number is velocity divided by sound speed, same units for both.) Sound speeds in that part of the atmosphere are around 300 m/s, so 1 km/sec is pretty close to Mach 3. The spreadsheet list (imaged in figure 7) tells us which altitude is the end-of-hypersonics altitude. That point is then marked in the figure. We also have the end-of-hypersonics slant range from the list.

The second plot is range and slant range vs altitude. At only 1 degree depression, these two happen to fall just about on top of each other in the figure. The Mach 3 point can be marked using the altitude from the list, as selected from the previous figure.

The third plot is the deceleration gees vs slant range profile. End of hypersonics can be marked with the slant range determined from the Mach 3 point above. The peak deceleration gee can be located on the graph, and picked out of the list, including its corresponding altitude and velocity.

The fourth plot presents the heat flux and integrated total heat vs slant range profiles. End of hypersonics can be marked with the slant range determined from the Mach 3 point above. The peak convective stagnation point heat flux can be located on the graph, and picked out of the list, including its corresponding altitude and velocity. The integrated total at the end-of-hypersonics is the value at the end-of-hypersonics point (the Mach 3 point).

For Earth, I could enter steeper and still stay below the 11 gees we used in Apollo returning from the moon. This shouldn’t be a problem for too low an end-of-hypersonics altitude, as that was over 40 km for 1 degree. This study has not yet been run by me, but would produce different outcomes for each β and Vatm selection. Having a “map” of these variations quickly was the advantage of the way this type of analysis was done in reference 1. For the dynamics, reference 1 provides good data; just not on the heat transfer.

The same sequence of plots for Mars is given in figures 8, 9, 10, and 11 below. Results look similar, except that gees and heating are much lower. So also is altitude at end-of-hypersonics. For Mars, I could enter steeper at higher gee, but this would put the end-of-hypersonics altitude even lower, and it is already fairly low. Higher β just makes this quandary even worse. That is the basic problem with traditional entry and supersonic/subsonic deceleration on Mars: little or no solution space adequate for effective chute-assisted descent. That spreadsheet is imaged in figure 12.

Even lift during the entry hypersonics won’t help that picture very much. Reference 3 discusses some ways and means around this quandary. Personally, I favor using lift and retro thrust through entry, and thrust all the way to touchdown; probably low thrust during the entry, and low thrust with the chute (if any), then high thrust to touchdown. Thrust offsets some of the mass’s inertia during deceleration, effectively lowering ballistic coefficient. There are many practical problems with this, of course. Those are out of scope here.

Finally, the same sequence of plots for Titan is given in figures 13, 14, 15, and 16 below. In this case, gees and heating are very low and end-of-hypersonics altitude is hundreds of km above the surface, in a very dense and deep atmosphere. A first impression says that Titan entry could be fairly easy to achieve with very high-β vehicles, at very high direct-entry speeds, and steeply-diving trajectories. All of that needs to be explored. The Titan spreadsheet is imaged in figure 17.

Conclusions Regarding “Common Lander Designs”

A really interesting design goal here might be a “common lander” that could land on Mars, or Titan, or any of the airless low-gravity worlds. Any design that works on Mars should work on Titan, and also on the airless worlds if adequate retro thrust capability is included. (It is the one of those airless worlds with the highest escape velocity that will size that propellant requirement.) One might also design for descent only, or for descent-ascent, separately. Nuclear propulsion might make a single-stage reusable descent-ascent design possible. These are all topics for future analyses and articles.

References

1. “Atmospheric Environments for Entry, Descent, and Landing (EDL)”, C. G. Justus (NASA Marshall) and R. D. Braun (Georgia Tech), June, 2007.
2. “SAE Aerospace Applied Thermodynamics Manual”, SAE Committee AC-9, published 1969 by the Society of Automotive Engineers.
3. “Mars Exploration Entry, Descent, and Landing Challenges”, R. D. Braun and R. M. Manning, no date except latest cited reference 2006.



Figure 1 – Simplified Entry Trajectory


Figure 2 – The Trajectory Analysis and Optimization Process


Figure 3 – Earth Entry Velocity Profile vs. Slant Range


Figure 4 – Earth Entry Range and Slant Range vs. Altitude


Figure 5 – Earth Entry Deceleration Gee Profile vs. Slant Range


Figure 6 – Earth Entry Heating Traces vs. Slant Range


Figure 7 – Image of Earth Entry Spreadsheet Data


Figure 8 – Mars Entry Velocity Profile vs. Slant Range


Figure 9 – Mars Entry Range and Slant Range vs. Altitude


Figure 10 – Mars Entry Deceleration Gee Profile vs. Slant Range


Figure 11 – Mars Entry Heating Traces vs. Slant Range


Figure 12 – Image of Mars Entry Spreadsheet Data


Figure 13 – Titan Entry Velocity Profile vs. Slant Range


Figure 14 – Titan Entry Range and Slant Range vs. Altitude


Figure 15 – Titan Entry Deceleration Gee Profile vs. Slant Range


Figure 16 – Titan Entry Heating Traces vs. Slant Range


Figure 17 – Image of Titan Entry Spreadsheet Data