Manned Chemical Lander Revisit

Purpose and Scope

Purpose: to find out how different a manned Mars lander design might be, under different assumptions about the extrapolation of ballistic coefficient β to a “reasonable” lander mass. I previously assumed (reference 1) a net average trend from all prior experience. This study assumes two different trends for the US probes landing on Mars, and the historic US manned capsules that landed upon Earth.

Scope was limited to a 60 metric ton entry mass for the Mars lander, chemical propulsion with storable monomethyl hydrazine (MMH) and nitrogen tetroxide (NTO) propellants, and an ascent vehicle in the neighborhood of 3.66 meters diameter. That last dimension matches the Spacex “Dragon” capsule, which in a much-modified form, might well be the descent/ascent abort sub-vehicle for astronauts trying to land on, or return from, the surface of Mars.

Re-Analysis and Curve-Fit of β Data

The original data set was researched and combined from US Mars lander probe data in reference 2, and the results of an internet search for data concerning US historic manned capsules (see reference 3). In reference 1, those data were combined into a single average entry trend at the average exponent, used with the Apollo data as a reference scaling point. That trend is a power function on lander mass:

β = βref (mass/ref.mass)^exponent where “ref” is the mass and β at some reference design

The results from reference 1 said that a manned lander in the 60 metric ton class at entry would have a β near 1100 kg/sq.m, if the hypersonic drag coefficient was near 1.3. There are very probably two things wrong with that estimate.

(1) The average Apollo hypersonic drag coefficient was actually nearer 1.5 than 1.3 (see reference 3).

(2) The manned capsules were designed for a much-different entry environment than the probes at Mars, and with much less entry protection knowledge available back then (ca. 1960).

Accordingly, in this article, I treat the two subsets of data as separate trends, and extrapolate them separately. Amazingly enough, the two separate trends predict about the same β at 60 tons mass: near 400 kg/sq.m. This results in a much-different estimate of available volumes and diameters, for crudely the same weight statement. (Actually, the final touchdown analysis is different, because end-of-entry conditions, especially altitude, are different, leading to a revised weight statement).

The basic data for both the US Mars lander probes and the historic US manned capsules are tabulated in Figure 1 below. The calculations of entry ballistic coefficient data are tabulated in Figure 2.

Since a power-function curve fit is being employed to model β versus entry mass, the appropriate curve-fitting technique is a straight-line (slope) model on a log-log plot, as in Figure 3. The natural logarithm could have been used, but was not, for convenience with data in scientific notation. As Figure 3 indicates, these “fits” are pretty good, if two separate trends are assumed. The result of this power-function modeling in absolute units is given in Figure 4. The two fits are “pretty good” visually, referenced as they are to Apollo and the MSL (“Curiosity”).

Extrapolation to 60 Metric Ton Entry Masses

Figure 5 presents the two separate power-function curve-fits on a log-log plot, extended to very large lander masses on the right. The results appear to be identical “not very far away” at 60 metric ton entry mass. However, one should be suspicious, because every unit of abscissa extrapolation on this plot is another factor of 10 on entry mass, outside the range of known data. Further, log-log plots are not very discriminating, regardless of the logarithm base used.

This is more evident in the corresponding absolute-units plot, Figure 6. It is very clear that we really are in “new territory”, by about a factor of 10 relative to Apollo, and more still, relative to MSL. However, it is gratifying to see that the two disparate trends agree on β at that particular 60-ton entry mass. 400 kg/sq.m thus seems to be a more “reasonable” estimate of 60-ton lander β, than the earlier 1100 kg/sq.m value that was used in reference 1.

Results for Lander Design Proportions and Sizes

Assuming we want a shape with about the same “bluntness” as Apollo, and that we want a “tumble-home” conical angle intermediate between that of Mercury/Gemini and Apollo, then we want a heat shield radius/diameter ratio near 1.1-1.2, and we want a conical half-angle near 30 degrees. Those proportions are given in Figure 7. Specifying mass (60 tons), β (400 kg/sq.m), and the average hypersonic drag coefficient (1.5), sets the frontal blockage area and the diameter.

For this analysis, I used a heat shield diameter of 11.28 m, and a heat shield radius of curvature of 12.4 m. Note also that we want the Apollo-type corner radius, as this typically acts to reduce local heating at the corner. No detailed corner radius was specified in this analysis, just the existence of one.

The ascent vehicle diameter shown in figure 7 is arbitrary, except that we would like this to match an existing capsule that might provide some kind of abort capability, during both descent and ascent. The value shown matches the Spacex “Dragon”, which in a much-modified form, might fulfill this role.

The conceptual internal layout of such a lander concept is given in Figure 8. The main weight-saving idea here is to use the ascent vehicle engines as the descent engines, just “sucking” from a separate descent propellant supply during that phase of flight. A wide range of engine throttleability will be required, but this has already been demonstrated to be technologically feasible. A part of the conical volume around the ascent vehicle will contain descent propellant, the rest may contain cargo, supplies, and equipment, that are to be delivered to the surface.

Such a lander comprises a heat-shielded conical descent shape with a “pointy” core (the ascent vehicle) sticking out on-axis (so that the pilots can see around themselves). Within a limited range of angles-of-attack (perhaps +/- 15 degrees), lifting entry trajectories may be flown, although, that capability is not assumed herein, for crude-overall design analysis purposes.

Unmanned cargo landers do not necessarily share this “pointy core” sticking out past the basic 30-degree cone shape, and thus may be capable of more lifting-maneuver capability during entry (near a full 30 degrees angle of attack). That can only contribute positively toward precision landings near a homing beacon.

The ports through which the engines fire must be opened, before the engine thrust deceleration can be used to provide a reliable separation of the heat shield in the face of the oncoming supersonic wind blast. This is also shown in Figure 8. Auxiliary solid propellant cartridge motors may be needed to safely effect this separation, also a well-proven technology. The MSL heat shield was about 1.6 inches (4.1 cm) thick. Using that thickness at a specific gravity of about 1.5, there are about 6.1 tons of silica-phenolic-like ablative in that heat shield. With support structures and separation equipment, a guess of 6.5 to 7 tons for the 11.28 m diameter heat shield assembly is not unrealistic. This is much larger than the 2 ton heat shield in reference 1, primarily due to the much larger diameter.

“Back-of-the-Envelope” Entry Re-Analysis

The 2-D Cartesian approximation of entry dynamics and convective heating is given in Figures 9 through 13 below. These are not a lot different from prior results except that the end-of-entry altitude (based on Mach 3 speed) is quite a bit higher at the lower β. In this case, end-of-entry is nearer 17.2 km altitude. This is still well below the 25-30 km probe experience, but much higher than the terminal altitude reported in reference 1. This required a new analysis of rocket braking to touchdown.

The basics of this entry analysis were reported in reference 2, and updated by me in reference 4 to spreadsheet integrations of total convective heat load. This analysis is adequate for orbital and direct entry estimates at Mars, but not for aero-braking calculations. This is a 2-D Cartesian approximation of entry (only) at a fixed path angle to the local horizontal. It was adequate for warhead re-entry dynamics ca. 1956. Entry calculates as 1425 s (23 minutes and 45 seconds) from entry interface to the Mach 3 point.

Rocket Braking to Touchdown

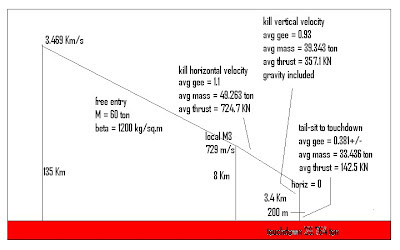
The analysis here is similar to that of reference 1. Entry requiring heat protection is assumed “done” at Mach 3, as before. This velocity is at the same 1.63 degrees entry from low Mars orbit as in reference 1, leading to a vertical velocity component of 19 m/s, and a horizontal velocity component of 675 m/s. Touchdown analysis is done with zero drag forces assumed, due to the presence of retro thrust plumes that reduce drag further than expected, by at least a factor of 2, as discussed in reference 3, and also the extreme low density of the Martian atmosphere. There is no attempt made to use an aerodynamic decelerator, as was discussed in reference 1, due to very stringent time constraints.

Vertically, velocity is accumulated downward due to Mars gravity as the vehicle makes a burn (parallel to the local horizon) to kill all the horizontal velocity component. This is arbitrarily done so that the altitude at which the horizontal velocity zeroes is half the terminal entry altitude (which sets the average deceleration level). Thrust levels are set by that deceleration level, only in this phase.

Then the vehicle pitches up vertical (engines still burning) and kills all the accumulated vertical velocity but an arbitrary-but-“reasonable” 20 m/s, by the time it reaches the “reasonable” altitude of 200 m. Thrust levels are set by the net (or effective) deceleration plus average weight in this phase.

From there, it descends at an average 10 m/s to the surface (20 m/s to zero in 200 m). In this phase, thrust is very nearly equal to weight. The propellant mass expelled in this phase is quintupled in the design, to provide a terminal maneuver capability of around 100 seconds in order to avoid obstacles.

In each of these three phases, the velocity change is used in the rocket equation to estimate mass ratios and masses at the end of each phase. Mass changes correspond to propellant masses used. The average mass at the average net acceleration gives the base thrust, to which vehicle weight must be added in the two vertical phases.

Velocity, altitude, and mass information for this rocket-braking descent are given in Figure 14. The mere 144 sec interval from Mach 3 to touchdown makes it quite clear why aerodynamic decelerators are not feasible for this kind of a landing. Most parachutes cannot be deployed above about Mach 2.5 speeds, and simply could not decelerate the vehicle subsonic before impact. So there is no point.

Ascent Requirements (Basically Unchanged from Reference 1)

For this analysis, the crew capsule was assumed to be 5.5 metric tons, about halfway between the mass limits used in reference 1. The modified Dragon would be the capsule with a thinner, lighter heat shield, extra propellant on board, and no trunk module. It would carry at most 3 men, plus enough propellant to land on the Super Draco thruster system, without landing legs. No parachute is assumed for the abort scenario, nor were any of those abort scenarios analyzed in detail here.

That crew capsule was assumed to ride as “payload” atop a single-stage MMH-NTO rocket of the same 3.66 m diameter, of 5% inert mass ratio, as has been demonstrated recently for throw-away vehicles. These design requirements are summarized in Figure 15. This is an ascent vehicle capable of reaching LMO, but with zero plane-change capability. It represents the minimum that could (or should) be done. Adding plane change delta-vee increases the size and mass of this ascent vehicle. Big enough, and the entry mass of the lander must be increased, as you quickly go negative for your cargo allowance.

Per the data and methods of reference 5, the absolute minimum theoretical velocity requirement to reach 200 km LMO without plane change is 3.455 km/s. The “traditional” gravity loss on Earth has been about 5% of theoretical velocity. The “traditional” drag loss for a slender vertical launch rocket has been about 5% of theoretical velocity here on Earth. Scaling the gravity loss down by 0.38 gee, and the drag by 0.7% surface density, at Mars, results in a combined gravity-drag loss factor of 1.94% for Mars. Add another 2.7% for design margin, for 3.62 km/s delivered delta-vee, as long as the plane change is zero.

The stubby shapes for the lander considered here probably have twice the normal ascent drag coefficient, but twice near-nothing is still close to nothing. That issue is more properly explored with a real computer trajectory code.

Ascent Vehicle Dimensions and Masses

The ascent vehicle as re-sized is depicted in Figure 16. This vehicle is far shorter than was expected, so that a serial arrangement of fuel and oxidizer tanks is nearly all elliptical head spaces and very little cylindrical space. The appropriate propellant volume-to-cylindrical envelope volume factor is thus probably lower than the 90% that I used. Propellant density data were obtained from reference 6.

However, a lower limit for simple packed spheres is 63%, so we cannot be all that far off. I rounded up my tank length results to compensate a bit for this effect. The capsule and the wild guess for engine length dominate ascent vehicle length, anyway. This is because of the 3.66 m diameter.

Accordingly, a parallel arrangement of fuel and oxidizer tanks is more likely the “best” design choice. There would be only two elliptical heads, with radial bulkheads separating fuel and oxidizer. These tanks would have to be equally pressurized, so that the straight radial bulkheads are structurally practical. Either way, the overall vehicle length is probably not all that far from the value depicted.

For the ascent design, the mass ratio MR is computed from the delta-vee required and the estimated exhaust velocity. The propellant mass fraction (in this case just under 71%) is

PMF = 1 - 1/MR

The payload is a fixed mass at about 5.5 tons, as “guessed” for a Dragon capsule modified for extra propellant and a lightened heat shield, but without its trunk section. The inert (structural) mass fraction (IMF) is assumed to be 5%, as has been demonstrated operationally in throwaway rocket vehicles. This would include the engines as well as the tankage structure.

The payload mass fraction available is 1 minus the propellant and inert fractions, in this case a bit over 24%. The payload mass divided by the available payload mass fraction sets the ignition mass for the ascent vehicle, in this case, not quite 23 metric tons. For storable propellants, it is clear that this ascent can easily be done in a single stage vehicle, as long as orbital plane changes are not required.

As far as the lander is concerned, the entire ascent vehicle is “dead-head payload”, with the exception of the engines themselves. Those engines will “suck” descent propellant from tanks inside the lander, but outside the ascent vehicle.

The study in reference 1 did not compute volumes and lengths for the ascent vehicle, only a weight statement. The shortness of the ascent vehicle obtained here impacts the actual final shape of the descent vehicle, as described in the next section.

Manned Lander Weights and Volumes

I had been expecting a long ascent vehicle to “stick out of” a 30-degree tumble-home conical descent shell. Instead, the ascent vehicle turned out to be quite short. For practical pilotage reasons, as well as safe abort reasons, it is necessary that the crew cabin capsule be located outside the descent shell. Accordingly, I went to a double cone shape not unlike that of the unmanned US Mars probe lander aeroshells.

The construction concept here is a base frame to which an aeroshell frame is attached. The aeroshell panels are attached to those frame elements, and fold down to provide a second function as unload ramps. The base frame supports a segmented heat shield below, and mounts the ascent vehicle above. Inside this shell are 3 or 4 landing legs, extended laterally, then axially, to provide engine clearance.

The volume enclosed by this aeroshell contains both descent cargo and the descent propellant tanks. Again, there is a lot more volume available inside this shell than any conceivable configuration of descent propellant tanks could ever require. Thus, there is plenty of room for lots of very low-density cargo. See Figure 17 for the final dimensions and weight statement.

Note that this analysis indicates that the 3 astronauts could reach the surface of Mars with over 5 metric tons of supplies and equipment. That is quite a remarkable result, especially since it is seemingly easily reached by eliminating the aerodynamic decelerator in favor of simple rocket braking. Note that no retro thrust is required during hypersonic entry in this design, only during the supersonic-to-subsonic deceleration, post-entry.

Unmanned Variant Weights and Volumes

The same basic aeroshell and heat shield could enclose the same set of engines mounted directly to the same base frame, and drawing from the same kind descent propellant tanks, just placed differently. In this case, the rest of the ascent vehicle is deleted in favor of more cargo mass, for which there is plenty of available volume. This unmanned cargo lander design is depicted in Figure 18. Note that the cargo deliverable to the surface is over 28 metric tons, from the very same 60 ton entry mass.

Conclusions

Large lander vehicles capable of taking 3 astronauts to the surface of Mars might have ballistic coefficients nearer 300-500 kg/sq.m than the 1000-1200 kg/sq.m indicated in reference 1. This change in assumptions affects the detailed numbers, but not the primary outcome: landing large payloads on Mars is not nearly as hard, as has been recently hyped.

The time between end of entry at Mach 3 and surface touchdown is far too short for aerodynamic decelerators to deploy, much less be effective, at ballistic coefficients over about 200-300 kg/sq.m. This is because the end-of-entry altitude is so much lower at the higher ballistic coefficients. Therefore, the preferred approach at high β is to go directly from heat-shielded entry to direct rocket braking for touchdown.

This change in design paradigm turns out to be very feasible for landing crews of 3 with around 4-5 tons of equipment and supplies, in a lander massing no more than about 60 metric tons at entry, while using easily-storable chemical propellants.

The ascent vehicle in this design is of minimal size for no plane change capability. Adding plane change capability adds considerable mass to the ascent vehicle, and also to the descent vehicle that carries it to the surface, in a compounded manner. If plane changes are required, this may be better done by the carrier vehicle in LMO that is launching these landers.

References

1. G. W. Johnson, “Chemical Mars Lander Designs ‘Rough Out’”, posted 8-12-12 to http://exrocketman.blogspot.com

2. C. G. Justus and R. D. Braun, “Atmospheric Environments for Entry, Descent, and Landing (EDL)”, MSFC-198, June, 2007. (Model atmospheres and a description of the 1956-vintage entry analysis)

3. G. W. Johnson, “Blunt Capsule Drag Data”, posted 8-19-12 to http://exrocketman.blogspot.com

4. G. W. Johnson, “Back of the Envelope Entry Model”, posted 7-14-12 to http://exrocketman.blogspot.com (1956-vintage entry analysis updated and adapted to spreadsheet)

5. G. W. Johnson, “Big Mars Lander Entry Sensitivity Study”, posted 8-10-12 to http://exrocketman.blogspot.com (done for entry from LMO at 200 km)

6. Pratt and Whitney “Aeronautical Vest-Pocket Handbook” 12th edition, 21st printing, December, 1969.



Figure 1 – Basic Physical Data


Figure 2 – Computed Ballistic Data


Figure 3 – Curve-Fitting Prior Data on a Log-Log Plot


Figure 4 – Quality of the Two Separate Curve Fits Appears “High”


Figure 5 -- Extrapolation of Both Curve Fits on a Log-Log Plot


Figure 6 -- What Those Extrapolations Really Look Like In Absolute Units


Figure 7 – Lander Design Proportions


Figure 8 – Internal Layout Concept for Lander


Figure 9 – Selected Spreadsheet Images for Entry Analysis


Figure 10 – Entry Results: Velocity vs Slant Range


Figure 11 – Entry Results: Range and Slant Range vs Altitude


Figure 12 – Entry Results: Deceleration Gees vs Slant Range


Figure 13 – Entry Results: Convective Heating vs Slant Range


Figure 14 – Terminal Dynamics Results (Entry to Touchdown)


Figure 15 – Assumptions Made Regarding the Ascent Vehicle


Figure 16 – Final Weights, Dimensions, and Volumes for Ascent Vehicle


Figure 17 – Final Weights and Volumes for Manned Lander


Figure 18 – Final Weights and Volumes for Unmanned Cargo Lander

Ballute Drag Data

Scope and Purpose

For landing upon any world with a significant atmosphere, the drag of an inflatable ballute is of considerable interest. This includes both Earth and Mars, as well as Titan and Venus, and further the giant planets. Drag during the later phases of entry is as much a topic of interest as post-entry supersonic drag. This is because ballutes might possibly reduce the ballistic coefficient of probes or landers during hypersonic entry, if the hypersonic heating problem can be handled.

Sources

I found some ballute data as a function of shape at one (and only one) Mach number in reference 1. For only one of these basic shapes, there was also an indication of drag coefficient as a function of supersonic Mach number, although this was at a slightly different cone half-angle for the conical portion.

Results

Figure 1 presents the basic results for three different shapes at one Mach number (4.0) from reference 1. The drag coefficients for these are not very different. The same reference gave drag versus Mach for one of these shapes (Table 1), although not exactly the same shape as any one of the three (a slightly-higher conical half-angle).

Conclusions

As an average curve versus Mach, use the data in Table 1 as a reference value. For your shape, scale that curve up or down according to the drag coefficient data of figure 1.

The effect of cone angle for the cone-sphere shape upon drag coefficient is about 2.5% per degree of conical half-angle, within the data range 38 to 40 degrees. You can probably extrapolate outside that range by +/- 5 degrees with relative impunity, in my humble opinion.

As usual, drag coefficient is referenced to the blockage (or frontal) area, in this case, 0.25*pi*dia^2

References

1. Sighard F. Hoerner, “Fluid Dynamic Drag”, self-published by the author, 1965.


Figure 1 – Ballute Drag Data vs Shape and Tow Distance (updated to correct D1/L error to L/D1)

Blunt Capsule Drag Data

Purpose and Scope

Data from both Mercury and Apollo were combined here as a “database” for guessing fairly closely the hypersonic drag coefficient of a blunt capsule shape. A drag curve for a shape like Mercury from subsonic to Mach 24.5 was found in one old textbook, presumably based upon wind tunnel data. Data for Apollo-like shapes was found at selected Mach numbers in another old textbook. These were definitely old wind tunnel data. The intent here is to find a range of drag coefficients and average values suited to the Mach 3 to Mach 25 range of hypersonic flight.

Sources

Reference 1 (Miele) had a good graph of drag coefficient versus Mach number for a Mercury capsule shape. That graph was read and input into an Excel spreadsheet for purposes here. There were no specific attributions on that graph to actual wind tunnel data, although that was the implication in context.

Reference 2 (Hoerner) had data at selected Mach numbers for both the Mercury and Apollo shapes, with a range of “tumble-home” angles on the Apollo shape. The reference indicated cited actual wind tunnel data.

Geometric data for both capsules was found after a brief internet search, which pinned down the actual Apollo tumble-home angle, and defined the heat shield radius to diameter (bluntness) ratios for both capsules.

It should be noted that the Mercury shape was fairly “sharp" transitioning from the blunt heat shield to the tapered (tumble-home) afterbody. Apollo had a generous radius at that transition, which does affect the location of the sonic line and subsequent flow field around the afterbody.

Results

The Miele curve for Mercury is given in Figure 1 below, with the Hoerner Mercury and Apollo data spotted upon it. At Mach 4.5, the Miele curve and Hoerner’s Mercury data are the same, probably because they are really from the same test data. The Apollo data from Hoerner are generally very slightly above the Miele curve for Mercury. Over the range of Mach 3 to 25, the average drag coefficient of the Mercury shape is 1.45, while Apollo is 5 to 10% higher at about 1.55.

The two capsule shapes are compared in Figure 2, along with a sketch of the general flow field features. Hypersonically, we would expect that the blunter the object, the higher the drag coefficient. Bluntness is measured by the heat shield radius of curvature to diameter ratio. Apollo has a comparable, but slightly higher, bluntness as shown. The reference area for drag coefficient is, in all cases, the frontal or blockage area of the shape:

A = 0.25*pi*(diameter)^2

The radius of curvature at the transition from heat shield to tapered afterbody would be expected to influence overall drag by its effects on the sonic line location and separated flow zones, and their effects on the strength of the trailing shock wave.

The “tumble-home” angle of the tapered afterbody would also be expected to influence overall drag by its relation to the available Prandtl-Meyer expansion turning angle downstream of the sonic line. This affects both surface pressure coefficient and trailing shock strength. Larger tumble-home angle allows greater angle of attack for lifting during entry, without exposing the tapered side wall to “direct” hypersonic windblast and heating.

For either variable (local radius or “tumble-home”) these effects do not act all in one direction, and they most definitely interact in a very complicated way. For the Apollo shape, Figure 3 clearly shows that increasing the tumble-home angle effectively acts to decrease overall drag.

Conclusions

An educated guess says that the bluntness (radius to diameter ratio) effect is stronger than the 5-10% increase in drag seen here, for Apollo to relative to Mercury. It is apparently offset in part by the more generous transition radius on Apollo, which lets the sonic line occur further downstream, and reduces the Prandtl-Meyer expansion effects, in turn weakening the trailing shock. This would act to decrease drag. Thus the two curves are “close”. The net effect says that Apollo is probably pretty close to Miele’s Mercury curve, just factored up by about 1.07.

Another educated guess says that increasing the tumble-home on the Apollo shape seems to “suck” that sonic line further downstream. This apparently has the effects of lowering the imposed flow turning angle, weakening the Prandtl-Meyer expansion, raising the surface pressure coefficients, and lowering the oncoming Mach number for the trailing shock. This is reflected in lower drag at more tumble-home, and higher drag with less, as shown in Figure 3.

For an Apollo shape, I recommend factor 1.04 drag increase for 5 degrees tumble-home decrease, and factor 1.07 decrease for 5 degrees more tumble home. You could very likely use this same sensitivity on data for a Mercury shape, and not be too far off. But the Mercury data will not directly correlate, due to the effects of the different transition radius. This is shown dramatically in Figure 3, where the actual Miele Mercury data are drag coefficient 1.27 at Mach 24.5.

Use tumble-home drag sensitivities of 0.8% increase per degree below reference, and 1.4% decrease per degree above reference, for figuring changes from the baseline Apollo shape at reference tumble-home 34 degrees. You could probably get away with using this same correction referenced to 20 degrees tumble-home, on the basic Mercury shape, although there is no real data here to actually support that action.

For capsule shapes that have a sharp transition and about 20 degrees tumble-home, use the Miele Mercury curve as it is, which corresponds to an average 1.45 hypersonic drag coefficient for the Mach number range from 3 to 25. Then adjust it for tumble-home effects different from 20 degrees.

For capsules with a radiused transition and about 34 degrees tumble-home, use the Miele curve factored up by about 1.07 as it might represent Apollo. This would average 1.55 from Mach 3 to Mach 25. Then adjust that for tumble-home effects different from 34 degrees.

References

1. Angelo Miele, “Flight Mechanics”, published by Addison-Wesley, 1962.
2. Sighard F. Hoerner, “Fluid Dynamic Drag”, self-published by the author, 1965.


Figure 1 – Blunt Entry Capsule Hypersonic Drag Data


Figure 2 – Blunt Entry Capsule Shape Comparison


Figure 3 – Capsule “Tumble-Home” Angle Effects

Third X-51A Scramjet Test Not Successful

Update 5-4-13:

X-51A test 4 (the final one) was successful.   4 minutes burn followed by 2 minutes coasting-down flight.  Hydrocarbon-fueled scramjet burn at Mach 5.1.  Compare that to ASALM-PTV flight test 1 of 7:  accidental acceleration to Mach 6 on hydrocarbon fuel at only around 20,000 feet.  ASALM-PTV was an ordinary ramjet,  not a scramjet.  This was done back in 1980.
---------------------------------------------------------------------
Original article:
---------------------------------------------------------------------
Various news stories have given the results of three X-51A Waverider tests so far, of 4 vehicles built. The third ended in failure quite recently. So did the second last year (2011). The year before (2010), the first test was a 140-second long success, accelerating through Mach 5 after rocket boost.

The vehicle is a “waverider”, meaning it rides on the pressure of its own bow shock acting on its belly for lift. It is rocket boosted to about Mach 4.5, then “takes over” with a JP-7-fueled supersonic-combustion ramjet (scramjet) engine. It is designed to test scramjet technology in the Mach 4.5 to 6.5 range, according to Boeing, who built it as a joint venture with Pratt and Whitney Rocketdyne for USAF.

Earlier Scramjet Flights

The previous scramjet test effort reported in the news was NASA’s X-43A, of which 3 were built. That vehicle was hydrogen-fueled.

The first test in 2001 ended in failure. The second test in 2004 demonstrated thrust enough to climb slightly at a little under Mach 6.8, for about 10 or 11 seconds. The third and final test , also in 2004, demonstrated scramjet acceleration at about Mach 9.8, also for about 10 or 11 seconds.

It was that Mach 6.8 test in 2004 that broke the previous speed record of Mach 6 held by an aircraft powered by airbreathing propulsion. The third test’s speed record of Mach 9.8 still stands.

Scramjet Technology

Scramjet is a very difficult technology to “tame”. It has been undergoing serious ground tests of various kinds since the early 1960’s. Very careful attention must be paid to balancing the engine and inlet with appropriate ducting. The scramjet takeover speed is necessarily very high: at least Mach 3.5 or 4, which requires an enormous rocket boost. Another problem is the extreme friction heating with external and internal airflow at those speeds. Yet another is the enormous difficulty of injecting and mixing the fuel into the supersonic inlet airstream, without inducing huge shock wave and flow-separation losses.

One of the selling points made for investigating this kind of propulsion is very high speed missile applications, such as “the ability to carry out a military strike anywhere in the world in less than 60 minutes”. Another might be propulsion for a space plane. But, as the two series of flight tests so clearly demonstrate, this technology is still very far from being ready for application.

Some History

Back about 1980, a technology-demonstrator flight test vehicle called ASALM-PTV accidentally accelerated to Mach 6 at 20,000 feet on its very first flight test. This was due to a fuel control “failure” that was nothing but a stupid assembly error, there was nothing really wrong with the design. It was only designed to cruise at Mach 4, and to power-dive at Mach 5. The other 6 flights were perfect. Its design mission was as a cruise missile effectively invulnerable to defense: subsonic launch, supersonic climb to 80,000 feet (24 km), pullover and accelerate to a Mach 4 cruise, then suddenly dive at Mach 5 onto target.

ASALM was not scramjet at all, it was just an ordinary subsonic combustion ramjet, with part of its technological roots dating all the way back to World War 2. It had a supersonic inlet, a large but mild-expansion nozzle, and a dump combustor for its flame stabilization. It was fueled with RJ-5, a synthetic strongly resembling kerosene.

Unlike the two scramjets, ASALM had an “integral booster” packaged entirely within its engine, not a huge booster stage out behind, to be dropped off. The takeover Mach number with ASALM was Mach 2.5, so the booster could be much smaller in any event.

It was not a waverider, but it did fly on supersonic body lift without any wings. ASALM had a very clean, low-drag "dart" shape, which is a part of how it accidentally reached Mach 6 in that runaway test flight.

I got to work on several related technology projects associated with ASALM, and to participate in the engineering done around the booster inside that combustor. A lot of the same technology went into other ramjet engines I worked on.

The NASA X-43A guys named ASALM as the setter of the record they finally broke in 2004, but they didn't know what ASALM was, or what kind of engine it had. I guess they were just too young: ASALM was well before their time.

Opinion

USAF's design mission for that scramjet missile technology could be done easier, cheaper, and "right now" by marrying existing ICBM technology with existing ramjet cruise missile technology (like ASALM). Put your supersonic ramjet cruise missile inside a re-entry shroud, and stick that on top of an ordinary ICBM. Flight time is 17 minutes to the other side of the world, then you cruise to target in the Mach 3 to 4 range, at around 60-80,000 feet, and finally you dive onto your target at around Mach 5 to 6. If you are attacking fixed geographic coordinates, there is not time for simple inertial guidance to drift.

As I said before, simple. Easy. Cheap.

My question to USAF is: why cruise hypersonic down in the air with all that friction heat and shock loss nonsense, when you don't have to? Actually, the very same question applies to supersonic/hypersonic transport aircraft proposals, too.

GW

Update 9-11-13:  The 4th and final X-51 flight was successful. 

Chemical Mars Lander Designs “Rough-Out”

Purpose and Scope

This is a rough estimate of what might be done for landing men (two-way) or cargo (one-way) on Mars, with as common a set of hardware, as is practical. These are ballpark pencil-and-paper calculations. They serve as good start-points for investigators that have access to appropriate trajectory computer programs.

Entry is assumed to be from circular orbit at 200 km altitude, by minimum de-orbit burn conditions. Direct entry from Hohmann transfer orbit conditions (or any other transfer orbit conditions) is NOT covered by these results.

Entry conditions are limited to 3.469 Km/s velocity at 135 Km interface altitude, with a trajectory depression angle of 1.63 degrees. Both the manned and unmanned vehicles are assumed to have hypersonic ballistic coefficients of 1200 kg/sq.m, with no retro thrust during the entry hypersonics.

Under these assumptions, end-of-entry conditions are 8 Km altitude at local Mach 3, nominally 729 m/s, 1.63 degrees depressed below horizontal. Because of the low altitudes at end-of-hypersonics, it is assumed that no chutes or ballutes are used. There is simply not time and room for these to deploy or to be effective. Landing is by retro thrust only.

Methods

End of simple ballistic hypersonic entry at local Mach 3 is assumed as the start-point for these calculations, per the results of reference 1. The ballistic coefficients of the manned and unmanned landers are assumed to be equal at 1200 kg/sq.m, per the results of reference 2, for vehicles in the 60 metric ton class at entry.

Post entry, it is assumed that the pilot (or autopilot) pitches the vehicle to zero angle with respect to local horizontal, and makes a burn to “kill” all the horizontal velocity. This presumes that vertical velocity will increase under gravity. In actuality, a real pilot will angle his burn slightly downward to “kill” the vertical gravitational acceleration as well, but the net effect is very nearly numerically equal.

This has to be done at a high-enough gee level to reduce the gravity-induced vertical velocity and descent distance to acceptable values. Here, those were merely “judgment calls” at time intervals around 1 minute, so that final altitude was “close” to half the initial value. An average constant acceleration approach was used to relate velocity increment to distance covered (and the resulting time). The basic delta-vee was by simple rocket-equation estimation, leading to end-of-interval vehicle masses and propellant-consumed masses.

Once the horizontal velocity is zeroed, there is a residual vertical velocity needing to be zeroed by the time a “practical” altitude is reached. This final altitude was arbitrarily set at 200 meters. The same kind of rocket-equation delta-vee was used, with thrust levels raised by one Martian gee (0.381 Earth gee) to offset the vehicle weight, since orientation is now vertical. Again, average acceleration and average mass levels set the thrust, via the constant average acceleration assumption.

From 200 m, the vehicle is a “tail-sitter” on its own thrust vector at low velocity. The average transit velocity downward must be fast enough to save fuel, but slow enough to be practical. A triangular waveform is the easiest to “analyze”. An average 10 m/s downward was used here, rather arbitrarily, in order to limit total propellant burn. Peak downward is 20 m/s, with 0 m/s at each end of the interval.

For the rocket equation, MMH-NTO propellants were assumed, but with engine cant angle 10 degrees lowering the effective specific impulse. This aids plume and flowfield stability while still supersonic. A short expansion bell, possibly scarfed, was also assumed, for packaging geometry reasons. The net result was lowering a short-bell 305 sec specific impulse to a canted 300.4 sec specific impulse. The effective exhaust velocity for the rocket equation is then pretty close to 2946 m/s.

For the manned lander case, there must be an ascent vehicle capable of returning to LMO, without plane changes (same assumption as for descent). It is also assumed that the same engines serve for ascent as served for descent. The empty descent propellant tanks, cargo, aeroshell, and associated framing structure are left behind. The heat shield is assumed to be “blown away” explosively in segments, at end of hypersonic entry. This vehicle has landing legs and a bottom frame structure. Inert mass fraction is assumed to be near 10%.

For the unmanned, one-way cargo lander, there is no ascent vehicle. That mass allowance goes into deliverable cargo within the aeroshell. All else is the same.

For the manned ascent vehicle, it is assumed that there are three men in a nominal crew. These men ride in a capsule that needs ascent abort capability, so that they might be rescued using a second lander. Thus, the crew cabin capsule should have at least 4 seats, for the rescue pilot, plus the crew of 3 needing rescue. Such a crew cabin capsule might resemble a stripped-down Spacex “Dragon” without the unpressurized trunk (service) module. Herein, a capsule mass in the 4-5 ton range was assumed.

Basic Trajectories

See Figures 1 and 2 below. Per reference 1, peak entry deceleration gee level is about 0.7 standard (Earth) gees. There is no retro thrust during hypersonic entry. At end of entry (about local Mach 3), the 2-ton heat shield is jettisoned as several segments, and the engines (4 to 6 of them) are started. Horizontal velocity is “killed” at about 1.5 standard gees average retro thrust, while at worst, the vertical velocity is allowed to accumulate gravitationally.

The vehicle pitches up vertical, at no horizontal velocity, in the vicinity of 3.4 Km altitude, with at worst about 185 m/s vertical downward velocity. This vertical velocity is “killed” at about 0.9 standard gees deceleration retro thrust, with a terminal altitude near 200 m.

From that altitude, thrust is varied about the weight value at a nominal 0.381 standard gees. Initially, thrust is cut and the vehicle allowed to accelerate downward. This is followed by a thrust throttle-up to kill all vertical velocity, just as the vehicle touches down.

Basic rocket propulsive characteristics are given in Figure 3.

The ascent trajectory is illustrated in Figure 4. This was figured from the rocket equation, factored to allow for gravity and drag losses on a fast-ascent trajectory with a slender vehicle. Gravity losses were factored down by Martian 0.381 gee from “the usual 5%”. Drag losses were factored down by the Martian 0.7% density ratio from “the usual 5%”. Net velocity increment factor was thus 1.0194.

Results – Manned Lander

The manned lander was figured with an ascent vehicle whose crew cabin capsule masses 4 to 5 metric tons. This capsule needs an ascent abort capability, rather like a Spacex “Dragon” with the Super Draco thrusters and some landing legs. It would have to be substantially stripped-down, and without a trunk section (service module). Depending on whether this capsule was 4 or 5 tons, there is room to carry 2 to 6 metric tons of cargo from LMO to the surface. This would include any rover car, exploration equipment, surface “inflatable Quonset hut” habitat, and life support supplies for the landing duration. The crew of 3 is included in the mass of the ascent vehicle (and in that crew capsule). See Figure 5. The aeroshell sectors fold down to double as unloading ramps.

Results – Unmanned Cargo Lander

The one-way unmanned cargo lander uses the same engines, but these are mounted directly on the descent frame, without any ascent vehicle. The ascent vehicle mass adds to cargo capacity, which is then pretty close to 25 metric tons. Most of the descent propellant is packaged where the ascent vehicle would have been. See Figure 6. Like the manned vehicle, the aeroshell sectors fold down to double as unloading ramps.

Update 8-13-12

Revised Figure 5 to show corrected structure weights on ascent and manned descent vehicles. Added Figure 7 to give weight statements and miscellaneous data. Note that the structural weight of the descent vehicle is rather low. The most-likely-needed added structure, whatever it might be, will have to come out of the cargo weights. The 5-ton crew capsule on the ascent vehicle thus looks more attractive.

References

1. G. W. Johnson, “Big Mars Lander Entry Sensitivity Study”, posted 8-12-12 on http://exrocketman.blogspot.com.

2. G. W. Johnson, “Rough Correlation of Entry Ballistic Coefficient vs. Size for “Typical” Mars Landers”, posted 7-25-12 on http://exrocketman.blogspot.com.



Figure 1 – Basic Lander Trajectory Data


Figure 2 -- More Trajectory and Vehicle Data


Figure 3 – Propulsive Assumptions and Data


Figure 4 – Ascent Requirements


Figure 5 – Manned Lander with Ascent Vehicle, Same Engines


Figure 6 – Unmanned One-Way Cargo Lander, Same Heat Shield, Frame, and Aeroshell


Figure 7 - Weights and Miscellaneous Data

Second Update 8-16-12

I forgot to clarify exactly how I did those post-hypersonic trajectory estimates. I considered the velocity changes required as compared to rocket equation delta-vee, including vertical increments due to gravity. I did not include any corrections for the retarding force of aerodynamic drag, for three reasons: (1) not including drag effects puts more margin into the required rocket equation delta vee, (2) drag is already a smaller force compared to weight or inertia forces on Mars due to the thin atmosphere (see deceleration gees at Mach 3 from the entry data), and (3) there is good reason to believe that a retro-thrust jet into the oncoming supersonic slipstream will cut drag to about half of the no-thrust value.

Just post Mach 3, the basic idea is to zero out the dominant horizontal velocity component. Effectively, I just zeroed-out the entire velocity component, setting velocity at Mach 3 equal to the rocket delta vee required. There was no corrective weight term included in the corresponding thrust. This has to be done in a reasonable time (which sets that thrust level), such that the end-of-interval altitude is still acceptable. That altitude is set by the gravitational free-fall during that interval.

Without a weight-cancelling force, the vehicle accelerates downward at Martian gravity acceleration, even as it decelerates horizontally. End of hypersonics was 8 km nominally, and about 3 to 4 km at zero horizontal velocity seemed “reasonable” to me. The resulting vertical velocity build-up must then be cancelled. It is equal to the new rocket delta-vee, but the net acceleration-induced thrust level corresponding to it must be increased by vehicle weight, to achieve this type of motion in vertical flight. That net vertical deceleration must further terminate at a “reasonable” altitude for beginning the “tail-sitter” descent phase. I picked an arbitrary 200 meters for that altitude.

The final “tail-sitter” portion of the descent must average a reasonable pace, or else too much propellant is burned. My numbers were pretty arbitrary at 10 meters per second average, in a triangular waveform peaking at 20 meters per second, with 0 meters per second at each end. The time to descend (in this case 20 seconds) sets the total impulse, and therefore the propellant burn. Thrust levels will be variable, but very close to vehicle weight on Mars.

The reason to believe that retro thrust reduces drag is from the old Sighard F. Hoerner “Fluid Dynamic Drag” book, which he published himself about 1965. In the Chapter 20 “Practical Results” section, there is a wind tunnel data plot in his figure 27 for a Mercury capsule-like shape in supersonic flow, with a retro thrust jet simulated by high pressure air. For a retro thrust coefficient of 0.16, drag coefficient was slightly less than half the zero-thrust value. That retro thrust coefficient was retro thrust force divided by the product of dynamic pressure and frontal blockage area, similar to drag coefficient.

For the ascent vehicle, I did include gravity and drag effects in a simple factor that knocks down delta vee from the rocket equation value. I typically use 5% gravity loss and 5% drag loss for slender vertical launch rockets here on Earth. Those I ratioed-down by Mars gee (0.381) on gravity, and Mars surface density ratio to Earth standard (0.007) on drag. The knockdown factor so obtained is 1.0194.

Direct-Entry Addition to Mars Entry Sensitivity Study

Purpose and Scope

This is an addition to reference 1 to cover direct entry from Hohmann transfer to Mars. The purpose is to define, for the average direct entry case, a typical altitude for end-of-hypersonics at local Mach 3. It presumes the same shallow entry angle of 1.63 degrees as the minimum de-orbit burn from low Mars orbit at 200 km. It also presumes the same nominal ballistic coefficient of 1200 kg/sq.m, thought to be representative of a 60-ton manned lander. All other conditions are the same as in reference 1.

Velocity requirements for Hohmann transfer to Mars were defined in reference 2. The typical departure velocity in LMO is pretty close to the entry interface velocity. For the average case, that is 5.55 km/s. Velocity increases a little as altitude decreases, so a nominal 5.6 km/s was used here to see the effects of a realistic higher velocity. This is not the worst case, but it is “typical”.

Methods

These are identical to reference 1, being the 2-D Cartesian “back of the envelope” entry model used in reference 1. This was adapted and updated from a 1956-vintage model, as reported in reference 3. A spreadsheet form was used here, the same as in reference 1.

Results

Increasing the entry speed increases deceleration gees and heating, and decreases terminal altitude, as expected. Peak gees increases from 0.7 for the nominal entry from LMO to just under 2 gees for direct entry. Terminal altitude decreases from 8 km nominal to about 5.5 km for direct entry. Worst case entry velocity would penetrate even lower, raising the possibility of needing rocket braking during, not just after, the entry hypersonics.

A collage of spreadsheet spreadsheet images is given in Figure 1, below. The entry velocity vs slant range trace is given in Figure 2. The range and slant range traces vs entry altitude are given in Figure 3. The deceleration gee trace vs slant range is given in Figure 4. The stagnation-point heating data traces vs slant range are given in Figure 5.

Conclusions

Direct entry makes the terminal hypersonic altitude substantially lower than that for entry from LMO. The required rocket braking to touchdown will be more demanding, and must occur during a shorter timeline. But, there is nothing here to suggest that it cannot be done.

The sensitivity to entry angle is extreme, as was already demonstrated in reference 1. As is often the case, the entry corridor will be shallow and narrow, requiring very precise trajectory control approaching Mars. That kind of trajectory control is inherent, if entering from LMO instead.

There is the possibility that rocket braking will be needed during, not just after, the entry hypersonics. This would arise if entry velocity conditions extremize further, and most especially if the entry angle steepens, even by very tiny amounts.

References

1. G. W. Johnson, “Big Mars Lander Entry Sensitivity Study”, posted 8-10-12 at http://exrocketman.blogspot.com.

2. G. W. Johnson, “Velocity Requirements for Mars Orbit-Orbit Missions”, posted 8-2-12 at http://exrocketman.blogspot.com.

3. G. W. Johnson, ““Back of the Envelope” Entry Model”, posted 7-14-12 at http://exrocketman.blogspot.com.



Figure 1 – Spreadsheet Images for Direct Entry


Figure 2 – Direct Entry Velocity vs Slant Range


Figure 3 – Direct Entry Range and Slant Range vs Altitude


Figure 4 – Direct Entry Deceleration Gees vs Slant Range


Figure 5 – Direct Entry Stagnation Point Heating vs Slant Range

Big Mars Lander Entry Sensitivity Study

Scope and Purpose

A previous study (reference 1) indicated that a manned Mars lander might be in the 60 metric ton “mass class”, and might have a ballistic coefficient in the neighborhood of 1200 kg/sq.m. Such a craft would be roughly conical at something around 7 m diameter. There is considerable uncertainty associated with that ballistic coefficient value, perhaps the plus-or-minus 500 kg/sq.m used here.

Another previous study (reference 2) used a 200 Km circular orbit about Mars as the point of departure for deorbit and entry. That path was arbitrarily selected to have a periapsis of surface impact. Orbit calculations using the recommended interface altitude of 135 Km (see reference 3), gave nominal entry conditions of 3.469 Km/s at 1.63 degrees down entry angle relative to local horizontal. These would apply to any ballistic coefficient. That de-orbit trajectory is depicted in Figure 1. The nominal de-orbit delta-vee is 50 m/s.


Figure 1 – Nominal De-Orbit Burn Trajectory

The reference 2 study found that end-of-hypersonics (at local Mach 3) occurred at relatively low altitudes compared to our previous experience with the much smaller unmanned probe landers, and that the higher the ballistic coefficient, the lower the end-of-hypersonics altitude. That effect was re-explored here, with a tighter spread of ballistic coefficients more applicable to actual vehicle rough-sizing. Providing that kind of sensitivity analysis to support lander rough-sizing is the purpose here.

It has been suggested that a way to alleviate the low altitude problem is to reduce velocity at entry interface by applying a larger rocket de-orbit burn. That effect was explored here at the nominal ballistic coefficient of 1200 kg/sq.m, with a 10-times-larger de-orbit delta vee of 500 m/s. As shown in Figure 2, orbit calculations gave the expected lower entry interface velocity, but at a considerably steeper entry angle:

Vatm = 3.029 Km/s
γ = 6.4 degrees


Figure 2 – “Big De-Orbit Burn” Trajectory

The entry model is the same 1956-vintage 2-D Cartesian “back-of-the-envelope” model described in reference 3 along with the atmosphere model. I updated this and reported those results in reference 4. Data groups are reported for the nominal 1200 kg/sq.m case, for “plus 500” (1700 kg/sq/m), and for “minus 500” (700 kg/sq.m), all on the nominal de-orbit trajectory. A plot of the salient results is given in Figure 3.


Figure 3 – Sensitivity Results

A data group is also reported for the “bigger de-orbit burn” trajectory, at the nominal 1200 kg/sq/m ballistic coefficient. That case was not included in the results plot, precisely because the steeper entry angle overcame the benefit of slower entry speed by so much, that surface impact occurred before the hypersonics were over. Surface impact occurred at a speed in the neighborhood of Mach 4.7, in this “typical” Mars atmosphere.

Reported Data and Methods

All data groups comprise spreadsheet images, a plot of velocity vs slant range, a plot of range and slant range vs altitude, a plot of deceleration gees vs slant range, and a plot of convective heating data vs slant range. These figures are all given at the end of this article.

For the heating data, the nose radius in the correlation was increased to a more realistic 50 m for a very large lander on the order of 7 m diameter. Tripling the heating data would probably “cover” the missing radiative heating effects, in the absence of better data.

The density scale height model was unchanged from that given in reference 3 (about 8.4 Km). This is not strictly accurate, but really doesn’t matter that much to calculated outcomes. This is because the scale height is just as non-constant from 0 to 25 Km altitudes, as it was for the 25-70 Km altitudes in reference 3. An average value for the lower altitude range (nearer 9.5 Km) is a bit different from that for the higher altitude range, but not by very much. The model is just about as “wrong” away from either average value. See Figure 4.


Figure 4 – Mars Density Scale Height Profile

Conclusions

1.It is critical that angle-below-horizontal be held to very low values in the neighborhood of 1.6 degrees, or less. One way to do this is to lower the circular orbit altitude. Another is the raise the periapsis of the entry trajectory above the surface (but not by too much).

2.For actual orbit conditions, a bigger deorbit burn reduces entry interface velocity, but steepens entry angle-below-horizontal. The angle effect is stronger, leading to surface impact before the craft can slow to Mach 3.

3.Vehicles in this class will likely come out of hypersonics at around 8 Km altitude, give or take a couple of Km, with only secondfs to go before surface impact, if not retarded at considerable gee.

4.These results are good enough to get “in the ballpark” for vehicle rough-out, but most definitely not good enough to support detail design.

References

1.G.W. Johnson, “Rough Correlation of Entry Ballistic Coefficient vs. Size for “Typical” Mars Landers”, article dated 7-25-12, posted to http://exrocketman.blogsapot.com.
2.G. W. Johnson, “Ballistic Entry From Low Mars Orbit”, article dated 8-5-12, posted to http://exrockretman.blogspot.com
3.“Atmospheric Environments for Entry, Descent, and Landing (EDL)”, C. G. Justus (NASA Marshall) and R. D. Braun (Georgia Tech), June, 2007.
4.G. W. Johnson, “Back of the Envelope Entry Model”, article dated 7-14-12, posted to http://exrocketman.blogspot.com.

Detailed Data

Detailed inputs and how they are used are given in Figure 5. The nominal case of 1200 kg/sq.m on the nominal de-orbit trajectory is described by Figures 6-10. The “plus 500” (1700 kg/sq.m) case on the nominal de-orbit trajectory is described by Figures 11-15. The “minus 500” (700 kg/sq.m) case on the nominal de-orbit trajectory is described by Figures 16-20. The “big de-orbit burn” case of the nominal 1200 kg/sq.m on the steeper trajectory is described by Figures 21-25.


Figure 5 – Detailed Inputs and Their Uses


Figure 6 – Spreadsheet Image for the Nominal Case (1200 kg/sq.m, 1.63 degrees)


Figure 7 – Nominal Case Velocity vs Slant Range


Figure 8 – Nominal Case Range and Slant Range vs Altitude


Figure 9 – Nominal Case Deceleration Gees vs Slant Range


Figure 10 – Nominal Case Heating vs Slant Range


Figure 11 – Spreadsheet Image for the “Plus 500” Case (1700 kg/sq.m, 1.63 degrees


Figure 12 – “Plus 500” Case Velocity vs Slant Range


Figure 13 – “Plus 500” Case Range and Slant Range vs Altitude


Figure 14 – “Plus 500” Case Deceleration Gees vs Slant Range


Figure 15 – “Plus 500” Case Heating vs Slant Range


Figure 16 – Spreadsheet Image for the “Minus 500” Case (700 kg/sq.m, 1.63 degrees)


Figure 17 – “Minus 500” Case Velocity vs Slant Range


Figure 18 – “Minus 500” Case Range and Slant Range vs Altitude


Figure 19 – “Minus 500” Case Deceleration Gees vs Slant Range


Figure 20 – “Minus 500” Case Heating vs Slant Range


Figure 21 – Spreadsheet Image for the “Big De-Orbit Burn” Case (1200 kg/sq.m, 6.4 degrees)


Figure 22 – “Big De-Orbit Burn” Case Velocity vs Slant Range


Figure 23 – “Big De-Orbit Burn” Case Range and Slant Range vs Altitude


Figure 24 – “Big De-Orbit Burn” Case Deceleration Gees vs Slant Range


Figure 25 – “Big De-Orbit Burn” Case Heating vs Slant Range