Because of repeated questions from knowledgeable readers, I took a more refined look at the scenario of chemical launch to eastward LEO at low inclination, using either an expendable two-stage to orbit design (TSTO), or an expendable single-stage-to-orbit design (SSTO). For this more refined look, I added delta-vee (dV) budgets for rendezvous and deorbit, I looked at a more representative orbital speed requirement, and I let the second stage of a TSTO shoulder a minority of the gravity loss (the split being arbitrary). The first stage shoulders all the drag loss. The SSTO shoulders all of both losses. See Figure 1.
Figure 1 – Revised dV Requirements That Are More Realistic
The 75-25 split on shouldering gravity losses is
arbitrary, but “in the ballpark”. I still picked 5% each for gravity and drag
losses, the basis being the kinetic
energy-equivalent surface circular orbit speed.
5% gravity loss would go with good kinematics off the launch pad, meaning 0.5 gee above gravity or better, or a thrust/weight of 1.5 or better at
launch. 5% drag loss would go with a
clean, slender shape, really meaning a length/diameter ratio of 6
or larger, with no steps in
diameter.
TSTO
Design Considerations
For the TSTO, what I
presumed was LOX-RP1 propulsion in the first stage, “compromise”-sized to improve the
ascent-averaged specific impulse (Isp),
such that the engine is just barely unseparated firing at sea
level, at 85% of max chamber pressure
Pc. I presumed LOX-LH2 propulsion in
the second stage, sized at an expansion
area ratio (A/A*) = 100, to limit engine
length.
Both the first and second stage engine technologies were
presumed to be modest technologies that do not push the state of the art (SOTA)
very hard, something that lowers
development costs that must be amortized over the launches to be made. Accordingly,
I presumed only a max Pc = 2500 psia,
and that whatever cycle it is has,
has a dumped bleed fraction of 2%.
The pressure turndown ratio (P-TDR) for throttling is only 2.5. The usual curved bell of 18-and-8-degree
profile is presumed, along with a throat
area discharge coefficient CD = 0.995.
Rather modest stage structural design technologies were also
presumed, such that both loaded-stage
inerts were 5% of stage ignition mass,
again to reduce development costs that must be amortized over the
launches to be made. 4% has been
demonstrated, but requires custom
alloys, even for expendables. The definitions are such that payload
fraction plus inert fraction plus propellant fraction sum to 1. The first stage payload is the fully-loaded
second stage, and the second stage
payload is a fixed 100 metric ton mass riding out in the open, atop the second stage.
All propulsion was initially sized for a thrust requirement
of 500,000 lb (226.76 metric tons-force,
2223.7 KN). For any ascent
engine, this was imposed at sea
level. For the TSTO second stage, this was imposed in vacuum. Performance was computed vs altitude, and those values averaged over the list of
altitudes in the altitude table.
That is not exactly correct for an “ascent-averaged
Isp”, because the vehicle does not spend
equal time at all these altitudes, but
it is well within the “ballpark”. I
compensated for any error by presuming an Isp about 2-5 s below what the sizing
calculation said. Dimensions and flow
rates depend upon sized thrust. Flow
rates and cross sectional areas scale in proportion to thrust, while linear dimensions scale in proportion
to the square root of thrust. Isp does
not scale.
The TSTO first stage sea level engine sizing to 500,000 lb
thrust is shown in Figure 2. The TSTO
second stage vacuum engine sizing to 500,000 lb thrust is shown in Figure
3.
Figure 2 – As-Sized TSTO First-Stage Engine Data, Un-Rescaled
Figure 3 – As-Sized TSTO Second-Stage Engine Data, Un-Rescaled
SSTO
Design Considerations
For the SSTO, I
looked at both LOX-LCH4 propulsion and LOX-LH2 propulsion. Such engines were “compromise”-sized for
better ascent-averaged Isp, just like
the first stage engines in the TSTO design. However,
the technology baseline presumed, pushes the SOTA very hard indeed: these designs presume a max Pc = 4000
psia, a cycle such that the dumped bleed
fraction BF = 0, and a more challenging
P-TDR = 3. (They would compare to the
SpaceX Raptor designs.)
I kept the same rather modest stage structural design
technology, with a stage inert fraction
of 5%. In this case, there is only one stage, and its 100 metric ton payload rides out in
the open, atop the stage, exactly the same as was presumed for the
TSTO.
The hydrogen-fueled version looked good enough to check the
effects of just modest-technology. That
would use the LOX-LH2 propellant ballistic models, but employ the same reduced Pc and
non-zero-BF that was used for the TSTO engine designs. The methane-fueled version had a low-enough
payload fraction to warrant skipping this look.
Figure 4 shows the un-rescaled methane engine results
for the edge-of-the-SOTA. Figure 5 shows
the un-rescaled hydrogen engine results for the edge-of-the-SOTA. Figure 6 shows an un-rescaled hydrogen
design of the same modest-technology parameters as were used in the TSTO
design.
Figure 4 – As-Sized SSTO Methane Engine, Edge-of-the-SOTA, Un-Rescaled
Figure 5 – As-Sized Hydrogen Engine, Edge-of-the-SOTA, Un-Rescaled
Figure 6 – As-Sized Hydrogen Engine, modest SOTA,
Un-Rescaled
Doing
More Detail
In my previous posting on this topic, “Launch to Low Earth Orbit: 1 Or 2 Stages?”, posted 3 March 2024, all I did was convert dV’s to mass ratios
MR, turn that into a list of mass
fractions, and then size a weight
statement from a fixed payload mass. I
used the stage ignition masses to size total thrust requirements. And that was it.
I have since added to the simple spreadsheets I used for
that analysis. If you look at the stage
overall thrust requirements and masses to be accelerated, you can choose a number of engines
appropriate for that stage, and thus
from that overall thrust requirement,
determine what those individual engine thrust ratings must be.
I created a little thrust-resize spreadsheet, which takes the as-sized engine data, and rescales them to the necessary thrust
rating. Areas and flow rates scale as
proportional to thrust, while dimensions
scale as proportional to the square root of thrust. What is important is the estimated overall dimensions
of an individual engine. Part of Figure
7 illustrates how these engine dimensions are scaled and created from the
estimated engine sizing data.
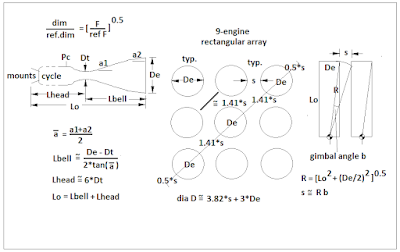
For only a 9-engine cluster,
I worked out how to use the engine dimensions and an assumed max gimbal
angle to estimate a clearance spacing between engine bells so that gimballing
one will avoid impacting an adjacent bell.
Adding this up along a diagonal of the 9-engine cluster provides an
estimate of the min stage diameter, as
is also shown in Figure 7. I used
15 degrees for the max gimbal angle, an
arbitrary choice.
Figure 7 – How Engine Dimensions Determine Stage Diameter
Once you have a min stage diameter estimate, you can begin to approximate the lengths of
the tanks, engine bays, and interstages. Those lead to a vehicle length/diameter ratio
estimate, from which to judge whether
the “slender” assumption justifying lower drag loss was justified. This is based on the same diameter for the
whole vehicle, to also qualify as
“clean”, for justifying the lower drag
loss assumption.
You can use an estimate of the engine’s operating r-ratio to
split total propellant mass into oxidizer and fuel masses, in each stage. You can use the standard specific gravity
values for those propellant materials to turn those oxidizer and fuel masses
into volumes (specific gravity is numerically equal to density in metric tons
per cubic meter). Dividing volume by
base area gets you a length of the tank that is an underestimate, since there are curved pressure dome
heads. Compensate by assuming an inter-tank
length of about a diameter.
First stage (or single stage) estimated engine length is the
length of the first stage engine bay (if there is one), but is part of the overall first stage length
regardless. If there is a second
stage, there is some sort of interstage
between it and the first stage, whose
length is the estimated overall length of a second stage engine. The length of the payload is arbitrarily
assumed to be 2 diameters.
The resulting augmented spreadsheet image for the TSTO
design is shown in Figure 8. The
leftmost block is the original mass and thrust sizing calculations. The rest is what I added to determine engine
counts and thrusts, and to use the
re-scaled engine dimensions to do the volumes and lengths. Images of the rescaled kerosene and hydrogen
engine spreadsheets were not included,
but are reflected in the dimensional data input at top right.
Figure 8 – Spreadsheet Image For TSTO Detail Sizing
A somewhat similar-looking spreadsheet was used for the SSTO
designs, starting with the LOX-LCH4
design looked at initially in the earlier posting. That produces the detail sizing spreadsheet
image of Figure 9, and the
associated engine re-scale spreadsheet image of Figure 10.
Figure 9 – Spreadsheet Image For SSTO Detail Sizing, Methane,
Edge-of-SOTA
Figure 10 – Spreadsheet Image For SSTO Engine Re-Scale, Methane,
Edge-of-SOTA
The reader should be aware of one disconnect here: I picked 15 engines, not 9!
The stage diameter estimate is wrong:
it is too small! That lowers the
vehicle L/D ratio even further, from the
too-low value already obtained. For this
design, the drag dV loss to cover should
have been more than the 5% used in the velocity requirements analysis shown in Figure
1 above.
So as it turns out,
the recommendation in the earlier posting to use the LOX-LCH4 propellant
combination for the SSTO design has been shown to be wrong! This also shows up in the 2.1% payload
fraction and the enormous 4850 metric ton ignition mass, given in Figure 9 above.
Accordingly, I did
another edge-of-SOTA design for the SSTO,
this time using LOX-LH2 propulsion.
The image of the detail sizing spreadsheet is given in Figure 11. The engine dimension re-scaling is shown in Figure
12. This one actually uses 9
engines, so the diameter is
“right”, and so is the L/D.
Figure 11 -- Spreadsheet Image For SSTO Detail Sizing, Hydrogen,
Edge-of-SOTA
Figure 12 -- Spreadsheet Image For SSTO Engine
Re-Scale, Hydrogen, Edge-of-SOTA
Comparing the payload fractions and ignition masses between Figures
8 and 11, 7.5% and 1401 tons TSTO vs
7.5% and 1325 tons SSTO, we see pretty
much equivalent performance between the TSTO using LOX-RP1 and LOX-LH2 both at
modest engine SOTA, and the SSTO using
all-LOX-LH2, but at the edge of the
engine SOTA. Clearly the higher average
ascent Isp of the hydrogen vs the methane made a huge difference for the
SSTO, more than I initially expected
to see!
That brings up determining the effects of pushing the engine
SOTA so hard with the SSTO engines. To
determine that, I used the modest SOTA
hydrogen ascent engine data of Figure 6 above, to create yet another SSTO design
sizing, by these same methods. The detail sizing spreadsheet image is given
in Figure 13, with the engine
re-scale data in Figure 14.
Figure 13 -- Spreadsheet Image For SSTO Detail Sizing, Hydrogen,
Modest SOTA
Figure 14 -- Spreadsheet Image For SSTO Engine
Re-Scale, Hydrogen, Modest SOTA
This one is not that much reduced in payload capability
(6.7% vs 7.5% for the Edge-of-SOTA SSTO and the TSTO). It increased its launch mass a little, being 1487 metric tons, vs 1325 for the edge-of-SOTA SSTO and 1401
for the TSTO. Yet they are all 3 in the
same basic class of vehicle sizes. I did
select 9 engines, so the diameter is
valid, and the L/D is “good”. There is no reason the more modest
hydrogen engine technology might not serve,
and serve well.
Results
and Conclusions
Sketched images for the TSTO with
modest-technology kerosene and hydrogen propulsion, the SSTO with SOTA methane propulsion, the SSTO with SOTA hydrogen propulsion, and the SSTO with modest-technology hydrogen
propulsion, are given in Figures 15
through 18 below, respectively.
As the table above indicates, it is ascent-averaged Isp that is the
critical factor here with the SSTO.
The big gulf between the methane and hydrogen/SOTA ascent-averaged Isp’s
corresponds to the big gulf between the payload fractions and the ignition masses. The small gap between the hydrogen/modest and
hydrogen/SOTA Isp’s corresponds to the small gap between payload fractions and
ignition masses.
Changing the propellant combination had a huge effect on
ascent-averaged Isp and the resulting sized designs. Changing how hard the hydrogen engine
technology pushes the SOTA did not have a large effect, only a smaller one. The sized design reflects exactly that. See also Figure 19 below.
Before I ran this more detailed design study, I thought that pushing the SOTA vs a modest
technology would have more of an effect than it actually did. Now we see:
the propellant combination has the far stronger effect. Go ahead and use the more modest engine
technology. That will not stop you from
doing rather well as an SSTO, as long as
you use LOX-LH2.
The hydrogen upper stage TSTO with modest engine technology
is only a little better in terms of payload fraction than the hydrogen SSTO
with modest engine technology. But, it does offer an easier path to partial
reusability, by substituting a larger
lower stage with the ability to fly back and land. That is something to consider.
The “compromise” expansion sizing approach for ascent
engines is very important, as that is
how one achieves ascent-averaged Isp values higher than an ordinary sea level
design.
That sort of “ascent-averaged Isp is dominant” outcome for
the SSTO makes me wonder if we could do better than a kerosene first stage for
the TSTO. While beyond scope here, I will look at that in a future update or
posting. The candidates are methane and
hydrogen, of course. These will be restricted to “modest engine
technology”. The same methods will be
used, as were used here.
I do expect that one or both will significantly exceed what
we can do with a modest-technology hydrogen SSTO. The problem will be the same volume issues
that afflicted the SOTA-technology methane SSTO. But we will not know, until we try.
Figure 15 – Image of Detailed Results for TSTO, Modest Kerosene and Hydrogen
Figure 16 – Image of Detailed Results for SSTO, SOTA Methane
Figure 17 – Image of Detailed Results for SSTO, SOTA Hydrogen
Figure 18 – Image of Detailed Results for SSTO, Modest Hydrogen
Figure 19 – Plots Showing Relative Effect of Engine
Technology Level and Propellant Combination
-----
Update 3-12-2024:
I carried out the plan outlined at the end of the article
above, to investigate two
higher-performing propellants in the TSTO.
That required sizing a LOX-LCH4 engine of modest technology to be an
ascent engine in the first stage. I
already had a LOX-LH2 ascent engine sized,
of modest technology,
investigated for the SSTO. These
were both resized to fit a 9 engine cluster of the necessary thrust, just as in the studies done in the article
above, with the updated vehicle sizing.
For these changes to the TSTO, I did not change its second stage at
all. It was, and still is,
powered by two small LOX-LH2 engines of modest technology, sized as vacuum engines with A/A* = 100, just as before. The resized modest-technology methane ascent
engine is illustrated in Figure 20 below. The sized TSTO vehicle with that set of modest
technology methane engines in its first stage is depicted in Figures 21 and
22 below. The sized TSTO vehicle with a set of modest technology hydrogen
engines in its first stage is depicted in Figures 23 and 24 below.
I did not see much difference between the kerosene and
methane first stage TSTO vehicles in terms of payload fraction, but the ignition weight did reduce somewhat, going to methane. A part of this is the reduced thrust
requirement reducing engine lengths, in
a vehicle whose length and diameter are primarily sensitive to engine
dimensions and number. With a hydrogen
first stage, the payload fraction
increased noticeably, and the launch
weight decreased significantly further.
I had not reduced the ascent-average Isp of the modest
technology hydrogen ascent engines by 2-5 s when I did the hydrogen TSTO in the
article above, inputting 447 s to the
vehicle sizing. Here, I did,
inputting 445 s Isp to the vehicle sizing. I ignored this small difference
making the comparison plots of trends with the two vehicles, which is Figure 25 below. The main takeaway is the lower slopes of the
trends with the TSTO, compared to the
steep slopes of the trends for the SSTO.
There is a good, simple reason for that: the TSTO second stage is vacuum hydrogen-powered, and shoulders the majority of the dV requirement imposed on the vehicle. That makes the first stage mass ratios rather small in comparison, where the added benefit of higher first-stage Isp is “diluted” by the constant-second stage effects. In contrast, the SSTO has to get all the dV requirement out of its single stage. The benefits of the higher Isp are entirely undiluted by anything, hence the effects are large, and the trend slopes are steep.
Figure 20 – Sized Methane Ascent Engine of Modest Technology
Figure 21 – Vehicle Sizing Data for Modest-Technology
Methane Engines in the First Stage
Figure 22 – Vehicle Sketch for Modest-Technology Methane
Engines in the First Stage
Figure 23 – Vehicle Sizing Data for Modest-Technology
Hydrogen Engines in the First Stage
Figure 24 – Vehicle Sketch for Modest-Technology Hydrogen
Engines in the First Stage
Figure 25 – Comparison Plots of Trends, With All Vehicles
Conclusions
The results here are for all-expendable vehicle
sizings. The conclusions apply to the
same, with exceptions for re-usability as
stated in notes 7 and 8.
#1. If you design a TSTO expendable “from scratch” for
delivering large payloads to LEO, always
use a LOX-LH2 engine designed for vacuum operation to power the second
stage.
#2. If you design a TSTO expendable “from scratch” for
delivering large payloads to LEO, it
does not matter very much which of the 3 propellant combinations you use for
powering the first stage. The trends
favor LOX-LH2, but these trends are weak
(low slope). LOX-RP1 and LOX-CH4 also
serve well.
#3. Whether you design “from scratch” a TSTO expendable or
an SSTO expendable for delivering large payloads to LEO, use “ascent engines” with their expansion ratio
designed as an ascent compromise: just
barely unseparated, at around 85% max Pc,
at sea level. Engines designed in this way will have a
higher ascent-averaged Isp than traditional sea level engine designs, which are generally perfectly expanded to sea
level pressure at max Pc. And the actual
flight configurations are testable at
sea level in the open-air nozzle mode,
which helps to greatly lower development costs that must be
amortized, and to greatly lower
development risks.
#4. If you design “from scratch” an SSTO expendable for
delivering large payloads to LEO, go for
the LOX-LH2 propulsion. Because of the
steep trends, these designs are critically-sensitive
to ascent-averaged Isp above all other considerations. Only LOX-LH2 provides high enough Isp.
#5. Neither type of vehicle is extremely-sensitive to how
hard the engine technology pushes the SOTA,
because the Isp difference is not all that large between high-SOTA and
rather modest technology, something true
for all 3 propellant combinations. With
the more modest technology, development
risks and efforts are lower, leading to
lower development costs to be amortized.
#6. I did not evaluate the impact of stage structural
design technology! I got good results
from the best of the designs at a rather modest stage inert mass fraction
assumption: 5% inert in every loaded
stage. 4% has been demonstrated, but I deliberately chose not to push those
limits! The less demanding structural
design lowers development effort levels and development risks, thus lowering the development costs to be
amortized.
#7. The TSTO offers a fairly easy path to partial
re-usability, by enlarging the first
stage design to enable its flyback,
entry, and recovery. This is primarily enabled by the relatively-low
(only supersonic) speeds at entry, in
turn imposed by the relatively low staging speed, which also lowers the burn-back dV
requirement.
#8. The SSTO does not offer an easy path to
re-usability, because the entry speeds
are orbital-class hypersonic, and the
stage simply does not have the inert fraction to permit the design changes to
make it into a survivable entry vehicle at all,
much less to land. The “proof” is
in the negative: if this were not true
as stated, it would have already been
done, routinely, along with first stage recoveries.
Final
remarks
Do not take these “designs” as ready-to-build! While the engine ballistics and performance
estimates are rather good, the weight
statements are less so, and the
dimensional estimates are only “ballpark”.
It is the trends that should be used to support real design
candidate screening and selections. Some
of that screening I have done for you,
in this article.
To address questions from knowledgeable readers, I made the dV requirements more
representative of vehicles that can get to orbit and rendezvous with a
destination, plus a deorbit capability
for proper disposal. But, there are a lot of things that I did not
address.
I did not address propellant ullage / engine relight
issues, and I did not address the
unrecoverable propellant fractions that are inherent with any type of tank
design. Further, I did not address the actual end dome
shapes or designs of the liquid propellant tanks, or the possibility of a common dome
design, which can be done with some
propellant combinations, but by no means
all of them.
These are not only “from scratch” vehicle ballpark design
sizings, they are also “from scratch”
paper engine design sizings, a
start-point only for a real engine design and development effort. I made absolutely no attempt in this
work, to use any pre-existing engine
designs of any kind at all!
My work here can be re-scaled to other delivered payload
masses (the 100 metric tons that I used here was an arbitrary number), so that the trends I uncovered can help guide
real concept selection and real design efforts for other-size projects done by
others. If a pre-existing engine of the
right propellant combination fits your design project, so much the better! Any development costs you can avoid are one
less thing to amortize over the life of the product.