The first few sections here are reprised (with edits) from
“Just Mooning Around”,
posted 7-14-19.
This year has been the 50th anniversary of the
first man on the moon. That was the
culmination of the space race between the US and Soviet Russia. That accomplishment was a whole lot more
about “flags and footprints” and experimental flight test, than it was about science or real exploration.
This article builds upon some earlier articles posted upon
this site. It presents the latest
version of my Mars mission outline plan,
with an enlarged manned transport,
and the latest sizing of 1-stage 2-way reusable chemical landers. These earlier articles are as follows:
Date Title
14 July 2019 Just
Mooning Around
28 May 2016 Mars
Mission Outline 2016
13 December
2013 Mars Mission Study 2013
31 August 2013 Reusable
Chemical Mars Landing Boats Are Feasible
Why We Should Go Back (And Farther Still)
Is there anything worthwhile to accomplish out there? Yes,
definitely!
In the longer term,
there are those future off-world settlements and the associated future
economies. I cannot tell you the details
of how this might benefit us, because it
has yet to be done. But it has always
proven beneficial in prior centuries here on Earth.
In the shorter term,
there are the possibilities of space resource businesses, and of planetary protection against
rogue asteroid and comet impacts. That
second item is the most important of all:
there is simply no better reason for continuing both unmanned and manned
space programs than finding ways to protect the folks back home!
It’s not about winning some race, and it’s not so very much about doing pure
science just for the sake of knowledge.
It’s about real exploration of the unknown, something hard-wired into humans. In centuries past, this was exploration of the unknown parts of
the Earth. Now it is about space and the
deep ocean floor. This article is
concerned with the real exploration of space.
“Exploration” is a really an emotionally-loaded code word, something most people do not think about. What it truly means is you go there to
find out “what all is there” (resources,
including those you don’t at first recognize), and “where exactly it is” (how hard to obtain, as well as how much is there). Then you have to stay a while to figure
out how to use what you found, in
order to cope with living in the local environment. All of that is part of “real exploration”.
Unless you do that correctly, there is no real possibility of future
settlements and the associated future economies, or any of the benefits that would ultimately
derive therefrom! There is no way to
accomplish much of anything else, except
just the “flags and footprints” act of going there and returning (which is the
bulk of what Apollo itself really accomplished at the moon).
Those who “get there first” do tend to do a little better in
the long run, in terms of those benefits, provided that they do it “right” when they go. That is one crucial lesson from history.
My Suggestions for the Near Term
Establish a continuous human presence on the moon, the first item. Start small and expand it slowly over time. Do
the lunar “exploration” thing right,
this time.
Send humans to Mars as the fulfillment of a dream centuries
old, probably the second item. When we go,
do the “exploration” thing right,
from the very first landing. Further, it starts long before the first item (going
to the moon) is “done” in any sense of that word.
But, any vehicle
capable of taking crews to Mars can also take a crew to near-Earth asteroids
and comets. Visit those asteroids and
comets and properly explore them, in
order to learn how to defend against their impacting Earth, as well as “ground truth” for how to really do
space mining.
That’s the third item,
but it is just as easily done,
and at least as important, as
going to Mars.
Maybe we do them at pretty
much the same time.
Ethically and Responsibly Addressing Known Risks For Spaceflight
We are ethically-bound to address the known risks of manned
spaceflight as best we can. There is
a whole long list of safety risks associated with any sort of manned spaceflight. Three come to mind as the most truly credible
risks: (1) reliability of, and escape from, spacecraft and booster rockets, (2) microgravity diseases, and (3) exposure to space radiation.
The first one has cost us three American crews totaling 17
people dead (Apollo 1, shuttle Challenger, and shuttle Columbia). Each caused a year-or-more stand-down, and very expensive investigations, plus very expensive changes.
The two shuttle losses were ultimately caused by bad
management decisions valuing cost or schedule above safety. Apollo 1 was about a really-poor basic
management attitude (“good enough for government work”) combined with technical
ignorance, because we had never done
this sort of thing before.
Those outcomes and their actual causes are why I claim
“there is nothing as expensive as a dead crew,
especially one dead from a bad management decision”. Bear in mind that those expenses are both
economic and political (which includes public opinion as well as DC politics).
Making spaceflight more safe, from a reliability and escape standpoint, is now also something we already know how to
address! This takes careful design
allowing for failure modes, redundant
systems, and copious verification
testing. Mitigation efforts will
never be perfect, but they can be quite
good. Ethics requires that you treat this as a required constraint
upon your designs.
It means you always provide “a way out” for your crew
at every step of the mission. It
really is as simple (and as hard to do) as that! This very seriously constrains your
overall mission architecture, as well as
your detailed space vehicle designs.
The other two have been long studied in low Earth
orbit, where microgravity exposure is
inherent in everything we have done there,
and radiation exposure is somewhat more than on Earth’s surface, but less than outside the Van Allen radiation
belts (and far less than inside the belts themselves).
Microgravity
Diseases
Microgravity has proven to affect the human body in a
variety of expected, and unexpected,
ways.
The longer one is exposed, the
worse the various diseases become. Beyond
the bone decalcification and muscle-weakening that we have long expected, there are also degradations of the heart and
circulatory system, degradation of
vision from eye geometry changes due to the fluid pressure redistribution, immune system degradations that we have yet
to understand, and most recently genetic
changes whose meanings are still a total mystery. No doubt more will be discovered, as that has been the trend.
The longer exposed,
the longer it takes to recover upon returning home, with full recovery actually still in doubt
for some of the effects, despite
diet, drugs, and exercise. The practical time limit
seems to be only a bit more than a year. For that very reason, usual practices on the International Space
Station (ISS) call for 6 months to a year’s exposure at most, with 6 months the preferred limit.
We do know that something near one full Earth gravity (one
“gee”) is therapeutic, precisely because
that is what we evolved in. So, until we know better, any artificial spin gravity schemes
need to supply very near one gee,
in order to obtain the full Earthly benefits that we already know will work.
Destinations outside of Earth-moon space are very much
further away than the moon: one-way
travel times range from near 6 months to multiple years. This is pretty much outside the preferred limit
of microgravity exposure that we have already established on ISS.
Mars is 6-to-9 months away one-way, and we do not know how therapeutic its
lower gravity (38%) really is for the rigors of the return voyage. Other destinations are further away
still, and all those we can actually
land upon, are even lower gravity
than Mars. That situation says
quite clearly that we need to provide artificial gravity (no matter how
inconvenient that might otherwise be !!!!) at something near one gee
(until we actually know better !!) during these one-way transits
to-and-from, in order to best
preserve the health of the crews.
Ethically, you simply
cannot argue with that conclusion, no
matter how inconvenient for design purposes, or for total mission cost purposes. That is the only “box on thinking”
applied here.
Supplying
Artificial Gravity
There is as yet no such thing as “Star Trek”-type
artificial gravity. The only physics we
have to serve that purpose is “centrifugal force”. You must spin the vehicle, to generate “centrifugal force” as an
equivalent to gravity. If the spin rate
is low, then Coriolis forces (something
everyone has experienced on a merry-go-round) become less important, and so fewer folks can tell the difference
between this and real gravity, and
there are fewer problems with disrupting the balance organs in the ear.
The physics of spin say that the acceleration you feel is
proportional to the radius of spin and to the square of the spin rate. The actual physics equation says
a = R w2 where a is the acceleration, R the spin radius, and w the spin rate
Another form expressed in gees, and not absolute acceleration units, is
gees = 1.00
* [(R, m) / (55.89 m)] [(N, rpm) / (4 rpm)]2
Earthly experience with spin rates says that normal
untrained and unacclimatized people can tolerate 3 to 4 rpm immediately, and for long-term exposures, without getting motion sick. People extensively trained might (or might
not) tolerate higher spin rates in the 8-12 rpm class, without getting motion sick from long
exposures. Still-higher spin rates (16+
rpm) induce blood pressure gradients head-to-toe in a standing individual, that are just unacceptable for long term
exposures. Stand up, and you faint.
3-dimensional objects typically have 3 axes. About these axes these objects have properties
called “mass moment of inertia” that relates to spin dynamics. Usually,
higher moment of inertia correlates with a larger dimension along some
axis perpendicular to the actual spin axis.
These are typically proportional to mass, but proportional to the square of its
distance from the center of gravity.
There are two (and only two !!) stable spin modes for most
objects: about the axis for highest
moment of inertia (longest dimension),
and about the axis for lowest moment of inertia (shortest dimension). The first case is exemplified by a baton
twirler’s spinning baton, and the second
case is exemplified by a spinning bullet or artillery shell. There are no other stable modes of
spin. See Figure 1.
Figure 1 – Modes of Spin
Clearly, building a
“spinning rifle bullet” 112 m in diameter at 4 rpm for one full gee at its
outer girth is not so very feasible:
this is just too big to afford at this time in history. But spinning a smaller-diameter “something”
that is 112 m long, end-over-end at 4
rpm, for 1 gee at each end, would indeed be a feasible thing to attempt! That says select the baton-spin mode
for practical designs.
We already know a lot about the transient dynamics of
spinning rigid objects, something
important for spin-up and spin-down, as
well as for applying any thrust while spinning.
There would be no fundamental engineering development work to design a
long, narrow spacecraft that spins
end-over-end for artificial gravity.
There would only be proving-out the specific design in tests before we
use it.
The most-often-proposed alternative is a cable-connected
structure, because it is conceptually
easy to reel-out long cables between two small objects. Cable-connected transient dynamics for
spin-up and spin-down, and especially
for applying thrust while spinning, are
incredibly complex and still not very well-known. “You cannot push on a string”, that is the complication! So there is a huge fundamental engineering
development effort needed, beyond
just proving-out the actual design to be used.
What this really says is that the preferred near-term spacecraft
design is a long and rigid, more-or-less
cylindrical shape, to be spun
end-over-end, baton-style. This will generate varying artificial gee
from a maximum near the ends, to zero at
the spin center.
We know that microgravity vs gravity has no impact while
prone sleeping, or else Earthly bed rest
studies would not be a decent surrogate for some of the in-space microgravity
effects. That means you can put the
sleeping quarters in the low gravity section of the spacecraft near the spin
center, and just put the daily
workstations in the full-gravity sections of the spacecraft near the ends. See Figure 2.
Figure 2 – Why Selecting Baton Spin Mode Is Wisest Choice
Radiation
Hazards
There are basically three radiation hazards to worry
about: galactic cosmic rays (GCR), solar flare events (SFE), and the Van Allen radiation belts about the
Earth (or similar belts around some of the outer planets). All three hazards are atomic or subatomic particles, just at different speeds and quantities. The threats they pose are location-dependent.
GCR is a very slow drizzle of really-high-speed particles, moving at a large fraction of the speed of
light. Particles that energetic are very
difficult to shield against, because
they penetrate deeply into shielding material,
and quite often create “secondary showers” of other harmful radiation
when they strike the atoms in the shield material. If the shielding atoms are low atomic
weight, the secondary shower effect is
greatly reduced.
GCR comes from outside the solar system. Its quantity is affected by the solar
wind, in turn affected by the sun’s
sunspot cycle, which is about 11 years
long. The solar wind is stronger when
sunspots are active, making GCR lower in
the vicinity of the Earth-moon system at that time.
From NASA’s radiation effects website (ref. 1), I obtained these values that apply in the general
vicinity of the Earth-moon system. GCR
maximizes at about 60 REM per year when the sun is quiet, and minimizes at about 24 REM per year, when sunspots are most active. To “calibrate” the effects of what may be
unfamiliar units of radiation, the
natural Earthly background radiation is about 0.3 REM per year (and up to 10
times higher in some locations), and
a lethal dose would be 300 to 500 REM accumulated in a “short time”, meaning hours to a week or so. (Just for information, 1 Sievert is 100 REM.)
The NASA astronaut exposure standards are set at about twice
the levels allowed for Earthly nuclear workers.
Those NASA standards are no more than 50 REM per year, no more than 25 REM in any one month, and a career limit that varies with age and
gender, but maxes-out at no more than
400 REM accumulated over an entire career.
These career limits are predicated upon a single-handful percentage
increase in the likelihood of late-in-life cancer.
Clearly, with a
very modest shielding effect (to reduce worst-case 60 REM to an acceptable 50
REM annual), GCR is not the “killer” it
is often portrayed to be.
SFE (solar flare events) are different. They are much lower-speed particles, much easier to shield, but there is an incredibly-huge flood of
them, when these events happen. They come in very-directional bursts
from the sun, at rather erratic
intervals. There are usually
more of them during times of active sunspots,
but they can indeed happen when the sun is quiet. They come at irregular intervals measured in durations
of “several months apart”.
The intensity of a burst can vary wildly from only tens
of REM received over a few hours, to
tens of thousands of REM received over a few hours. The median dose would be multiple
thousands of REM over a few hours. Obviously, for unshielded persons, the great bulk of events like this (those
over about 300-500 REM) would be fatal doses,
and it is an ugly, irreversible, and miserable death. There was a massively-fatal-level event in
1972 between the last two Apollo missions to the moon, and a low-intensity (non-fatal) event during
one Apollo mission to the moon.
We had chosen to ignore this SFE threat during Apollo
because the short duration of the missions (at most 2 weeks) was small, compared to the typical interval (several
months) between events. But, had a large event hit during an Apollo
mission, the crew would have died in
space in a matter of hours. As it
turns out, this actual record shows that
Apollo’s “ignoring-the-risk-as-low-probability”-assumption was not a
good assumption to make! That’s 20-20
hindsight, but it is still a crucial
lesson to learn!
For an extended or permanent return to the moon, or going elsewhere, radiation shielding is obviously imperative! On Earth,
we are protected from these SFE’s (and the GCR) by both the Earth’s
magnetic field and its atmosphere. These
are a very real threat anywhere outside the Earth’s magnetic field! In low Earth orbit, we are protected only by the magnetic
field, and the background exposure there
is higher than down on Earth, but still much
less than beyond the magnetic field.
The Van Allen belts are concentrated regions of these same radiation
particles trapped in the Earth’s magnetic field. The intensity is lethal on a scale of days-to-weeks, but tolerable on a scale of hours-to-a-day-or-so. The inner boundary is not sharp, but this is generally considered to become a
problem at about 900 miles orbit altitude,
and extending many tens of thousands of miles out from the Earth.
The exception is the “South Atlantic Anomaly”, where the inner side of the Van Allen belt
dips down locally to low Earth orbit altitude (100-300 miles). Satellites and spacecraft in high-inclination
orbits inherently pass through the South Atlantic Anomaly every several orbits. The ISS does indeed encounter this threat, it being short “flashes” of exposure that accumulate
over time, but these still fall well within
the astronaut exposure standards (no more than 50 REM annually, no more than 25 REM in any one month). Their main effect is accumulation toward career
limits.
Spacecraft traveling to the moon or elsewhere must transit
the Van Allen belts. Because of the
potential for lethal exposure if you linger within them, such transits must be made quickly! Apollo did this correctly, transiting within only several hours. Given the state of today’s electric
propulsion technology, this rules out
using electric propulsion for people to leave Earth orbit for the moon or
elsewhere, because the spiral-out time
is measured in multiple months. That
would quickly accumulate to a lethal exposure,
even with some shielding.
Passive
Shielding
The same NASA radiation site has data regarding the
shielding effects of typically-considered materials. Those are hydrogen, water,
and aluminum. Mass of shielding
above a unit exposed area turns out to be the “correlating variable”, and 15-20 g/cm2 seems to be enough
to generally address the worst SFE.
Hydrogen has the lowest density, requiring the thickest layering, but also has the least secondary shower potential, when used against GCR. 211 to 282 cm of liquid hydrogen
suffices.
15-20 cm of water is 15-20 gm/cm2, same shielding effect as a really thick layer
of hydrogen. Water molecules are still light
enough not to have much secondary shower risk.
Aluminum would be the thinnest layer, but with the greater secondary shower
effect. However, of the practical metals, its atoms are the lightest, and this secondary shower effect is deemed
tolerable with it. 6-8 cm thick aluminum
plate would be required. That is
quite out-of-line with current spacecraft hull design practices: something nearer a millimeter.
Other materials based on polymers, and even most rocket propellants, are light-enough atoms to be effective shielding
with a low secondary shower risk, yet
with densities roughly in the same ballpark as water, for a thinner layer thickness. So,
any of these could be practical shielding materials!
Because weight is critical,
what you have to do is not simply add shielding weight to your
design, but instead rearrange the
distribution of masses you already otherwise need, so that they can also serve as radiation
shielding. You will need meteoroid
shielding and thermal insulation, and
any manned craft will have water and wastewater on board, as part of the life support system. All spacecraft will need propellant for the
next (and subsequent) burns. You
use a combination of these, acting
together.
The real suggestion here is to use water, wastewater,
and next-burn propellant tankage as shadow shields, in addition to the meteoroid protection and
thermal insulation materials that the manned modules require anyway. It doesn’t take much of this at all to cut
the worst-case 60 REM/year GCR to under 50 REM/year. It takes only a little more to cut worst-case
SFE to safe short-term exposure levels.
If you cannot protect the whole manned interior, then the flight control station becomes first
priority, so that maneuvers can be
flown, regardless of the solar weather. Second priority would be the sleeping quarters, to reduce round-the-clock GCR exposure
further. These seriously constrain
spacecraft design.
See
Figure 3 for one possible way to do this, in an orbit-to-orbit transport design concept. This would also be a baton-spin vehicle
for artificial gravity during the long transit. Plus, the
habitation (“hab”) design requires a lot of interior space for the mental
health of the crew, something else we
know is critical. Somewhere
between 100 and 200 cubic meters per person is needed as a minimum, and at least some of it must be
reconfigurable as desired by the crew.
Spin-up is likely by electrically-powered flywheels in the
center module. The vehicle is spun-up
after departure, and de-spun before
arrival. If a mid-course correction is
needed, the vehicle could be de-spun for
that, and spun back up for remainder of
the transit.
Note in the figure how the arrival propellant and the water
and wastewater tankage has been arranged around the manned core to provide
extra shadow shielding, for really
effective radiation protection. The
manned core modules are presumed insulated by polymeric layers that also serve
as meteor shielding (while adding to the radiation protection, without being driven by that issue). The pressure shell on the inside of this
insulation should be unobstructed by mounted equipment, so that easy and rapid access for patching of
holes is possible. There is not time to move stuff when a compartment is
depressurizing! Ethics!
At departure, the
vehicle can be propelled by a different propellant and engine choice, since departure is a short event. The arrival propellant is likely a storable
to prevent evaporation losses. Storable
return propellant tankage sets can be sent ahead unmanned, for docking in orbit at the destination.
There is an emergency return capsule (actually two capsules)
mounted at the center module, each one enough
for the entire crew. (“Bailout” at Mars
presumes a rescue capability already exists there, so we need redundant engines instead.) Emergency
bailout, upon a failed burn for returning
to Earth orbit, is the main function of
this capsule. Routinely, it could return a crew to Earth from the
spaceship, once it is parked safely in Earth
orbit.
This kind of orbit-to-orbit transport design could serve to
take men to Mars or to the near-Earth asteroids and comets. For Mars,
the lander craft could be sent ahead unmanned to Mars orbit, and none are needed to visit asteroids. But you cannot send return propellant ahead
on an asteroid mission.
By refueling and re-supplying in Earth orbit, such a manned hab design could easily be used
for multiple missions, once built. Care must be taken in its design and material
selection to support many thousands of cycles of use. Thus the craft could safely serve for a
century or more, updated with better
propellants and engines as the years go by.
There I went and wrote a basic “how-to” document for
practical and ethical interplanetary spaceship design!

Figure 3 – Using Otherwise-Required Materials To Also Serve
As Radiation Shielding
These first few sections so far have been reprised (with
edits) from “Just Mooning Around”,
posted 7-14-19. Everything that
follows is new.
Mars Mission Outline 2019: Overall
The new version uses a larger orbit-to-orbit transport, and recovers the solar-electric tugs that
preposition unmanned assets at Mars for the manned mission (2016 did not). It uses similar (but larger) landers as the
2016 version, and it still jettisons the
Earth departure stage without recovery.
That last could be addressed by fitting the departure stage with a
second propulsion system, possibly
electric, and putting it into a 2-year-period
orbit after stage-off. Then it could be
captured into Earth orbit for reuse. That
recovery possibility is beyond scope here in the 2019 version. Consider it to be a “future update”.
Main point here: if
one does spin gravity in a baton-spin mode,
the resulting transit vehicle is ill-adapted for a direct entry at
Mars, or a direct entry at Earth. Such a design is far better-adapted as an
orbit-to-orbit transport, with any Mars
lander function relegated to a separate vehicle, sent separately. Long-life reusability also points toward an
orbit-to-orbit transport design, free of
entry heat shield requirements. It
means we base our exploration forays onto the surface of Mars from low Mars
orbit.
The resulting mission architecture requires that both
the landers and the Earth return propellant get sent ahead unmanned to
parking orbit about Mars, with the
manned orbit-to-orbit transport arriving afterward, and rendezvousing in Mars orbit with those
items. This powerful concept is
not unlike the Lunar Orbit Rendezvous architecture that made it possible to
mount each Apollo landing mission with only one Saturn 5 booster. See Figure 4 for the overall mission architecture.
Figure 4 – Overall Mars Mission Architecture Requiring Mars
Orbit Rendezvous
The landers themselves are envisioned as one-stage
reusable articles that make multiple flights, based out of low Mars orbit. Sending 3 landers ahead with their propellant
supply allows one lander to make a landing with only part of the human crew, with a second lander in reserve as a rescue
craft. Thus, there is a “way out” even during the
landings, unlike with Apollo!
Because of storability concerns, the wisest choice is that the lander
propellant and engine design be the same as the transport propellant and
engine design. This maximizes the
interchangeability of engine hardware and propellant supplies, in the event that there are mishaps from
which to recover, without aid from
Earth. It also simplifies the overall
design and hardware development and prove-out.
The presence of a third lander allows one lander to become
unserviceable, while still
maintaining the reserve rescue lander capability, without which landings so far from Earth
become too risky to ethically attempt.
This is shown in Figure
5, including the velocity
requirements for the lander design.
The initially-sized version of the lander design concept was
used in the 2016 posting, and came from
one of the options explored in another posting titled “Reusable Chemical Mars
Landing Boats Are Feasible”, dated 31
August 2013. These landers are resized
somewhat for this posting.
Figure 5 – Surface Landing Forays Based Out Of Low Mars
Orbit
Note that for a rescue possibility to exist, some of the crew must stay in the transport
in low Mars orbit, while others descend
to the surface in a lander.
Because we do not know how therapeutic Mars’s 0.38 gee gravity might be
for the surface crew, I suggest we spin
the transport for artificial gravity while it is in orbit, de-spinning for lander departures and
arrivals. Thus everybody stays fully
healthy no matter what, while we
alternate crews on the surface.
Now, overall, it is worst-case 9 months to and from
Mars, and in any case, 13 months at Mars waiting for the orbital
“window” to open for the voyage home. That
last is simply inherent from the choice of min-energy Hohmann transfer orbits. That leaves a long time for the crew to
explore on Mars. That plus the
possibility that the initial landing site might not prove to be desirable, makes it wise to plan for multiple
landings, at possibly-multiple
sites.
Basing exploration forays from low Mars orbit is
what makes multiple landings at multiple sites possible at all! No other mission architecture can
provide this capability.
It is that orbit-based architecture allowing for multiple
landings which lets us alternate roles for the crew, so that all of them get to spend time on
the surface of Mars (unlike what was possible with Apollo). With a mission crew of 6, that means we could send down alternating
crews of 3 in the lander, while the
other 3 do science from orbit and provide the critical watchdog rescue
capability with the other two landers (two for the reliability of
redundancy). It is already known that
odd numbered crews fare better in hazardous situations, there being no possibility of the stalemate
of ties, in decision-making.
Given the existence of the rescue capability from low Mars
orbit, we can address lander reliability
in two ways, thus increasing the odds of
success, and also the odds of still saving
the lander crew, if things go seriously
wrong. (We are ethically bound to do this!) First,
the lander must use redundant engines,
so that if one fails, the
remaining engine (or engines) can still perform the mission.
Second,
the crew piloting cabin could be rigged as an abort-to-surface (or
abort-to-orbit) capsule, in the event
that too many redundant engines fail, or
that there is some overall catastrophic failure of the lander.
The minimum number of landings is two, one for each half of the crew. Allowing some time for
reconnaissance-from-orbit prior to the first attempt, and for preparations for returning to
earth, we can plan on 12 months total
for the landings, splitting the
remaining month between those other two needs in orbit about Mars. That does cover up to two possible landing
sites in the one voyage to Mars!
The surface crew will live inside the lander on the
surface. That means it must carry
them, their exploration gear, and up to 6 months of life support supplies, on each trip.
More exploration gear could be carried to the surface if we shorten the
stay for each lander.
If four trips will be made,
that’s 3 months each (not 6), and
one can trade away life support supplies for extra exploration gear carried
down. That could cover up to four
possible landing sites in the one trip to Mars,
and each crew of 3 making 2 trips,
all with the same overall resources sent to Mars, excepting the total lander propellant supply.
Continuing that logic,
if 6 trips are planned, that’s 2
months each, each crew of 3 making 3
trips, and a higher weight of
exploration gear relative to life support supplies. That’s up to 6 separate sites that could be
explored in the one voyage to Mars! Or, 12 trips of 1 month each, which is up to 12 sites explored. Since the lander propellant is sent ahead by
SEP, it is rather easy to afford such a capability.
The biggest mass ratio-effective burn for the lander is the
ascent burn, which can be at
significantly-reduced payload, since
wastes can be left on the surface along with some exploration gear, while the weight of a plethora of samples is
far less than the weight of gear and supplies during the less-demanding
descent. That makes the overall 5.22
km/s delta vee far more affordable with an overall realistic mass ratio and
storable propellant specific impulse (Isp).
Those considerations very dramatically impact and constrain
the design of the lander.
Sending Assets Ahead Unmanned
The unmanned transfers can be done more efficiently (lower
total mass to be launched) with solar electric propulsion (SEP). The manned transport uses short-burn chemical
rocket propulsion to avoid long spiral-out/spiral-in times. (An SEP-based transport would give the crew a
lethal radiation dose spiraling-out through the Van Allen belts on departure
from Earth, and again spiraling-in
through the belts on return to Earth.) At
least approximately 0.1 gee vehicle acceleration is required to qualify as a gravity
loss-free “short burn”.
This prepositioning of assets at Mars using SEP was also a
part of my 2016 Mars mission posting. The
differences here are that I recover the SEP “tugs” for reuse on future missions, and that I use a larger “hab” for the orbit-to-orbit
transport.
Earth Departure of Manned Transport
The Earth departure can be done with higher-performing
LOX-LH2 tankage and engines on one end, that are staged off after the burn. To recover these, a higher aphelion orbit with a 2 year period
is required, plus some sort of
propulsion to return to Earth orbit. This
could be electric, or some storable
propellant rockets. (Expecting LOX-LH2
cryogens not to evaporate over a 2 year period is just nonsense!) I did not include that here, but it is required for more reusability. That’s a future growth item.
Velocity Requirements for the Mission
The orbital mechanics of min-energy Hohmann transfer
determine the minimum velocity requirements for the manned (and unmanned) vehicles, as well as the one-way travel time. Shorter flights require more energy, which is more propellant and tankage that
must be sent to low Earth orbit and assembled.
The basic velocity requirements for the manned orbital
transport are shown in Figure
6. These take the form of
unfactored orbital mechanics values serving as the mass ratio-effective values
for vehicle design. This is allowable
because all these chemical rocket propulsion burns are “short” and
exoatmospheric. The resulting mass-ratio-effective
design values are given in Figure
7.
Figure 6 – Orbital Velocity Requirements For The
Orbit-to-Orbit Manned Transport
For only Mars arrival with the manned transport, there is a need for a rendezvous propellant
allowance. It is necessary to adjust
orbital position to coincide with the assets sent ahead. As a wild guess, add another 0.2 km/s delta vee to the value
shown in Figure 7 as the mass ratio-effective value for design.
Figure 7 – Design Velocity Requirements For The
Orbit-To-Orbit Manned Transport
For the assets sent ahead with SEP, design velocity requirements are much more
problematic. There are no drag
losses, but the gravity losses are
huge, since the burns are months long! For a rough rule-of-thumb estimate, just use twice the values in Figure 7. That is what I did here.
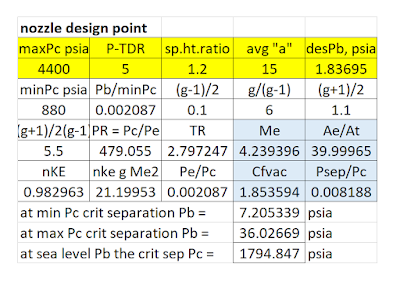
Propulsion Estimates
No particular existing chemical rocket engine’s
characteristics were used. Ballistic
estimates were made “from scratch” using shortcut methods. For both the transport and Earth-departure
engines, it was assumed that no
gas used to drive pumps was dumped overboard,
meaning 100% of the hot gas generated went through the propulsion nozzle. This requires an efficient engine operating
cycle.
Estimates were made from 1000-psia data for chamber
characteristic velocity and gas specific heat ratio, using standard ideal-gas compressible flow
methods to develop vacuum thrust coefficient (to include the effects of a
nozzle kinetic energy efficiency reflecting streamline divergence). The c* and r “constants” vary with chamber
pressure in a way that conforms to empirical ballistic methods I have long used
successfully.
This gets us to specific impulse (and thus effective exhaust
velocity) for vehicle mass ratio determinations with the rocket equation dV =
Vex ln(Wig/Wbo). The actual design
thrust level is driven by vehicle mass and the min 0.1 gee acceleration
requirement, which sizes throat (and
exit areas) via the thrust/throat area/thrust coefficient equation F = CF
Pc At. That leads to real engine
dimensions. For
not-quite-the-highest-tech in engine design technology, a good “wild guess” for engine weight would
be thrust/50, both in force units, figured at 1 gee Earth gravity for the weight.
Assuming redundant engines for safety and reliability, these rockets won’t be simultaneously run at
full thrust. For vacuum-only
operation, there is no need for really
high chamber pressure, and there is no
need to worry about backpressure-induced separation effects, because there isn’t any backpressure. 6-7 mbar on Mars is also effectively no
backpressure at all, so the lander
engines can be the same vacuum design as the transport engines.
Reflecting those considerations, I assumed 1000 psia at max thrust, typical operation at 500 psia, and min throttled-down pressure 200 psia. Others may disagree, but that is what I did. The higher the Pc, the higher the c*, and thus the higher the Isp. But so also the higher is the weight of the
engine.
The data I got for the NTO-MMH storable transit engines are
given in Figure 8. The data I got for the LOX-LH2 Earth
departure engines are given in Figure 9. For both I
assumed an expansion bell equivalent to a constant 15 degree half-angle conical
bell, leading to a kinetic energy
efficiency of 0.983 for the nozzle efficiency.
Any real-world curved bell will have an average half angle not far at
all from that value; it will be slightly
shorter than the equivalent conical bell,
and just about the same efficiency.
Figure 8 – Ballistic Estimates For Storable-Propellant
Transit (and Lander) Engines
Figure 9 -- Ballistic Estimates For Cryo-Propellant Earth
Departure Engines
The solar electric propulsion is more problematical in its
characteristics, it being currently available
only in small sizes, with scaleup
efforts underway at both Ad Astra and NASA.
What is important for vehicle design purposes would be thrust/weight for
the actual electric thruster equipment,
its operating specific impulse,
its electric power/thrust requirement,
and the type and phase of its propellant (liquids or solids are easier
to store at lower total tankage weight than gases).
Add to that the producible electric power/panel area, the weight/panel area, and miscellaneous equipment weight (if
any), for the solar power supply
equipment, and for autonomous robotic
vehicle guidance. The size of the
thruster’s thrust relative to the full vehicle weight should probably fall near
what the current small thrusters on satellites use: something near or above 0.001 gee.
Here are the values for the putative system I “chose”, it being something that does not yet exist, but likely could be made to exist near-term. Bear in mind the available solar power at Mars
is half that at Earth (Mars actually sizes the panels). The value shown for electric power/area of
solar panel is for near-Earth space,
turned to face the sun directly. This data represents a Hall-effect device
on iodine.
SEP Items Data Table
The solar photovoltaic power per unit area was estimated as
the solar constant at Earth (in space 1353 W/m2) multiplied by a 20%
conversion efficiency of sunlight power to electric power. That represents a
high-tech space-industry type of solar cell.
The weight was estimated from reported data for the Alta Devices Alta
5x1 2J and Alta 5x1 1J satellite solar panel devices. The miscellaneous equipment is not
structure, that is in the weight/area
figure for the panels. It is the mass of
the autonomous guidance equipment,
including things like star trackers,
computers, communications, and accelerometers.
Space Hab for the Crew:
Characteristics
I based these guesses off the Bigelow Aerospace B-330 space
station module design as seen on the internet (ref. 2).
This is the big commercial product,
not the simple, small BEAM unit
attached to ISS for testing and evaluation by NASA. These are nominally 15.7 m long and 20 metric
tons. They are somewhat inflatable, and feature a core equipment and framing structure
around which the inflated hull is unobstructed. There is a meter of layers of micrometeoroid
shield that also serve as thermal insulation,
and as low-molecular-weight radiation shielding. Each module contains some 330 cubic meters
of interior space. The hard core protrudes on one end, providing a place for solar panels.
The modules of the orbit-to-orbit transport cannot be
exactly these B-330 modules, but can
be something rather similar! Docking
multiple modules end-to-end creates the baton-shaped vehicle this mission
design needs. The modules must have
external features of some type that allow tankage to be attached around the
outer periphery, and internal fold-out
decks as part of the core. The center
module must be very stout, and contain
big electrically-driven flywheels for vehicle spin-up and spin-down, plus places to dock space capsules.
It would seem wiser to put big solar panels on the center
module, with the docked capsules, and the flywheels inside, where spin forces are zero-to-minimal. It is likely to be hard shell, not an inflatable, for strength.
That module is also likely to be quite heavy. As a wild guess, call it 16 m long and 40 tons. The others can be nominal 16 m long, and nearer 20 tons, reflecting inflatable pressure shell along almost
the entire length, plus the features for
attaching external tankage. Call the
internal volume 350 m3 each as a best guess, excluding what the hard core occupies.
Counting the center module,
some 7 modules each 16 m long docked end-to-end is 112 m long, for 1 full gee at each end if spun at only 4
rpm. That basic structure would total 160
metric tons, using the guesses in
the previous paragraph. To that one must
add masses for crew and 2 space suits each,
their personal effects, and personal
equipment (call it 0.5 metric ton per person as a guess), and for fully-expendable supplies of
food, water, and oxygen (call it 0.75 metric tons per
person per month, knowing that these are
just “reasonable guesses”). Crew and
supplies must fit within the vehicle,
which has (for the 6 modules not filled with flywheels and heavy
equipment) some 2100 m3 volume.
If one assumes half the volume is packed supplies, and also a crew of 6, that leaves some 175 m3 per person
as living space available. That’s about
like 3 large living rooms in a typical middle-class house. That seems adequate at first glance, if it is well distributed, and some part of it is reconfigurable at some
level.
The crew weight allowance is 3 metric tons, and the packed supplies mass is about 4.5
tons per mission month. If the mission
is 31 months long (9 months transit, 13
months at Mars, 9 months return), that’s about 140 tons of supplies, with no margin for error. So call it a nominal 150 tons. This presumes no recycling or growing-of-food
in space or on Mars. It’s a worst-case
deal, but we can do this “right
now”.
So, the empty hab
section is estimated at 160 tons. It
gets loaded with about 150 tons of supplies,
allowing for 7.5% safety factor on supply mass, and loaded with about 3 tons of crew with
their suits, equipment, and personal effects. Fully loaded,
that’s 313 tons. That would be
crew of 6, and supplies for a 31 month
mission plus a small margin. See Figure 10. Figure 11 shows an image of the spreadsheet where these numbers
were calculated. Yellow highlighting
denotes inputs. Some selected outputs
are highlighted blue.
Figure 10 – The Estimates for the Hab Section Structure of
the Orbit-to-Orbit Transport
Figure 11 – Image of Spreadsheet Used to Determine Hab
Section Characteristics
Assumed depleted at a constant rate, the supplies total 150 tons at
departure, 109.5 tons at Mars
arrival, 51.0 tons at Mars
departure, and not-zero at 10.5 tons at
Earth arrival, assuming the safety
margin is not consumed. This presumes
wastes are dumped overboard with no recycling at all! This dumping reduces the effective mass of
the hab section, at each mission segment, a benefit to propellant required.
We can already do somewhat better than that with recycled water, but this is a worst case estimate! Yet this open-cycle assumption gets the smaller
propellant supply for return to Earth.
“Efficiency” is not always beneficial: that is too often presumed erroneously! Jettisoned mass reduces next-burn propellant
requirements. That’s just physics you
cannot fight!
Sizing the Manned Transport and Its Return Propellant
The fundamental notion for sizing propellant supplies for
the four events (Earth departure, Mars
arrival, Mars departure, and Earth arrival) is that the mass of the
loaded, crewed hab, plus the mass of all propellant tankage, plus the mass of the engines, is the ignition mass. That minus the mass of propellant burned from
that tankage is the burnout mass. That
produces a mass ratio for the burn, and
the delta-vee it will produce, which
must meet or exceed the requirement for that burn. This is subject to the constraint that we
want 0.1 gee or thereabouts as a min vehicle acceleration at each burn.
To do this, one must
estimate the ratio of propellant to loaded tank mass for the added
tankage. This has to reflect a
long, slim tank geometry for docking
multiple tanks around the periphery of the hab,
and it must account for the mass of the docking structures needed to
achieve that result. As a guess, I am assuming that the empty tank inert mass
(with all those fittings) is 5% of the loaded tank mass, so that the contained propellant is 95% of
the loaded tank mass.
To that end, I used a
series of calculation blocks in a spreadsheet worksheet to run the
calculations. Again, inputs are highlighted yellow, and significant outputs are highlighted
blue. Figures 12,
13, and 14 show the results.
Bear in mind that the loaded tank mass for the Mars and
Earth arrival burns must be part of the “payload” for the Earth and Mars
departure burns, respectively. They are unique in this way. That means the dead-head payload is the
appropriate hab mass plus the mass of the next burn’s loaded tanks. The current burn’s tanks must push this (plus
the added engine mass) to the required delta-vee for that burn.
Added engine mass is handled by an iteratively-applied
tankage scale-up factor just slightly over unity.
Figure 12 – Part 1 of Orbital Transport Propulsion Sizing
As it turns out,
finding the propellant tankage mass to push the hab to the required
delta-vee is not an excruciating iterative process. You first find the mass ratio MR that is
required from the required mass ratio-effective delta-vee, and the propulsion’s effective exhaust
velocity, by the rocket equation. Ignoring the mass of the engines
themselves, it turns out to be closed-form
to find the loaded tankage mass Wtf from that mass ratio, and the total “dead head” mass to be pushed in
that burn.
For both departures,
the “dead head” mass is the appropriate loaded hab mass plus the loaded
mass of the corresponding arrival tankage.
For both arrivals, the “dead
head” mass is just the loaded hab mass.
This can be corrected at the 1 or 2% level for total engine mass
later, to ensure fully meeting the
delta-vee requirements, simply by
scaling up the loaded tank mass Wtf with a factor applied iteratively until
delta-vee produced meets the requirement.
Wtf =
Wdead (MR – 1)/(1 – MR f) where f =
Wt/Wtf and Wt is dry tank mass
Figure 13 – Part 2 of Orbital Transport Propulsion Sizing
Figure 14 – Part 3 of Orbital Transport Propulsion Sizing
That’s the orbital transport rough-out design for Mars. It can get there to low Mars orbit from low
Earth orbit where it was assembled. It
can rendezvous with its Earth return propellant, the Mars landers, and the Mars lander propellant supply, all three of which were sent ahead by
electric propulsion. The nonrecoverable
items are the Earth departure stage and the empty Mars departure tanks. The empty Mars arrival tanks are left in Mars
orbit. Everything else about this design
is recovered in low Earth orbit.
Note that this ship is 1413 metric tons, as assembled and loaded in low Earth
orbit, ready to go to low Mars orbit. Its use requires that some 997.26 metric tons
of loaded propellant tanks be sent ahead to Mars for the return propellant
supply. In order to actually make
landings on Mars as staged out of low Mars orbit, the landers and their propellant supply must
also be sent ahead to low Mars orbit.
With much bigger propellant tankage, this same design could take men to a
near-Earth asteroid. For such
missions, landers are not needed, and there is no practical opportunity to
pre-position return propellant, except many
years ahead. Those missions are far
more difficult. Analysis of one is not
attempted in this posting.
Sizing the Lander and Lander Propellant Supply
The lander payload is its crew, their suits and personal equipment, plus an amount of life support supplies that
depends upon how long the crew will live in the lander on the surface, each landing.
The de-orbit burn for a surface-grazing ellipse is a trivial 50 m/s
delta-vee. Most of the deceleration is
aerodynamic drag, effectively terminating
at end-of-hypersonics at Mach 3, just
about 1 km/s velocity, but at a low
altitude because of the high ballistic coefficient. That altitude is only about 5 km!
From there,
deceleration is by retropropulsion alone, with a large “kitty” to cover hover and
divert requirements. Assuming 1 km/s
velocity at 5 km altitude, along a
straight slant trajectory at 45 degrees,
the average deceleration level required is 70 m/s2, or 7.211 gees, which with the lander mass, sets the required engine thrust level for
landing. That is a rough ride, about twice the rigors of return from low
Earth orbit, and justifying all
by itself the maintenance of full crew health with artificial spin gravity!
The lander is a one-stage reusable “landing boat” intended
to make multiple flights, each fueled
from a propellant supply sent with it to low Mars orbit. Factored,
the mass ratio-effective descent delta-vee is just about 1.5 km/s. Propellant is storable NTO-MMH, to preclude evaporation losses and massive energy
requirements to prevent freezing or boiling.
The ascent must account for small but non-zero gravity and drag losses
(about 2% of velocity), and a “kitty”
for rendezvous maneuvers. That mass-ratio-effective
delta vee is just about 3.62 km/s.
The payload requirements for crew, equipment,
and supplies as a function of surface duration are given in Figure 15, along with a crude estimate of the “larger-than-minimum”
vehicle inert weight fraction that is appropriate to the necessary structural robustness,
and to the equipment required to
function as a reusable entry-capable vehicle,
and as a surface habitat.
Conceptually, the lander is
sketched in Figure 16. Some of its backshell panels double as cargo
load/unload ramps. Most of the cargo
space can be isolated and pressurized as living space, once unloaded. The piloting cabin is the abort capsule, something somewhat similar to a crew Dragon
from Spacex. This thing is NOT a
minimalist lander the way the Apollo LM was.
Figure 15 – Payload Requirements Vs. Surface Duration
Figure 16 – Conceptual Sketch of Reusable “Landing Boat”
The ascent payload is smaller, since most (but not all) the supplies are
used up (and wastes left behind) at ascent liftoff. There is a generous allowance for Mars
samples to be returned to the orbital transport. This has to be taken into
account in calculating the actual vehicle masses, since the two delta-vees are handled at two
different payload fractions, in the one
vehicle design. That process is
inherently iterative, as shown by the
data given in Figure 17.
Figure 17 – Iterative Determination of Lander
Characteristics vs Surface Duration
In order to determine these numbers, one guess a value for the max lander
mass, which is ignition-at-descent (Wig-des). The inert fraction times this gives the
vehicle inert mass Win. The ascent and
descent payloads are determined vs mission surface duration separately. The mass ratios already determined are used
to estimate propellant masses.
The ascent propellant mass Wp-asc is determined first as
(MR-asc – 1)(Wpay-asc + Win), then the
descent propellant mass Wp-des as (MR-des – 1)(Wpay-des + Win + Wp-asc), treating the ascent propellant as part of the
effective “payload” during descent. The
descent payload plus both propellant masses plus inert mass sum to the result
for descent ignition mass.
The input guess for descent ignition mass is then adjusted
iteratively, until it converges to
the result for descent ignition mass.
This is done by simple trial and error in the spreadsheet. There is such a result computed for each of 4
possible surface durations that divide evenly into the 12 months
available. These results are then the
inputs for a characterization of the lander sizing as a function of design
surface duration.
For the selected 2-month duration (corresponding to 6
total lander flights), those results
are given in Figure 18. These show ascent and descent weight
statements, confirmation of delta-vee
capability, and characterization of
vehicle mass fractions, plus the
propellant supply required to cover the appropriate number of flights. Similar tables exist in the spreadsheet for
the other 3 durations, but those are not
shown here.
Figure 18 – Lander Design Characteristics for 6 Flights of 2
Month Surface Duration Each
Figures
19 and 20 show the trade-off of vehicle sizes and propellant supply
sizes versus surface duration options. The
selected design is near the “knee” in the curve of number-of-flights vs surface
duration, at 2 month duration for 6
flights. For shorter duration, the required propellant supply is
significantly larger. For longer
duration, the required propellant supply
is smaller, but not so significantly
smaller.
The lander size itself is significantly affected by the
design surface duration, being larger at
longer duration. The 2-month duration
selected limits this affect, without so
significantly penalizing the payload fraction (which ranges from about 2 to
about 3%). The selected 2-month duration
is also near the “knee” in that curve.
Longer durations do not improve this as much as was gained going from 1
month-12 flights to the selected 2 month-6 flights option.
Figure 19 – Number of Landings and Required Propellant
Supply Vs. Surface Duration
Figure 20 – Lander Size and Payload Fraction Vs. Surface
Duration
For this selected design (6 two-month surface stays), three landers fueled and loaded with
supplies, less crew, suits,
and personal equipment, each
massing 376.5 metric tons, must be sent
to Mars along with some 1764 tons of propellant to support all 6 flights. If 95% of the tank weight is propellant, the mass of loaded tankage to be sent is some
1856.8 metric tons. If sent as tanks
docked to each of the 3 landers, that’s
a 376.5 ton lander plus 619 tons of loaded propellant tanks.
The “smart” thing to do from a reliability /
self-rescue standpoint is to send the transport return propellant with those
same three landers, so that if one is
lost, the transport can still return
safely by drawing the shortfall instead from the remaining lander supplies. That return propellant was determined above
to be 997.26 metric tons of loaded tanks.
Divided by 3, that’s an
additional 332.4 metric tons of Earth return propellant tankage sent to Mars
with each lander.
That makes each lander plus propellant tanks a 1327.9
metric ton item to be moved by solar electric propulsion from low Earth orbit
one-way to low Mars orbit. Each
such is thus quite comparable to the departure mass of the manned orbital
transport. That would not be true
at the other surface durations.
There are 6 landings to be made, and three such landers sent to Mars. Distributed evenly, that is two flights per lander minimum, and 6 maximum. Bear in mind that only one lander is sent to
the surface at a time, carrying a crew
of 3, while the other three crew do
science in orbit, while acting as the
safety rescue “watchdog”, with at least
one functional lander, even if the other
one fails. The worst case is that all 6
flights are made with one lander. Thus
the lander design must allow for at least 6 flights per vehicle, justifying in part the higher inert mass
fraction used in this design rough-out.
Landers get left in low Mars orbit at mission’s end, when the transport departs for Earth. Subsequent missions might utilize these
assets, and reduce the sent mass to only
more lander propellant. That
possibility argues for much more than 6 flights per vehicle, in turn a really good argument for the very
robust inert mass fraction of 20% used here. Alternatively, they could be landed robotically.
Common Engine Design for Transport and Lander?
The lander mass is 378 metric tons at ignition, and 241 at touchdown, as just determined above. The average is 309.5 metric tons. Also as determined above, the average deceleration required is 70 m/s2. That translates to 21,665 KN of
retropropulsion thrust required to safely land (nominally 22,000 KN). This is totaled for multiple engines. Less may be used for ascent, as such high gee capability is not required
for that. Something nearer 2 gees at ascent
ignition mass 236.3 metric tons (4726 KN thrust) is more appropriate.
As described above,
something near 1170 KN thrust from multiple engines is the minimum
required for the orbit-to-orbit transport.
This was set by the min 0.1
vehicle gee capability at max vehicle mass,
and still resulted in only large fractional gee capability at min
vehicle mass. This thrust level
selection could be doubled or tripled (or more) with relative impunity.
A worksheet page was set up in the spreadsheet to explore
how this could be done, in two
steps. The results are shown in Figure 21, which indicate the possibility of using some
number of 3600 KN max thrust engines,
throttleable from 20 to 100%. In
the first step, I input factored thrust
requirements, plus a number of
engines, and a max number of inoperative
engines.
The thrust requirement for the lander descent is based on
slowing the average descent mass (as a constant) from 1 km/s to zero, in a slant path length of 7.1 km, using the oversimplified kinematic equation V2
= 2 a s. This is a very high-gee
descent! Reducing that requires
not just supersonic retropropulsion, but
hypersonic retropropulsion (starting retropropulsion earlier in the entry
sequence). It is an inevitable
consequence of the high ballistic coefficient producing very low altitudes (on
Mars) for end-of-hypersonic deceleration.
This is an area for further design work!
The thrust requirement for the lander ascent is its Earth
weight, factored-up just slightly, to accommodate flight tests on Earth. That’s “overkill” for Mars with its lower
gravity.
The thrust requirement for the orbital transport is based on
its Mars departure mass (largest of the masses under storable propulsion) and a
min 0.1 gee vehicle acceleration requirement.
This is arbitrarily factored-up by 3 to achieve commonality, without exceeding max gees ~ 2 at Earth
arrival.
That initial result indicated that something like 3600
KN max thrust per engine would be suitable, with 9 engines in the lander operating at
part throttle in descent, and 4 engines
operating at part throttle in ascent,
able to lose up to 3 engines either way,
and still function within limits.
This was explored further,
looking at vehicle gees and engine throttle percentages, in the second step.
Up to 3 of these lander engines could cease operation during
ascent or descent. The remainder could
supply adequate thrust at 100% throttle or less, without waiting for lightoff of any
inactive engines. That’s an important safety consideration, which ethics demands! Two of these same engines would be adequate
to push the orbital transport at part throttle,
with only one operating engine still able to supply much more than the
demanded minimum thrust.
Figure 21 – Determination of Size and Distribution of a
Common NTO-MMH Engine Design
In all cases, engines
operate between 20 and 100% throttle setting,
and appropriate gee limits are not exceeded. Min transport vehicle gee requirement (0.1
gee) is exceeded.
For descent, the
lander retropulsion operates between about 6 and about 9 gees. This event is only about 14-15 seconds
long!!! “At the last second” to
actually land, some 8 of the 9 engines must
be shut down to reduce thrust to nearer Mars weight of the lander (about 749 KN
to 872 KN, depending upon how much
propellant was burned) at touchdown,
with the remaining active engine operating at about 21-24% thrust
setting. This single-engine point is the
riskiest aspect of the landing, but it
is mitigated by the facts that (1) this engine is already operating, and (2) it need only continue to operate at
reduced thrust for a second or two.
On ascent with a reduced number of engines, this is 1.2 to 3.6 gees for the lander at
full thrust, far more than is needed to
depart against Mars gravity (only 0.38 gee).
Active throttling reduces that some.
The transport operates between 0.3 and 1.8 gees during the
return to Earth. This exceeds the min
acceleration requirement, but not the
maximum. A 3600 KN engine design for
this NTO-MMH common engine would resemble the notional sketch in Figure 22.
If the Earth departure stage at 1350 KN uses 5 engines, each would be approximately 1350 KN max
thrust capability operating at 20% thrust.
Up to 4 could be non-functional,
and still easily meet the overall min departure thrust requirement, without exceeding 100% throttle. Higher vehicle acceleration than 0.1 gee is
easily obtained, but even with all 5
engines at full thrust, it is still only
fractional gee. Such a 1350 KN LOX-LH2
engine would resemble the notional sketch in Figure 23.
Figure 22 – Sketch of Proposed 3600 KN NTO-MMH Common Engine
(one of 2 transport, 9 lander)
Figure 23 – Sketch of Proposed 1350 KN LOX-LH2 Earth
Departure Engine (one of 5 on the departure stage)
Sizing the SEP for the Unmanned Assets Sent Ahead
This item is the most speculative, because (1) it uses the most assumed
data, and (2) this kind of solar
electric propulsion has yet to be scaled up to such sizes to push masses this
large. To cover the gravity losses (both
planetary and solar), I simply doubled
the required orbital delta-vee data.
I simply assumed the average characteristics of small Hall
effect thrusters operating on iodine could be scaled way up by simple
clustering, at the same thrust/weight
and thrust/power ratios. And, I just assumed the characteristics of
satellite-sized solar panels could be scaled up to the low-hundred kilowatt
range at the same power/area and weight/area ratios.
My approach was a self-contained solar-electric propulsion
(SEP) “tug”, that incorporates the
clustered thruster unit, the solar
panels to power it, sized for reduced
sunlight at Mars, a robot guidance
package, and a low-pressure “tank” to
contain the easily-sublimated and
inexpensive iodine propellant. I used
published data for two Busek Hall-effect thrusters, and for a couple of Alta Devices satellite
solar panels, for these estimates.
This SEP “tug” is coupled to a dead-head payload for the
trip from Earth orbit to Mars orbit,
using all of its 120 clustered SEP thrusters to achieve a milli-gee of
vehicle acceleration capability at Earth departure. That payload is one (of the three) Mars
landers (fully fueled and supplied),
plus a 1/3 share of the total lander propellant supply, and plus a 1/3 share of the manned orbital
transport’s Earth return propellant supply.
This dead head payload is over 1300 metric tons.
For the return trip (these “tugs” are fully reusable), there is no dead-head payload, only the “tug” and its iodine tank, still containing just enough iodine
propellant to get home. During the trip
home, only one SEP thruster in the
cluster need be used to achieve near a milli-gee of vehicle acceleration at
Mars departure. That leaves many “spares
in case the one fails”, insuring utter reliability. (Outbound,
the cluster is large enough that the loss of a few thrusters is no significant
percentage loss of thrust.)
The size of one such thruster (200 mN, mN meaning milli-Newtons) falls within the
range of thrusters produced today. This
produces adequate acceleration of the unladen vehicle. The scaleup is by clustering, not by increasing the size of the thrust in
such a device. The clustering-together
of 120 of these units produces some 24,000 mN,
needed to move the laden vehicle at adequate acceleration.
The resulting SEP “tug” design is depicted in the sketch of Figure 24. I used a big two-stage spreadsheet worksheet
to iteratively size this “tug” system,
examining the 4 “burns” individually.
The second stage of this process fully defines the characteristics of
the “tug” and its estimated performance.
This is the tabular data in the partial spreadsheet image shown in Figure 25.
Hopefully, this
rough-sizing is “overkill”, due to my just-assumed
doubling of the orbital delta-vee requirements.
The intent here is to slowly spiral-out of low Earth orbit to
escape, and continue an accelerating
spiral about the sun to an appropriate midpoint, then use a decelerating spiral about the sun
toward capture at Mars. From there, it follows a decelerating spiral-in to low
Mars orbit. The return uses the same
spiraling processes, just unladen of
dead-head payload, and at far-lower
thrust and propellant requirements.
Figure 24 – Depiction of the SEP “Tug” Design Sizing
Rough-Out
Figure 25 – Partial Spreadsheet Image Showing “Tug”
Characteristics and Performance
Sizing the Earth Departure Stage
Of all the items analyzed,
this is the easiest and most straightforward, because there is one and only one burn (the
Earth departure burn). Then this stage
is jettisoned. The stage layout concept
and sized data were already determined as part of the orbital transport
propulsion sizing above. These data were
given as part of Figures 12, 13, and 14 above,
plus part of the common engine discussion just above, with sized engine dimensions in Figure 23.
Just to summarize,
the departure stage has 5 LOX-LH2 engines each designed for 1350 KN
thrust, weighing an estimated total of
5.139 metric tons. The stage comprises
LOX and LH2 tankage whose combined dry weight is 41.906 metric tons. The total propellant load is some 796.210
metric tons. Thus the loaded stage
itself is some 843.255 metric tons.
This stage pushes a fully loaded and crewed hab plus Mars
arrival propellant tankage that totals some 569.810 metric tons of dead-head
payload. Total orbital transport vehicle
mass, at Earth departure ignition, is thus some 1413.065 metric tons. This was shown in Figure 14 above, including weight statements and performance.
Not considered here is reuse of the Earth departure
stage. Its engine sizing would be
fine, but it needs larger tanks and
propellant to accomplish 2 burns. The
first is to put the orbital transport onto a Hohmann transfer ellipse
trajectory.
After releasing the transport, it burns a second time to enter an ellipse
about the sun with an exactly two-year period.
That way the Earth is there when it reaches perihelion, thus making recovery feasible at all.
It is just not reasonable to expect that cryogens like LOX
and especially LH2 will not completely evaporate away over a 2 year
interval. Therefore, the reusable form of the stage must also
incorporate a second propulsion system storable over long periods. This added propulsion provides the delta-vee
to return to Earth orbit from the 2-year solar orbit perihelion conditions.
Being unmanned, there
is no reason this second propulsion system could not be solar-electric using
iodine. The stage then executes a
spiral-in to low Earth orbit after capture.
The alternative is storable propellants like the NTO-MMH.
Being out of scope here at this time, these designs have not been explored. Consider that as a future upgrade.
Totaling Up the Mission and Its Launch Requirements
This mission to Mars requires a fleet of 4 vehicles to be
sent from Earth orbit to Mars orbit. One
of these (the manned vehicle) returns to Earth.
The other three are unmanned assets sent ahead earlier by electric
propulsion, for the crew to utilize when
they arrive by conventional rocket propulsion.
The three unmanned vehicles are identical, comprising a dead-head payload and a reusable
solar-electric “tug” that returns to Earth for reuse, after delivery of the dead-head payload into
orbit at Mars.
That dead-head payload payload is the same for each of these
vehicles: an uncrewed but loaded and
fueled reusable Mars landing boat, plus
1/3 of the total Mars lander propellant supply,
plus 1/3 of the crewed vehicle’s Earth return propellant supply. That dead-head payload is 1327.9 metric tons
for each of these 3 vehicles.
Each of these three unmanned vehicles totals some 2413.5
metric tons as assembled in Earth orbit,
that being the dead-head payload plus the fueled SEP “tug”.
The crewed vehicle (the orbit-to-orbit transport) comprises
the crewed and loaded hab section, plus
the loaded Mars arrival propellant tankage,
plus the expendable Earth departure stage that uses cryogenic
propellants. (All the other rocket
propulsion uses the same storable propellants,
and the SEP “tugs” use sublimable iodine to keep the iodine “tank”
weight down.) Ready to depart Earth
orbit, the transport and departure stage
total some 1413.065 metric tons.
The grand total that must be assembled in orbit for the
fleet of 4 ships is some 8653.6 metric tons.
For that, you get 6 landings at
up to 6 different places on Mars, all in
the one manned trip to Mars. That’s
1442.3 tons to support each of the 6 landings,
essentially. These are 2-month
max stays at each landing site. You get all this, plus a “way out” or a self-rescue capability
built into the mission at every step,
plus a fully-healthy crew with radiation shielding and artificial
gravity during the transits, and in low
Mars orbit. That’s a lot of benefit for the cost.
Getting
Landers To Low Earth Orbit
The selected lander design is just about 378 metric
tons, crewed, loaded and fueled. Less crew (and their suits and gear), that’s just about 376.5 metric tons. Just about 294 tons of that lander weight is
propellant. So, a loaded,
crewless, empty-of-propellant lander
is just about 82.5 metric tons. Remove
the supplies, but leave the surface
equipment and rover aboard, and this is
about 77 tons. Completely unladen, the lander is about 75.6 tons.
I looked at SLS (150 metric tons to LEO, guessing $1,000M per launch), Spacex’s “Starship” (100 metric tons to
LEO, guessing $150M per launch), Spacex’s Falcon-Heavy (63 metric tons to LEO
flown expendably, about $85M per
launch), ULA’s Atlas-V (20 metric tons
to LEO at about $85M per launch), and
Spacex’s Falcon-9 (20 metric tons to LEO flown expendably, and $63M per launch).
The loaded unfueled lander mass of 75.6 metric tons is out
of reach of Falcon Heavy, much less
Atlas V or Falcon 9, even if an 8-meter payload
diameter could be flown on any of them. NASA’s
SLS might possibly launch it dry of propellant,
maybe even two of them at once, although
it has yet to fly. That would be 2 or 3
flights of SLS at $2-3B to put 3 landers into orbit, unladen of propellant. It would be 3 flights of “Starship” at $450M
total. The most cost-effective of those
two options is “Starship”. 3
“Starships” deliver 3 landers loaded but unfueled.
At 294 tons of propellant per lander, and 100 tons per “Starship”, some 9 “Starship” tanker flights would be
required to fuel them fully up. At 150
tons per SLS, some 6 SLS flights would
be required to fuel them up fully. At
about 60 tons per flight, some 5 Falcon
Heavy flights could be those tankers per lander, for some 15 Falcon-Heavy flights to fuel the
3 landers up. At 20 tons per
flight, it would require some 45 flights
of Falcon-9 or Atlas-V to fuel the 3 landers in orbit. The most cost-effective way to deliver
these bulk liquid propellant supplies turns out to be 9 “Starship”
flights, with 15 Falcon-Heavy flights a rather
close second. If “Starship”, the transfer crew need not be sent up
separately.
Getting
Earth Return and Lander Propellant Supplies to LEO and Docked
Remember, we must
send to Mars each lander loaded and fueled,
plus 1/3 of its Mars landing propellant supply, plus 1/3 of the transport’s Earth return
propellant supply. These propellant
supplies are pre-loaded tanks. They are
1764.1 tons for the lander operations,
541.3 tons for the transport’s Mars departure, and 455.9 tons for the transport’s Earth arrival. That totals some 2761.3 metric tons of
propellant, which must be in tanks, at about 95% propellant and 5% tank inert.
Unconstrained by other considerations, I chose to break this up into nominal 60-ton
loaded tanks. The lander supply is 31 of
these, the Mars departure supply is 10
of these, and the Earth arrival supply
is 8 of these. That’s a total of some 49
tanks to deliver to LEO, at 60 metric tons
each. The most cost-effective way
to do this was 49 flights of Falcon-Heavy,
flown expendably.
We will need a docking crew on-orbit for about a week max to
assemble the docked cluster for each of the landers. This can be a crew of 2 to 4 in a Crew Dragon
atop a Falcon-9. This probably will not
happen in parallel for the 3 landers,
but serially. So plan on 3 manned
Falcon-9 launches to support these assemblies.
Getting
the Transport to LEO, Loaded, and Assembled
The orbit-to-orbit transport goes up as separate modules
(without supplies) to be docked in orbit.
There are six 20-ton modules and one 40-ton center modules, complete with solar wings that must
unfold. All the listed boosters could
launch the 20-ton modules, only Falcon-Heavy, “Starship”,
or SLS could launch the 40-ton module.
The most cost-effective means was a tie: 2 flights of “Starship” or 3 flights
(expendable) of Falcon-Heavy deliver these 7 modules to LEO.
There is about 150 tons of supplies, crew suits,
and crew personal equipment to deliver to the transport and load inside
(152 exactly, per these
admittedly-uncertain estimates). This is separable into lots deliverable by any
of the boosters listed. From a
cost-effectiveness viewpoint, this was
another tie: 2 flights of
“Starship”, or 3 expendable flights of
Falcon-Heavy.
This is going to require a temporary docking and loading
crew of perhaps 4 to 6 astronauts for a week or so in orbit. If we send them up in two Crew Dragon
capsules atop Falcon-9 boosters, they
can come home in one, and leave the
other Crew Dragon docked to the transport as one of its emergency return escape
craft. Add 2 Falcon-9 flights for
the transport assembly crew unless “Starship” is used instead.
Getting
the SEP “Tugs” to LEO and Fueled
The SEP “tug” hardware,
empty of the solid iodine fuel,
are not heavy at all. This crude
estimate says they are 14.42 tons each,
and there are 3 of them. That includes the folded solar panels, the big thruster array, the guidance package, and the empty tank which doubles as the
vehicle core structure, about which
dead-head payload gets docked.
Any of the listed boosters can get an empty tug to LEO. The most cost-effective means is 3
Falcon-9 launches, possibly flown
recoverable, but the expendable price
was used here.
The iodine thruster fuel is a sublimable solid, which can be sent up in portions that fit the
various boosters, determining the number
of flights. For the three tugs
together, we need 3213.54 metric tons of
iodine sent to LEO. (Most of this, by far,
gets used sending payload to Mars.
Only a few tons with only 1 thruster firing is needed to return to
Earth.)
Any of the listed boosters can do this job. The most cost-effective means is by
“Starship”, with Falcon-Heavy a close
second. That would be 33
“Starship” flights, or 54 Falcon-Heavy
flights flown expendably.
It will take a crew of 4-6 astronauts to load the iodine
fuel and unfold the solar arrays, plus
some checkout. We probably do not do all
3 vehicles in parallel, but
serially. If by “Starship”, that vehicle can carry the crew. If by Falcon-Heavy, a separate Falcon-9 launch is needed to send
this crew up for a week or two in orbit as the payloads arrive, which is a huge Falcon-Heavy flight rate! “Starship” with payload and loading
crew aboard is thus the preferred way,
by far.
Getting
the Earth Departure Stage to LEO and Fueled
This is assumed an empty stage delivered as one piece of
hardware at 47 metric tons, plus 796.2
metric tons of LOX-LH2 propellants delivered as bulk liquid. Bulk liquids can be delivered in multiple
payloads by any of the listed boosters,
but requires special tankage and a human crew to do the transfers.
The most cost effective way to deliver the empty stage
is by a single Falcon-Heavy, possibly
flown recoverably, but priced expendably
for this analysis.
The most cost-effective means to deliver bulk propellant is
8 “Starship” flights, followed fairly closely
by 14 Falcon-Heavy flights. These
require crews, which can be aboard the
“Starship” flights. They would have to
come up in some 14 Falcon-9 launches with Crew Dragon if Falcon-Heavies were
the propellant ferries. By
far, the preferred approach is 8 crewed
“Starship” flights.
Getting
the Crew Onto the Transport for the Mission
The Mars mission crew is only 6 people. This is one Falcon-9 Crew Dragon flight
to send them up. Their Crew
Dragon docks with the transport to be its second (and redundant) emergency
escape capsule. If not covered earlier,
make this 2 flights so there are two Crew Dragons as escape capsules.
Totaling Up Mission Launch Requirements & Guessing
Costs
I totaled-up the launch costs for this mission. On the assumption that launch costs are 20%
of overall program costs, that puts this
mission in a rather modest cost category,
despite the large tonnages. That
is precisely because it does NOT use SLS to launch anything, at a billion dollars per flight (if not more)! See Figure 26 for a summary of the launch requirements and
costs. The basis for comparison is the
infamous “90 Day Report”, based on
mounting essentially “Apollo-on-steroids-plus” as executed by the long-favored
contractors, to send a crew of 4-to-6 to
one site on Mars, in the one trip.

Figure 26 – Rough-Guessed Costs From Estimated Launch
Requirements
Totaling Up What the Mission Accomplishes
This makes the comparison to the “90 Day Report” even more
stark. This mission as planned has a
“way out” or a self-rescue capability at every step, plus inherently designed-in artificial
gravity and radiation protection (to include solar flare events). The likelihood of this crew returning alive
and healthy is actually quite high. In
comparison, with the “90 Day Report”
mission, that likelihood is rather low, because it does not offer those
characteristics.
What this mission accomplishes is up to 6 different sites
explored in the one manned trip to Mars.
With the “90 Day Report” mission design,
only one site gets explored.
This mission leaves considerable usable assets at Mars for
future missions to utilize. That would
include the reusable landers, either in
low Mars orbit, or on the surface if
landed robotically. Plus, there might be
some leftover propellant, probably in
Mars orbit. The “90 Day Report” mission
leaves few (if any) usable assets on Mars for future missions to utilize: maybe a surface habitat structure and a rover
or two, and possibly a nuclear power
supply item.
See Figure
27 for a listing of what this mission accomplishes, compared to that of the “90 Day Report”.
Figure 27 – Mission Accomplishments and Characteristics Summary
and Comparison
“Bang-for-the-Buck” Discussion
The first gross indicator is program cost for the one trip
to Mars, divided by the number of sites
explored while the mission is there. For
my mission design, cost per site ranges
from $11.7B/site to at most $70.3B/site,
depending upon whether the minimum 1 or maximum 6 sites get
explored. That is factor 6.4 to 38.5
times better cost per site than that of the “90 Day Report”.
The second gross indicator is the likelihood of getting the
crew back alive and healthy. Because of
the features demanded by ethics, and
designed-in from the start, this mission
plan can truthfully claim a high likelihood of accomplishing this. The “90 Day Report” mission plan cannot
truthfully claim that.
For one thing, there
is no rescue for a crew stranded on Mars.
For another, there is a high
likelihood of a solar flare event during a 31 month mission, and almost zero chance of surviving that event
with no radiation shelter. And yet
another: there are two 9-month transits
in zero-gee, separated by a 13 month
stay on 38% gee Mars, with undetermined
therapeutic effect, if any. Should an emergency free return at Earth
arrival be required, that is a high-gee
event (likely 10+ gees). A crew weakened
by microgravity diseases is unlikely to survive this.
Now remember, spaceflight
history clearly demonstrates that there is nothing as expensive (economically
and politically) as a dead crew.
Especially one dead from a bad management decision. My mission design raises crew survival
probability, the “90 Day Report” mission
design does not; that survival
probability is quite low, if one is
truthful about it.
In order to get both high “bang for the buck” and a high
likelihood of getting a crew back healthy,
I had to think way outside the usual boxes. One of those boxes is “nothing can look much
different than what we already did during Apollo, shuttle,
and ISS”. Another is “no mission
can be affordable if there must be a high tonnage launched”. A third is “you simply must do direct entry
at Mars to save launched tonnage”. A
fourth is “you must use SLS no matter what in order to launch this mission”.
All proved to be false constraints on thinking. The only one that is true is the one I
used: crew survivability above all, driven by basic ethics. In a nutshell: “provide a way out or a self-rescue
capability at every single step”. That
drove me to orbital-based exploration and a manned orbit-to-orbit transport
design.
The main possible weakness of my mission design is the low
payload fraction of my one-stage reusable landers: around 2%.
A one-shot two-stage design would have a far higher payload fraction
(perhaps 5-6% if you include the safety-required abort capsule, only higher if you fail this safety
requirement), resulting in a smaller
mass sent to Mars for each lander. But I
would have to send more of them (8) to maintain a rescue capability and a
spare, and still visit as many as 6
sites. This I leave to others to
explore.
Final Comments
In terms of both cost and safety, the comparison of this mission plan to that
of the “90 Day Report” demonstrates the unattractiveness of the usual way NASA
did things in the past. There is far
more “bang for the buck” and an enormously-higher probability of getting the
crew back alive and healthy in my plan. Not only that, my program cost is far, far lower.
The astute reader will observe that I have selected a
lot of Spacex hardware as the most cost-effective means to launch and assemble
this mission. That begs a
comparison to the Spacex plan just to send multiple “Starships” to Mars by
direct entry from the interplanetary trajectory. According to the presentations released, that would be about 6 “Starships” initially landed
on Mars, with probably one or at most two
of them eventually returning to Earth,
if the local propellant production works, and it can supply them fully and quickly
enough.
It is as yet unclear whether 5 or 6 “Starship” tanker
flights are required for refueling each interplanetary “Starship” in LEO for
the journey to Mars. So somewhere
between 36 and 42 total “Starship” launches are required to support their
mission. Using $150M per launch, and launch costs equal 20% of program
cost, that’s $5.4-6.3B launch cost, and $27.0-31.5B program cost, to put their mission onto Mars.
That program cost scaleup is real, even for them, because they are counting on others to supply
the local propellant production hardware,
local rover vehicle capabilities,
and local life support capabilities (cannot live in the landed
“Starship” forever !!), not to mention
local electric power. They have their
hands full just developing the “”Starship” vehicle.
That’s comparable to my costs, and (like me) way below the costs in the “90
Day Report”. The differences are
many, however. They explore only 1 site, period.
If the local propellant production fails to meet expectations, nobody comes home. They say they will supply radiation
sheltering, but not artificial
gravity. They are counting on Mars’s
0.38 gee being “therapeutic enough”,
when in point of fact, nobody yet
knows that to be true. My mission takes none of those risks and explores
up to 6 sites.
There is no aborting or bailing-out during the “Starship”
direct entry at Mars. There is no
aborting or bailing out during the landing and touchdown. They have yet to address soil bearing loads
vs landing pad size for Mars, or rough
field landing hazards such as slope,
local roughness and big boulders. There is no bailout or abort during the
return ascent. There is no bailout or
abort for the direct entry at Earth return.
There is no bailout or abort during the Earth landing and
touchdown. A failure during any one
of these events is inevitably a loss of the vehicle and everybody aboard. My mission takes none of those risks.
Yeah, you can save
the money using “Starship” as the transit vehicle (by about a factor of 2-3
over my plan). But you are also very much
more likely to kill one of your crews if you do (which also very likely would
put a stop to the ongoing mission).
Ethics-driven spaceflight design “from the get-go” seems the
more prudent course, especially when you
consider the consequences of killing a crew.
References
#1. NASA radiation website: http://srag.jsc.nasa.gov/Publications/TM104782/techmemo.htm,
titled Spaceflight Radiation Health Program at JSC (no cited reference newer
than 1992).