Kudos to Spacex

The latest news reports indicate that the Spacex “Dragon” capsule arrived at the ISS space station in excellent condition,  and is being successfully unloaded of about a half a ton of supplies.  It’s due to come home Thursday with a similar-sized  load shipped home from the space station. 

This feat makes the history books as the first successful demonstration of commercial cargo supply capability for the ISS,  or any another space station that might appear up there soon.  If all goes well for the landing,  the test flights are over,  and Spacex is in business hauling cargo for NASA. 

Kudos to Spacex on having both the art and science of spaceflight under their belts.  This commercial cargo capability is going to transform spaceflight forever.  “Steely-eyed missile men”,  indeed!

Further,  this is a reusable capsule design.  Once routine flights begin,  I believe we will see the same capsules flown again and again to the ISS,  carrying cargo.  That will be another first for the history books.

“Dragon” was always intended to carry people,  up to seven,  the same size as a shuttle crew.  All it and its Falcon-9 booster rocket need in order to be “man-rated”,  is an escape system and a history of successful unmanned flight. 

The cargo flights to the ISS will provide that history.  The thrusters big enough for escape purposes are being tested now.  Get set for another first for the history books,  when “Dragon” flies manned. 

There will be more history-making feats by Spacex in the future,  I predict.  They are “doing it right”.

My heartfelt congratulations,  once again.

GW

Revised, Expanded Launch Cost Data

This posting revisits source data on the internet, and revises, replaces, and/or updates the data posted here earlier in “Launch Cost Data”, dated 1-9-12. To the extent possible, I used data from the websites of the actual makers of the launch vehicles. Two figures are at the end of this article.

Update 9-25-12: please see my posting dated 9-13-12, which includes estimates based on the latest NASA launch cost projections for the giant NASA SLS launch rocket.

For the Falcon series, I obtained both payload and launch cost data directly from the Spacex website, which I know to be periodically updated. I searched these data as of 5-26-12. These are for max payload delivery capability to low Earth orbit (LEO) launching eastward out of Cape Canaveral. Vehicles include Falcon-1, Falcon-9, and Falcon-Heavy, in order of increasing payload capability.

I did include the Falcon-1 data in order to see a very nonlinear 3-point curve for unit cost vs payload size. One should bear in mind that Falcon-Heavy has not been ground-tested or flown yet, although it should be flying within about 2 years.

For the Atlas-V series, I included only those configurations capable of 18 metric tons or more to LEO out of Canaveral. That gave me another 3-point curve, out on the low-slope range of the Spacex/Falcon curve. ULA’s website provided payload data on the Atlas-V-HLV (heavy lifter) configuration, and shows a copyright date of 2011. They provide no launch prices at all.

I obtained payload data on the other Atlas-V configurations, and all my launch price data, from the spaceandtech.com website. It shows a copyright date of 2001, so the price data is fairly obsolete, at least due to inflation. One should also note that the LEO payloads for Atlas-V-HLV disagree between the two websites, although the rest seems accurate. I used ULA’s data as much more recent.

The three Atlas-V configurations include Atlas-V -542, Atlas-V-552, and Atlas-V-HLV, again in order of increasing payload capability. These are the ones for 18+ metric ton capability. There are many other configurations of lesser payload.

I obtained LEO payload and price data from spaceandtech.com for the following single-point vehicle configurations: Delta-IV-H (heavy) from ULA, the no-longer-flying Titan-IVB, the Russian Proton D-1, and France’s Ariane-5. All were selected for 18+ metric ton capability to LEO, presumably eastward out of Canaveral.

The spaceandtech.com launch price data were “estimates only”, and by copyright date, are 11 years out of date. I corrected these for 11 years of annual 2% inflation, before computing unit prices for my comparisons. The Spacex website prices needed no correction, being quite current as of this writing.

What I Computed

I computed minimum unit cost for LEO payload delivery from Canaveral, by dividing launch price by the maximum payload deliverable. Unit prices this low only obtain if the vehicle flies fully loaded. To correct these unit prices to other (lower) loadouts, one must divide launch price by the lower payload loadout. It makes a “fish-hook” curve tangent to my plots, due to the 1/x effect, where x is payload.

The results I got speak to some very interesting trends. I show two figures below, one plotted as $/kg unit cost versus payload size in metric tons for my metric readers, and one as $/lb unit cost vs payload size in the same metric tons for my American-units readers. (There are 2205 lb in every metric ton. Metric tons are “just a skosh” larger than the very simple “10% bigger than a US ton”. At least that’s close enough for comparison.)

Commercial Unit Price Trends

The first thing to point out is the nonlinear trend of unit cost vs payload weight. Below about 10 metric tons delivered to LEO, this is has a high slope. Above about 10 metric tons, the slope is low, and just about the same for both Spacex’s Falcon series and the ULA Atlas-V series. The single-point spot checks of ULA’s Delta-IV and the French Ariane-5 are right in the same ballpark. Russia’s Proton D-1 falls right on top of the Spacex curve, while the others are slightly higher.

These are all launch vehicles currently competing in the commercial launch market (excepting Falcon-Heavy, which soon will). The range of prices at an arbitrary constant 20 metric tons is about $4000/kg ($2000/lb) Spacex, $5800/kg ($2500/lb) Atlas-V, and $6500/kg ($3000/lb) for Delta-IV and Ariane. In my opinion, that spread of unit prices most likely reflects how successful each company has been at simplifying the rocket and reducing the logistical support for each launch. All seem to be more or less competitive, with Spacex and the Russians seemingly the most successful at lowering costs.

Government Unit Prices

Titan-IVB is no longer being flown, and was never really used in commercial competition. That is a very important difference. This is a launch vehicle that, in my opinion, was operated and supported more like the way US (and other) government launch vehicles were operated and supported for all the decades until commercial space “took off”. The corresponding logistical tail would be enormous, and the price shows it, at something near $18,500/kg ($8500/lb).

Not shown on these curves is the unit cost of the now-retired Space Shuttle. Because it was a spaceplane, the payload delivered to orbit is a small fraction of the mass delivered to orbit. Further, it was a complicated government operation with a truly enormous logistical tail supporting it. The Shuttle delivered at most 25 metric tons to LEO, for a launch cost in 2011 dollars of about $1.5 billion. At max payload, that’s about $60,000/kg ($27,000/lb).

Those Space Shuttle unit cost points are completely off the scale of my plots here. They are one full order of magnitude larger than current unit prices for payloads in the 18-29 metric ton range. That actually means our $100 billion space station could have been far cheaper, by many factors, if launched and assembled today with these rockets.

Another major point to make is the disparity between the government way of doing things, and the commercial way of doing things. Fairly compared, we look only at expendable launch rockets, and right at 20 metric tons delivered to LEO. Titan-IVB is about 4 times more expensive, but about 2 to 3 times cheaper than Shuttle.

Interpretations

For launching 20-ton (or more) payloads one-way to LEO, it would be hard to beat the expendable launch rocket, because of its demonstrated factor 2-3 cheaper unit cost than a spaceplane, all compared as a government -type operation. Launched on commercial rockets instead, the unit cost is around 4 times cheaper still, than a government-style operation.

That is not to say that commercial spaceplanes cannot be useful, because they can. But, I suspect this will be for the much smaller payload masses, where the launch rocket curves trend much more sharply upward as delivered payloads get smaller. In my opinion, a good spaceplane will be closer to the size of an X-37 than our old enormous Shuttle (or maybe even smaller still).

Final point: for payloads over about 10 tons, the slope of the decreasing unit cost curve is very low. Tripling the payload capability would seem to cut the price only by a factor of 2. So, developing truly giant launch rockets, even those simplified and supported the commercial way, would not seem to pay off very well: orbital assembly from smaller payloads could be quite competitive. But, done the “government way”, such giant rockets will never compete, using the same slope on the Titan-IVB data.

Conclusions

I see no reason why we cannot build whatever craft we want, in LEO from docked modules, to perform any mission we desire, at a reasonable cost. We can do this right now.

The “breakpoint”, from a unit cost standpoint, seems to be in the vicinity of 10 metric tons delivered to LEO from Canaveral. We already have multiple launchers available in the 18-29 metric ton class, and will very soon have a 53 ton launcher. The larger, the better, for it lowers unit cost slightly.

Unless there is a specific and overriding need, I see no purpose to developing a giant launch rocket in the 100+ ton LEO payload class. I see even less sense doing this as a “government-style” operation; it would only make sense if done in the same commercial style as the existing 10+ ton Falcon-9, Atlas-V, Delta-IV, Proton, and Ariane-5 rockets. NASA has never built such a thing. Nor has any other government agency.

Falcon-Heavy will extend this to 53 tons within about 2 years, and could reasonably be expected to launch two modules at once, of up to 26.5 tons each, for its full 53 ton max payload. Another option might be 3 modules at once, of 17.66 tons each.

The rest of the existing launcher data seems to suggest that, for now, we standardize the modules of future spacecraft designs at about 14.5 to 18 metric tons, so that the maximum number of launchers will be available from the maximum number of sources. That fits very well with all current and near-term expected launchers. For example, Atlas-V-HLV could possibly carry two 14.5 ton modules.

For metric units fans:

For US units fans:

Recommended Broad Design Guidelines For Valveless Pulsejet Combustors

Update 6-5-2016:  this has to be one of the most,  if not the most,  popular article on the entire website.  Clearly there is a community out there that experiments with these things.  I hope what I posted was useful to you.
------------------------------------------------------------------

Recommended Broad Design Guidelines For Valveless Pulsejet Combustors  
GWJ       3-27-12     rev.1   4-21-12    rev.2    5-20-12
rev. 3 5-27-12 puts the appendices into a readable form
----------------------------------------------------------------------

Update 1-19-13:  This stuff was just too much fun to play with,  when I helped Justin Friend with his engines.  I must build some of these things myself.  That will require a sheet metal capability not currently in place in my shop out here on the Idea Farm.  But as soon as I do some experiments,  I will report them here on "exrocketman".  Just don't hold your breath!

Related articles also posted here include:
4-30-12      Big Student Pulsejet an Even Larger Hit at TSTC
                   big engine at TSTC
3-6-12        Student Pulsejet a Hit at EAA Meeting
                   small engine on golf cart
11-12-11     Student Pulsejet Project
                    small engine at TSTC

----------------------------------------------------------------------

(all figures and tables at end of article)         

Introduction                                

Designs for valveless pulsejets of several types have appeared on the internet as hobby devices.  These are generally based on designs that began appearing about 1909,  and which culminated about 1964,  as potential industrial or military items.  Some reports are now available on the internet,  that describe the many geometries tested long ago.  The premier examples are the folded geometries developed by Raymond Lockwood at Hiller Aircraft (ref. 1, 2),  based on French work,  and since publicized by his son.  

In this document,  the scaling proportions of the three Lockwood combustor designs are correlated versus combustion chamber size,  using the published Lockwood data.  Scaling parameters were suggested by Engebretson’s thesis (ref. 3),  in which several designs by J.W. Belter were successfully correlated for resonant proportions at one chamber size.  Chamber size as the independent variable is suggested by the fact that everything but chemistry can be scaled in some way with size.  Lockwood’s smallest test articles could only be run on acetylene-oxygen,  not propane-air,  which proves that point.  

Design details like flare geometries,  fuel injection nozzles and locations,  and starting air introduction techniques,  were not correlated.  The fundamental objective here was only a set of basic combustor tube geometries,  which might be expected to resonate well.

Scope

This document concerns itself with only the core combustor.  No ducting or augmentor devices are considered.  The Lockwood front entry single inlets are the basis of the correlation.  The relevant parameters so developed are applied to design classes resembling the side-entry Logan forms,  the multi-inlet/rear-entry Thermo-Jet forms,  and even annular reversed inlet designs.  

Not all parameters involved in the design are covered by available data,  or these correlations.  In particular,  Lockwood’s work indicated that some sort of flare on both the inlet and the exhaust helped resonance,  starting,  and performance.   However,  he gave insufficient data to correlate anything.  

Nothing in Lockwood’s documents suggests a scalable guide to how to implement those flares,  excepting a radius ratio of 22% for his HC-1 unit.  There is one comment about a 1/8-inch radius exit flare on one unit,  but no indication that other flares were attempted,  or that any flare geometries were scaled up or down in size.  

The only guidance we have in Lockwood’s documents for combustion chamber (only) length to diameter ratio is a relative constancy in the scaled proportions for the HS series.  His tailpipe taper rates appear to have been held constant as he scaled down.  

That limits correlatable scaled proportions to those describing the overall engine slenderness ratio,  the minimum tailpipe diameter ratio,  the inlet length ratio,  and the inlet to chamber size ratio (here correlated as area ratio to cover multiple or annular inlet designs).   Taper rates and chamber-only length to diameter ratios are simply recommended as constants.  

Lockwood Designs

These come from a Navy-funded program about 1959 that developed the “Pulse Reactor” (ref. 1).  That device was a combination of a very highly-rated valveless pulsejet combustor,  folded into a U-bend shape,  with venturi-type augmentor tubes on the inlet and outlet.  These devices were all about 9.1-inch chamber inside diameter in size.  With the augmentors,  maximum thrusts near 500 pounds were demonstrated,  along with minimum TSFC’s of about 1 pound per hour fuel flow per pound of thrust.  Without the augmentors,  thrusts were about factor 2.2 smaller,  and TSFC’s about factor 2.2 larger.  

Lockwood’s original “Pulse Reactor” combustor was a variation on a French design developed at SNECMA.  Hiller Aircraft and SNECMA were teamed up on this old Navy program,  and Lockwood termed his version of the basic French combustor the HS series.  The French called this folded design “Ecrevisse”,  which translates as “Crayfish”.  

In the early 1960’s,  Lockwood conducted tests of scaled-down combustors,  starting with scaled versions of the HS series.  This was an Army program,  culminating in a report published in 1964 (ref. 2).  During that effort,  Lockwood investigated two other variations:  a conical combustor geometry he designated the HC series,  and  a cylindrical combustor with a much sharper transition to the tailpipe,  that he designated the HH series.    See Figure 1.

These combustors all feature an inlet larger than the minimum size of the exhaust passage.  This is because he needed no “aerodynamic valve” effect to limit backflow out the inlet during the pressure (“spit”) phase of the cycle.  Lockwood folded his designs 180 degrees,  so that both inlet and exhaust contributed directly to total thrust.  That fold is not depicted in the figures.  This larger inlet apparently allowed the combustor to ingest far more air than the designs of others,  apparently leading to Lockwood’s devices being so very highly-rated for thrust and fuel consumption.  

It appears in the Navy report that Lockwood ran most of his 9.1 inch tests on propane.  In the Army report,  Lockwood reports that most of his scale-down work also baselined propane fuels.  There were attempts in the larger sizes to run on gasoline.  The smallest combustors would not resonate on propane-air,  but could be made to run on separate injection of oxygen and acetylene.   Lockwood gave few details on fuel injection nozzle design and location,  and essentially none on feed pressures.  

Information on the minor geometry changes to “tune-up” the resonant shell geometry was almost completely lacking.  The exceptions were one lip radius to inlet radius ratio on combustor HC-1,  the notation that a small-radius exit flare helped strengthen resonance,  and that an inlet tapered 2 degrees to converge in the efflux direction helped starting and allowed reductions in tailpipe length (the details of which he did not document in that report).  

These lacks are why the design correlations recommended here are for the gross overall combustor tube dimensions.  Details of flare radii,  fuel injection,  and starting air are not addressed in this document.  

Engebretson’s Thesis

In 1965,  Roger Engebretson published a master’s thesis at North Dakota State University on an investigation of a common class of valveless pulsejets (ref. 3).  These were developed from a series of successfully-pulsating designs by J.W. Belter.  Engebretson’s project was aimed at investigating possible propulsive application of the Belter combustors,  originally developed to be air heaters.  

Engebretson did not scale up or down in size.  He did look at 3 possible inlet tube locations,  and two inlet tube sizes.  One of the side-entry inlet locations did not work at all,  the other did,  with little performance difference between it,  and the front entry location (which was similar to Lockwood).

The main difference between Engebretson and Lockwood is that Engebretson’s inlets were rather small in proportion to the combustor diameter,  unlike the Lockwood designs.  Engebretson did this to retain the “aerodynamic valve” action of an easier “spit” out the larger exhaust passage.  As a result,  his thrust levels remained a lot smaller for the same sizes than Lockwood’s.  

Engebretson stated his TSFC’s were much higher than Lockwood’s,  but a close reading indicates he was comparing his plain-tube TSFC to Lockwood’s augmented “Pulse Reactor” devices.   Engebretson’s TSFC data are not far from those of Lockwood,  if one takes care to compare plain combustors.   Only his thrust per unit size was a lot smaller,  which this author takes as evidence of less air mass ingested through the smaller inlet,  during the intake phase of each cycle.  

In this document,  Engebretson’s data are plotted on my scaling correlations for the Lockwood data.  The sizing variables I chose were inspired by what Engebretson investigated.  I made these correlations versus combustion chamber diameter,  to reflect the fact that chemistry does not scale.  

The Engebretson combustors were simple cylindrical chambers,  with a moderate taper to a smaller straight exhaust pipe.  Engebretson never scaled up or down in size,  and he never changed the proportions of chamber versus tailpipe diameter.  See Figure 2.

Engebretson gave a little more data than Lockwood regarding the placement of fuel,  starting air,  and spark plug.  He used both gasoline and propane fuels successfully at his 4-inch size.  Further,  he notes that these same basic designs burned a mix of propane and coal dust for Belter.  Engebretson used both inlet and exhaust flares,  but gave no information about them.  

Data Correlations

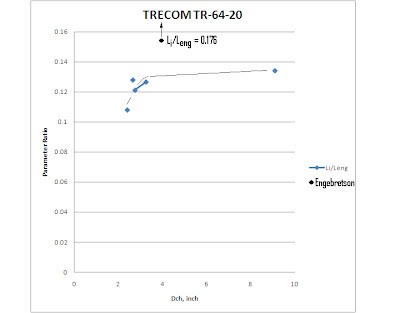
For my correlation,  I pulled data from Ref. 1 for Lockwood’s 9.1-inch diameter HS-1 tube,  and the four scaled-down configurations that Lockwood reported as “actually successful” in Ref. 2.  I put these into a Microsoft “Excel” spreadsheet (Appendix 1 attached),  and processed those data into my scaling parameters.  Some of the scaling parameters are plotted in Figure 3 below.  These include the overall engine slenderness ratio L_eng/D_ch,  the tailpipe contraction ratio as both D_min/D_ch and D_ch/D_min,  and the inlet area ratio A_i/A_ch.  These dimensional parameters are defined in Figures 1 and 2.  

It is apparent from Figure 3 that the slenderness ratio “falls off a cliff” below 3 inch chamber diameter.  This matches quite well with Lockwood’s descriptions of the difficulties he had making his smallest combustors burn at all.  This is what I believe to be the chemistry effect:  reaction rates do not scale,  while cycling rate increases.   Further,  it is easier to see the trend of tailpipe contraction expressed as D_ch/D_min than D_min/D_ch.  The scale is wrong to see the inlet area ratio trend properly.  So,  that is given in Figure 4.  Likewise,  the inlet length ratio is plotted with an appropriate scale in Figure 5.  

 

I have included on these figures the relevant Engebretson data.  Remember,  his engines were not as highly-rated,  being limited in inlet size,  and presumably limited in ingestible airflow during the “suction” phase.  

Note that in both Figures 4 and 5,  it is easy to see for all the variables the same “fall off a cliff” behavior at 3 inch diameter,  as was apparent in Figure 3 only for the slenderness ratio.  All these figures point to the same problem below a combustor diameter of 3 inches.  This is (in my opinion) chemistry and mixing unable to complete at the faster cycle times of the smaller (shorter) combustors.  

Note that Engebretson’s resonant length correlates pretty well with Lockwood’s,  as slenderness ratio in Figure 3.  We would actually expect that outcome,  whether the combustor was “highly-rated” or not,  because this exhaust length is the quarter-wave resonant length driving the pulsation cycle.  

The inlet is non-resonant,  and is “driven” by the combustor cycle.  It necessarily must be fairly short so that its inflow purges the combustion chamber and recharges it with fresh air.  Too short,  and the inlet and exhaust inflows meet too far “downstream”,  too long and these flows meet too far “upstream”.   In my opinion,  the Engebretson thesis misjudged this to be a “resonant effect”.  At about 0.13 in the figure,  the non-integer 7.5:1 length ratio is not a resonant ratio as we would normally think of it.  

What one wants is for these colliding flows to “meet in the middle” of the combustion chamber.  The fuel, air,  and the hot residual exhaust gases all mix,  thus providing ignition for the next combustion cycle.  Fuel injection style and location,  and fuel type,  critically impact this ignition process.  Many reports indicate that this can “make or break” resonant operation entirely,  no matter the geometry. 

The best “eyeball” curve fits obtained from reading these graphs are summarized in Figure 6 below.  Note the redundant equations for tailpipe contraction.  Because of the larger slope constant,  I prefer the D_ch/D_min form.   These were all formulated by reading the graph at 3 and 9 inch diameters,  assuming the evident linearity.  The reference location was 3 inches in each equation.  The basic form is the point-slope form of the linear equation in two variables.  Nothing is valid below 3 inches chamber diameter.  

Discussion of the Correlating Parameters

As defined in the figures above,  my length and diameter definitions may differ somewhat from those in the three references.  I tried to pick definitions that made sense in terms of the physical processes I know to be happening.  

In particular,  I picked the tubular length of the inlet tube as inlet length L_i,  exclusive of the axial length of any tapered bulkhead into the combustion chamber.  This is because during intake,  the sharp angle at the inlet/bulkhead joint will induce flow separation,  taking one from a transient undeveloped pipe flow,  into a chamber filled with recirculation dead zones and residual gases.  

I did include the axial length of any inlet flare in the inlet length.  This is because the intake phase uses this flare to smooth out the flow separation disturbances that a sharp tube entry would induce.  It simply is part of the length covered by the entering flow.  There is flow separation at the flare joint on the efflux phase:  that flow does not follow the curve of the flare,  at least not very much.  

The rest of the overall (straight or folded-centerline) length is the engine (resonant) length L_eng.  The forward chamber bulkhead is the pressure node for the quarter-wave resonance.  That length includes the chamber,  the axial lengths of any conical bulkheads and any tapered sections,  the entire exhaust tube,  tapered or not,  and the axial lengths of any exit flares.   I include the exit flare length in the engine length for the same fluid dynamical reasons as the inlet flare gets included in the inlet length.

Chamber diameter D_ch itself is an inside diameter (of little effect in thin sheet metal construction),  taken to be the largest diameter,  if the chamber is tapered in any way.  

There is in any of these designs at least a short length of minimal-diameter straight tube in the exhaust pipe.  This is D_min,  and it is an inside diameter.  It and the inlet size represent the two impedances to efflux massflow during the exhaust phase.  

The inlet diameter D_i associated with inlet area A_i is also an inside diameter,  and taken to be the larger diameter at chamber entry,  if there is taper.  This is more for construction dimensional control than fluid dynamics.  If the inlet tube really is tapered,  that taper is supposed to be in the efflux direction (according to Lockwood),  making the possibly-flared end of the tapered tube a little smaller.  However,  at 2 degrees taper and a relatively short length,  there is little difference in inlet diameters at either end,  even though the physically-smaller diameter is probably what controls the fluid dynamics.  

I correlated inlet size on area instead of diameter,  to allow for the possibility of a rearward-facing annular inlet geometry to replace the 180-degree fold of the Lockwood designs.  

I did not initially correlate combustion chamber length or volume.  That is a serious lack.  I do note that the combustion chamber cylindrical and taper length proportions of the Engebretson/Belter design and the Lockwood HS-series are just about the same,  and each of these is about 2 to 2.5 times the chamber diameter.  

How much of this total length is actual “combustion chamber” volume,  and how much is just a gentle entry to the exhaust tube,  is purely a matter of speculation.   The Lockwood HH-series has only a chamber length without a gentle taper,  of the same general dimensions as the cylindrical chamber of his HS series.  Lockwood’s HC-series has a straight conical chamber of roughly the same length as the combination of chamber and gentle taper in his HS series.  

Recommended Designs

 Design recommendations were formulated for three geometry classes,  to be based on these correlation equations.  The independent variable is combustion chamber inside diameter,  to be 3 inches or greater for propane.  Be very careful extrapolating beyond 9.1 inches diameter,  the results look increasingly unrealistic beyond about 10 or 12 inches.  The numerical data are appended below as Appendix 2.  

One of the three geometry classes are front-entry inlets similar to the Lockwood designs.  How to do that is illustrated in Figure 7 below,  for designs resembling Lockwood’s HS,  HH,  and HC series.  This figure shows the taper rates,  what we do know about flares,  and the best approximations I could determine for chamber lengths (as ratios to D_ch).  

The second basic geometry class is repositioning the front inlet (Lockwood type) to side inlet (Logan type) and aft inlet (Thermo-Jet type),  as shown in Figure 8 below.  The basic combustor and tailpipe is unchanged.  For side entry,  a more aft location (about 75% of cylindrical chamber length) is the one that worked for Engebretson.  For aft entry,  the inlet needs to be divided into 2 or more separate inlet tubes,  spaced circumferentially,  and preserving the total inlet area ratio.  Taper and flare do apply to each inlet separately.  

The third basic geometry is an annular aft-facing inlet,  made of a shell surrounding the basic combustor,  which has a blind end on the front.  This is shown in Figure 9 below.  The idea here is better packaging for a flight engine.  Air uptake is in the annular space,  and makes a 180-degree turn as it enters the combustor at the front end.  Inlet area ratio as correlated must be preserved in the annulus and at the front end.  The inlet length is essentially from front centerline to flare lip,  as shown,  plus a radius inward,  and must match the correlated inlet length ratio.  That last inlet length recommendation is actually very speculative,  and needs testing verification! 

What Is Not Covered

These correlations and recommendations cover the shape and proportions of valveless pulsejet tube geometries that are likely to be robustly resonant as first built,  provided that appropriate fuel injection is installed.  My best interpretation of Lockwood,  Engebretson,  and some others,  is that inappropriate fuel injection can cause an otherwise acceptable geometry to operate poorly,  or even not at all.  Further,  liquid fuels behave completely differently from gaseous fuels.  Fuel injection is necessarily a large separate topic.

The details of flare shape and sizing are poorly covered in these reports.  I could correlate almost nothing for actual recommendations.  This area needs experimentation to define the effects.  It is known that some sort of flare is beneficial,  even critical,  to tube operation.  That means the acoustical wave trap afforded by the flare on a musical instrument is having a beneficial effect on the resonant properties of the pulsejet tube.  A crude approximation (from a very old issue of Scientific American magazine)to the wave trap impedance (the “horn function”) is: 

                F(x)  =  1/[R*r]   where r is the flare radius and R is the tube radius at that same axial x

The details of starting air injection are better covered by Engebretson than Lockwood in these old reports (Ref. 1, 2,  and 3).  Even so,  there is almost no information available beyond what I put in Figure 2 above.  The feed was ordinary “shop air” at something like 85 to 100 psig.  I make no recommendations,  beyond the use of a leaf blower into the inlet,  based on what I see on the internet.  

The details of spark plug location are not well covered in any of these reports.  An educated guess says that a continuous spark source might have advantages over an intermittent device,  based on the interaction potential of the spark pulse frequency with the engine combustion cycle frequency.   No recommendations are made for that topic here.  

Some old sources point to the criticality of the timing of the fuel-air explosion relative to the “suction” phase inflow phenomena.  At full thrust in a highly-rated engine,  this suction is about half an atmosphere below ambient.  That is what drives the inflows.  

These inflows up the inlet and exhaust cause a fluid collision in the combustion chamber.  That fluid kinetic energy is converted to a small pressure rise,  thus there is a slight compression before ignition.  The explosion,  acting against the inlet and exhaust fluid columns,  is thus “confined”,  so that it produces a much higher chamber pressure.  That final pressure is about 2 atmospheres above ambient at maximum thrust in a highly-rated device.  It drives the “spit” flows out both inlet and exhaust.  

If the fuel-air explosion occurs too soon,  or too late,  pre-compression is lost,  and performance drops dramatically.  It is even possible the pulsejet will fail to operate at all.  Fuel injection velocity,  direction,  location,  and feed pressure all affect this ignition “timing”.  So does fuel type,  since there is both a physical delay,  and a demand for considerable heat,  to achieve vaporization with liquid fuels.

In his 1930-vintage“Pulse Pot” combustors,  Francois Reynst addressed this “timing” issue by means of clever fluid dynamical control.  Reynst used a guide venturi inside the combustor to force vortex formation on the blind end of his combustor.  As long as fresh air inflow persisted,  the vortex spun and grew,  but seemed not to ingest enough of the surrounding hot gases and fuel vapor to ignite.  Once inflow ceased,  the vortex continued spinning on momentum,  but the fluid flow “breakaway” (as fresh air inflow stopped) caused it to suddenly ingest large amounts of the surrounding hot gas plus fuel vapor,  leading to a sudden ignition and explosion of that vortex.  See Ref. 4.

Position of the spark source can also affect the explosion timing,  once pulsation starts.  An inappropriate spark location can cause late or early ignition” timing”,  according to some sources.  These effects can preclude operation,  or at least severely degrade performance.  

Again,  I make no recommendations regarding fuel injection details,  spark timing and location details,  or starting air details in this document.  

Addendum for Revision 1 – Thrust Intensity Scaling

To the data in Appendix 1,  I recently added some thrust scaling data.   My best estimate of actual “combustion chamber volume” would be about two chamber diameters long,  based on the Lockwood HH-series dimensions,  and on the Engebretson/Belter design.  

Using L_comb = 2*D_ch,  and thus V_comb = pi*D_ch³/2,  I computed some thrust per unit volume data vs chamber diameter.  Thrust was total for the inlet and exhaust acting together,  but with no augmentors.  These data are given in Figure 10 below.  They show little or no correlation.  

Then,  because thrust and peak cycle pressure are said to be related,  I tried thrust per unit chamber cross sectional area,  computed as pi*D_ch²/4.   These correlated very well,  as given in Figure 11 below.  The correlating equation “eyeballed” from these data,  for only diameters 3 inches and up,  is 

                F_total/A_ch lb/sq.in = (D – 3 inches)*0.35 + 1.6

Again,  this “falls off a cliff” below a chamber diameter of 3 inches,  reflecting what this author believes is insufficient reactivity of propane fuel at the fast cycle times of the higher-frequency miniature sizes. 

A similar affliction should occur with volatile liquid fuels like gasoline,  except starting at a larger diameter.  This corresponds to a longer engine length,  lower frequency,  and longer cycling time.  

Thrust Augmentation

Based on Lockwood’s work,  thrust multiplications of 1.4 to 2.2 should be possible at otherwise the same geometries and fuel flows,  given properly-designed and properly-positioned venturi-type augmentors on both inlets and exhausts.  Thrust in this sense is the sum of both inlet and exhaust,  implying a folded or reverse-inlet engine geometry.  The details of exactly how to design the augmentors is beyond scope herein.  

 

References

1. Lockwood,  Sargent,  and Beckett,  “Thrust Augmented Intermittent Jet Lift Propulsion System”,  Hiller ARD-256,  February,  1960.
2. Lockwood,  Patterson,  Beckett,  and Graber, Summary Report on Investigation of Miniature Valveless Pulsejets”, Hiller ARD-307 / Army TRECOM TR-64-20, February 1964.
3. Engebretson,  “Investigation of the Performance Characteristics of the Valveless Pulsejet”, MS Thesis,  N. Dakota State University,  February 1965.
4. Thring (ed.), “Pulsating Combustion, the Collected Works of F. H. Reynst”,  Pergamon Press,  1961.

Addendum for Revision 2 – Experimental Data (TSTC student Justin Friend)

Recent experiential data with an HS-type Lockwood combustor indicates the definite positive influence of significant inlet and exit flares of a “horn function” type of shape.  These were hose-clamped articles of slit tube bent to a constant “large” radius (more than 25% of local tube radius).  The slit gaps were filled with bent triangles of the same sheet metal,  welded in place.  

Fuel injection also proved quite critical,  even with propane gas fuel.  The final injection rig that worked was designed to stop flow at about 2 atm local pressure.  This tube included both carefully-sized outlet holes,  and a surge chamber Tee’d into the line,  fed directly from an ambient propane tank.  No reliable final dimensional data are currently available.  The near-10 inch chamber diameter HS-pattern engine failed to throttle up until the fuel injection tube matched this pattern,  however.  

This propane injection geometry was 3/8 inch OD copper tubing inserted axially into the inlet,  and clamped to one side.  It featured 4 injection holes in 2 opposed-hole pairs,  spaced about 2 inches apart axially.  These holes were in the neighborhood of 1/8 inch diameter,  which is a sensitive variable.   These holes were arranged to inject past the start of the 45 degree inlet bulkhead,  another sensitive variable.  

This large HS-pattern engine was sized with a correlation that this author did over 30 years ago.  That correlation is not the same tube geometry correlation as is recommended herein.  In particular,  the exhaust-side minimum tube diameter looks to be too large.  This difference may explain the experientially-noticed lower-than-expected thrust.   No hard measurements are available,  however.  

Figure 1 – Basic Parameters of the Three Lockwood Valveless Pulse Combustor Designs

 Figure 2 – Basic Parameters of the Belter Designs Investigated by Engebretson

 Figure 3 – Correlation Plot Usable for Slenderness and Tailpipe Contraction Ratios

 Figure 4 – Correlation Plot Usable for Inlet Area (and Tailpipe Contraction) Ratios

 Figure 5 – Correlation Plot Usable for Inlet Length Ratio

Figure 6 – Curve Fit Equations Derived from the Data Correlations

 Figure 7 – Applying the Correlations to Front-Entry (Lockwood) Designs

 Figure 8 – Extending the Correlations from Front-Entry to Side-Entry and Aft-Entry Designs

 Figure 9 – Extending the Correlations to Annular Aft-Entry Designs

 Figure 10 – Non-Correlation of Total Thrust Per Unit Combustor Volume

Figure 11 – Good Correlation of Total Thrust Per Unit Chamber Area


Appendix 1 Correlation Data - Part 1 of 3

Appendix 1 Correlation Data - Part 2 of 3

Appendix 1 Correlation Data - Part 3 of 3

Appendix 2 Estimates vs Size Based on Correlation Equations

Relationship Explains the World!

I ran across this little relationship recently:

HA   >   H

The variables are mnemonics in English for what they represent.  Literally translated,  it reads "the number of horses's asses always exceeds the number of horses".  This little relation explains so much of what I see going on around me in the world!

Quite frankly,  I'm not sure whether to call it the "Fourth Law of Thermodynamics" or the first-ever predictively-successful "Theory of Everything" in physics. 

Readers please weigh in with your comments!!!!

GW

Update 10-11-13:  This goes beyond physics.  It's actually quite useful in politics and government.

Energy Storage: Batteries vs Unpressurized Liquid Fuels

For the best batteries, source = AAAS’s “Science” vol 332 24 June 2011 p 1496. For chemical potential = 100%, there’s actual cell performance at about 50% of potential (the two-way efficiency), and ganged cells in a real battery pack at about 37% of theoretical potential, as a single overall knockdown factor. The generally available ganged-cell knowledge is really for lead-acid, but taken as “typical” for all battery types. I took the potentials in the journal article,  and knocked them all down to "deliverables" with that 37%.

For unpressurized liquid fuels, the estimate of typical actual cruising performance is based on the fuel’s theoretical heat of combustion, and about 15-20% typical overall thermal efficiency (I used 17.5%) for the hydrocarbon liquid fuels in piston engines. This does not take into account the factor 1.15 to 1.2 increase in overall efficiency observed in actual testing with ethanol at gasoline compression ratios (CR). Typically, gasoline (and ethanol) CR 7-11, diesel CR usually 20-22. Ethanol’s top CR may be in the CR 15-22 range. If so, this alone confers roughly a factor 1.5 improvement in efficiency.

I have no figures to offer for gas turbine vs piston as the IC engine component. Yet both are heat engines with similar thermodynamic source and sink temperatures. So,  the overall energy conversion efficiencies should be at least comparable. As crude as the rest of this is, piston vs turbine should not really matter.

The following table lists my best-estimate deliverable energy storage densities, in metric units, as W-hr/kg. The mass unit would be the basic battery material mass or the liquid fuel mass, not a finished production item or tank system. The “feasible now?” refers to development status. A “yes” means it is actually roadable. A “no” refers to laboratory status only. “Perhaps” is in between, but definitely not yet roadable.The added notation "(exper)" means people have actually done this,  but it is not a production item. 

Type                                           actual-cell W-hr/kg      feasible now?

Li-ion                                         300 (225 ganged)        yes

Advanced Li-ion                        600 (450 ganged)        perhaps

Li-S                                          1200 (900 ganged)       no

Zn-air                                        500 (375 ganged)         no

Al-air                                         3000 (2250 ganged)     no

Li-air                                         4200 (3150 ganged)     no

Pb-acid                                     26-34 as-ganged          yes

Gasoline/diesel IC                      2150 delivered             yes

Ethanol air IC at gasoline CR     1433 del. (2000+)        yes

Ethanol air at tested efficiencies   approx 1600-1700      yes (exper)

Ethanol air at very high CR         about 2100                  yes (exper)

A bar chart plot of these selected storage data reveals that batteries alone should be competitive with unpressurized liquid fuels if energy storage densities near 2000 W-hr/kg become roadable.  None are currently available.  Yet two are promising research items:  lithium-air and aluminum-air.  Of these,  since aluminum is more plentiful on the Earth’s surface than lithium,  I’d tentatively recommend that DOE/NREL be looking very hard at aluminum-air batteries.   It appears to be a wise R&D investment choice.

 

Now,  electric cars need not have a "super-battery" to be effective,  if the series hybrid approach is used (often called a “plug-in hybrid” today).  Most car trips are under roughly 50 miles.  An all-electric drive car need only have that much range to seem quite practical most of the time,  which reduces the battery size and cost considerably (factor 6+ reduction).  For those few trips exceeding battery range,  add a motor-generator set burning liquid fuel,  that is just big enough to keep the battery charged as you drive,  very much like the old-time diesel-electric submarines.  Surges come from the battery,  and get recharged afterward.

This approach allows one to retain all of the electric drive features already sized,  and to use a smaller internal-combustion (IC) component,  while at the same time avoiding a complicated and costly transmission to blend torque from two sources.  These characteristics all act to reduce size,  weight,  and cost,  and are a well-proven technology set long used in submarines and railroad locomotives.  These kinds of equipment have been small enough for road use since the mid-1970's. 

There is no fundamental reason why the IC component has to be a piston engine in a series hybrid.  Constant-speed turbine is a very good match to a constant-speed electric generator,  varying only torque (mixture ratio) to match load.  Gas turbine plants can easily be rigged to use any liquid fuel,  easier than a piston engine.  They are a smaller,  lighter package than an equivalent-power piston engine.  They do require a high-ratio reduction gear,  but,  that technology has existed in turboprop aircraft for 6+ decades.  

The easy flex-fuel aspect of a turbine could be very important for a variety of fuel availability reasons.  One not commonly recognized is the intermittency of fuel use in a series hybrid with a 50-mile battery-alone range.   The fuel is likely to sit in the tank for quite a while before it is used. 

Gasoline is not stable in storage for more than a few months.  Diesel is,  as is ethanol.  Ethanol–gasoline blends of significant ethanol content seem to be more stable than gasoline alone,  if the ethanol content is around 30-35%.  That’s a very “stiff” gasohol.  Kerosene is also stable in storage.  The turbine doesn’t care,  it could burn any or all of these,  separately or mixed. Diesel and kerosene are easier to refine than gasoline,  and more plentiful from a barrel of oil when refined without cracking. 

Conclusions:

1. I see no reason to disparage electric cars with batteries available right now for a commute under 50 miles.

2. A competitively long-range all-electric drive car is feasible right now,  if done as a series hybrid. 

3. The energy storage "to beat" with future batteries is about 2000 w-hr/kg, as delivered from a ganged-cell battery with realistic in-out efficiencies.

Space Travel Radiation Risks

Update 10-5-18:  I have used these data,  plus some other things since,  to revisit the radiation exposures from a Mars mission,  and how best to mitigate them.  This is a new article posted 10-5-18,  titled "Space Radiation Risks:  GCR vs SFE".  You should consider this 2012 article to be superseded by that new one one.  That new one does use exactly the same NASA data discussed here.

-------------------------------------------------------

The topic of radiation dangers and radiation shielding comes up in many on-line conversations, as well as all kinds of technical meetings associated with manned spaceflight outside of low Earth orbit (LEO). Accordingly, I went hunting on the internet and found the NASA document guiding astronaut exposure allowances, which are legally larger than for other radiation workers. Those data are summarized and posted here, as a convenient reference.

These data were copied from http://srag.jsc.nasa.gov/Publications/TM104782/techmemo.htm, titled Spaceflight Radiation Health Program at JSC (no cited reference newer than 1992). Table 1 shows the organ-specific limits, which are depth-dependent, but limited by the organ exposure at 5 cm depth in all cases. One should note that the annual 5 cm limit of 50 REM is twice that of other radiation workers here on Earth. The career limits vary by age and sex as given in their Table 2. But the max is 400 REM organ exposure at 5 cm, no matter what. I used their equations to calculate the ages at which the maximum whole-body organ exposure hits 400 REM, and added that to the presentation of their Table 2.

Galactic cosmic ray (GCR) exposures are 24 REM annual (as a slow drizzle) at solar max, 60 REM annual at solar min, pretty much a sine curve with the solar sunspot cycle ("max" = max sunspot activity when the solar wind is the strongest). Shielding for GCR is far less effective as it becomes thicker, due to secondary particle-shower effects. Note that the solar minimum exposure figure of 60 REM annual is not very far at all above the currently-allowed 50 REM annual for astronauts. Most of the solar cycle, GCR exposures are well within allowable limits.

Solar flare particles: From figure 10 reproduced below, the numbers can approach 10^4 REM during a single event, and did between Apollo 16 and Apollo 17. But, exposure is more frequently between 10^0 and 10^1 REM during more typical events, at least as they were recorded during the Apollo program. Spacecraft vs spacesuit had little effect (factor 10 at best). These are short, extremely-intense events, of several hours duration.

Solar particle shielding is described in the NASA document as “20 g/sq.cm of water-equivalent, or more”, see also fig. 9 reproduced below. That would be 20 cm of water shielding thickness, exclusive of any water tank material shielding effects.

GCR shielding data are shown in Fig 6 reproduced below, which I read at the “knee in the curve” for the diminishing returns effect. For LH2: 60 down to to 20 REM at 8 g/sq.cm, that would be 8 cm water-equivalent thickness of LH2, which is about 113 cm LH2 itself at its liquid density, exclusive of any tank wall shielding effects. For H2O: 60 down to 33 REM at 15 g/sq.cm, that would be 15 cm thickness of water, exclusive of tank wall effects. For aluminum: 60 down to 43 REM at 13 g/sq.cm water equivalent, which is about 5 cm of solid aluminum. A very nominal thickness of water essentially cuts solar minimum exposures in half.

Clearly, the most practical of those choices, from a spacecraft design standpoint, would be 15 to 20 cm of water, arranged as water and wastewater tanks surrounding the designated shelter space. That is because water and wastewater tanks will be inherent in any system capable of supporting men in space. Why not take advantage of structures you have to have, anyway?

My conclusions:

GCR is not much of a problem, as long as repeat trips are not made that exceed career limits. The 50 REM annual limit will be violated slightly at solar minimum conditions.

Solar flare particles can be shielded by creative placement of the water and wastewater tanks, tanks which will be needed anyway. I would suggest using the vehicle flight deck as the designated radiation shelter, so that critical maneuvers are not precluded by the occurrence of a solar storm.

Update 9-25-13:

This topic has come up recently as a "show-stopper" for sending men to Mars.  It is not a "show-stopper!  I did some more detailed calculations with a 2.5-year Mars mission round-trip time as baseline.  Here is what I found:

Simple fact-of-technology ----

Unless we invent better propulsion,  men-to-Mars-and-back is roughly a 2.5 year mission.

The exposure to galactic cosmic radiation (GCR) ---

Copied from http://srag.jsc.nasa.gov/Publications/TM104782/techmemo.htm,  titled Spaceflight Radiation Health Program at JSC (no cited reference newer than 1992)

Solar max GCR (not shield-able) 24 REM per year,  total for 2.5 years is 60 REM,  monthly is 2 REM

Solar min GCR (not shield-able) 60 REM per year,  total for 2.5 years is 150 REM,  monthly is 5 REM

Assumptions ---

We shall exclude the shielding effects of being on (or near in orbit to) Mars,  which cut GCR exposures to under half,  for that year out of 2.5.  Half-sky “shielding”,  reduces totaled GCR by about 20%.

We shall assume solar flares are shield-able with approximately 20 cm of water/wastewater plus the spacecraft structures,  cutting the exposure at least in half.  (Put the water and wastewater tanks around a radiation shelter area!!)  These add to the total exposure by a small percentage,  basically random in nature,  and fundamentally unpredictable in any formal sense. 

The GCR doses (annual,  total,  and monthly) listed above,  uncorrected for planetary half-sky shielding at Mars,  are thus pretty good upper estimates for the total exposure from both sources.

Astronaut rules for exposure limitations (much higher than for civilians) ----------

Copied from http://srag.jsc.nasa.gov/Publications/TM104782/techmemo.htm,  titled Spaceflight Radiation Health Program at JSC (no cited reference newer than 1992)

Male…..                150 REM.....250 REM…..325 REM…..400 REM

Female.                100 REM.....175 REM…..250 REM…..300 REM

200 + 7.5*(age-30) REM for males to a max of 400 REM maximum at calculated age 57

200 + 7.5*(age-38) REM for females to a max of 400 REM maximum at calculated age 65

Compare anticipated exposures to astronaut-rules limitations -----

No more than 25 REM in any given single month:   monthly exposure is 2 to 5 REM…………OK

No more than 50 REM in any given single year:       annual is 24-to-60 REM;  not OK at solar min,  But OK most of the cycle!!!   Consider that a 20% reduction in GCR exposure by planetary half-sky shielding at Mars,  reduces this to exactly the max limit at 50 REM,  to which any solar flare exposures must be added.  The overdose is thus actually most likely very slight,  and only occurs for missions centered at solar min,  with the lowered likelihood of some solar flare exposure!

Career exposure at solar max:  total is 60 REM;  male age 25 limit is 150 (OK),  female age 25 is 100 (OK)

Career exposure at solar min:  total is 150 REM;  male age 25 limit is 150 (OK?);  female age 25 limit 100 (not OK);  Female age 35 limit is 175 REM (OK);  calculates as 150 limit for female age 31 or 32,  note that the 20% reduction effect for half-sky shielding at or near Mars reduces this to 120 REM,  to which any random solar flare exposure must be added.  For,  say,  an assumed combined 130 REM mission exposure,  female age limits recalculate as 29 or 30.

Conclusions for Manned Mars Exploration Missions:

The only “unacceptable” danger here (under our current astronaut rules) is the annual at-most 60 REM exposure vs the max 50 REM annual limit,  at solar max conditions.  (The more probable value might be closer to 52 REM,  when half-sky shielding effects are taken into account.)  This violation may be a volunteer choice,  because it only exceeds the limit somewhat (or hardly at all),  and then only at solar max.  The “safe” interval (even without half-sky shielding effects) is some 68 or 69% of the solar cycle. 

For female astronauts,  there is a minimum age of 31 or 32 to meet worst-case career limitations,  but only if at solar max,  and ignoring half-sky shielding effects.  Male astronauts as young as age 25 meet the career limitation,  even at worst-case solar max conditions,  period.  A more likely exposure estimate actually reduces the female age limit to around age 29.

Crewmembers that fly this mission to Mars should probably not fly in space outside the Van Allen belts again,  because of those career limitations on lifetime exposure. 

While serious if the mission has to fly near solar min (max GCR radiation exposure),  this radiation danger simply does not preclude sending men to Mars with current “slowboat” propulsion.  We can do this right now!