Update 3-26-21: this third tanker study identified the best approach to refilling the lunar mission Starship on-orbit. This approach maximizes tanker operations in low circular orbit, and minimizes them to one refilled fly-along tanker sent to the elliptical departure orbit.
-------------------------------
This article presents work that follows up on the lunar
mission results already posted in Ref. 1 and Ref. 2. The first was a Spacex tanker study aimed at
refilling a lunar landing mission Starship directly in the elliptical departure
orbit required to make a lunar landing mission feasible. The second was a two-stage refilling
operation, with a full refill of the
mission Starship in low circular orbit,
and a more modest top-off in the elliptic departure orbit, from tankers sent directly there. Those orbits
were defined in Ref. 3. The
reverse-engineering of vehicle performance characteristics to support this was
presented in Ref. 4.
This
third study conducts all refilling operations but one in low circular orbit, where tanker capacities are the highest.
The mission Starship is fully refilled there, and then sent to its elliptic departure
orbit, and topped off there. All tankers are initially sent to low
circular orbit, where they fully refill
the mission Starship, and partially
refill only one tanker! That one tanker
goes with the mission Starship to the elliptic departure orbit, where it tops-off the mission vehicle before returning
to Earth directly from that orbit. This
approach got the tanker flight requirement down to only one more tanker than
would otherwise be required for a full mission Starship refill at max payload in
low circular orbit!
Orbits Considered
For clarity, the
elliptic departure orbits being considered are 300 x 7000 km altitude, and 300 x 10,000 km altitude. The low circular orbit is 300 x 300 km
altitude. Lunar missions flown from the
lower-apogee orbit can take a max 75 metric tons payload to the lunar
surface, with 0 tons payload returned to
Earth. From the higher orbit, 59 tons can be landed on the moon, with 32 tons returned. Bear in mind that these elliptic
departure orbits penetrate deeply into the Van Allen radiation belts, whose “base” is nominally about 1400 km
altitude. That definitely means
that cargo must be radiation-hard, and any
crew/passengers must have a good radiation shelter, in order to perform these lunar
missions.
Tanker Options Considered
As indicated in Ref. 1,
there are two possible tanker configurations: (1) a dedicated tanker design with extra
tankage volume in the forward spaces,
and (2) an ordinary cargo or crew Starship flow at zero payload, so that there is unused propellant aboard upon
arrival. These are based upon comments
made by Mr. Musk in his public pronouncements,
and presume the same inert vehicle mass of 120 metric tons as I
used, in reverse-engineering
Starship/Superheavy performance in Ref. 4.
Flown to the low circular orbit, and withholding only a dry-tanks landing
allowance of 9.02 tons propellant, the
deliverable-propellant capacities of these tanker options currently calculate
as 232.00 metric tons for the dedicated design,
and 192.51 tons for the ordinary Starship flown at zero payload. Those capacities are dramatically lower still, when flown to higher-energy orbits! They are max capacities: you can always fly with less, but never more!
Calculations
The refill requirements from elliptic departure for the mission
Starship were computed in Ref. 1, and
are repeated here in Figure 1 below. That
figure shows both the direct refill in elliptic, and the two-step refill and top-off
requirements. It is quite easy to see
the dramatic difference! These
refill requirements in elliptic orbit are substantially larger than the
capacities of the tanker configurations,
when flown directly to the elliptic orbits. That is exactly why the second study in Ref.
2 got the results that it did, despite doing
the initial full refill of the mission Starship in the low circular orbit.
I did simple hand calculations with a calculator to
determine the departure mass from low circular orbit for the one tanker that
accompanies the mission Starship to its elliptic departure orbit. Those are based on the top-off requirements
of the mission vehicle in the elliptic departure orbit. Those top-off requirements are shown on the
right-hand side of Figure 2, as well as
the left side of Figure 1. Note that due
allowance was made for the landing reserve propellant, while still carrying full deliverable
payload.
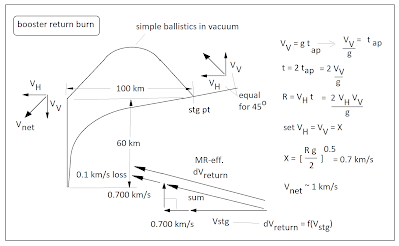
A Starship fully refilled in low circular orbit arrives in
its lunar departure elliptical orbit only a little less than full, despite it being early in the burn when you
use lots of propellant for little effect.
That is because the mass ratio MR required for the orbit-changing burn
is actually rather modest. This was
figured for 3 vacuum Raptor engines at full thrust in vacuum. That’s enough to be an impulsive burn, so the orbital mechanics delta-vee is the
mass ratio-effective delta-vee for the maneuver (factor = 1.000). Mass ratio data are given in the middle of
Figure 2, along with the propellant
loads upon arrival that allow topping off the mission Starship, while still retaining a landing reserve.
The tanker propellant loads needed in low circular orbit are
shown on the left of Figure 2. The
refill quantities are less than the propellant load by the landing
reserve. Depending upon which lunar departure
orbit and which tanker version, you add
the tanker refill quantity to the mission Starship refill quantity, to determine the total propellant that must
be delivered by tankers to low circular orbit.
The resulting procedure to run the lunar landing mission is
simple. Note that “ord” refers to an
ordinary Starship used as a tanker by flying at zero payload, and “ded” refers to a dedicated tanker design
with extra tankage capacity in the forward spaces, beyond the regular 1200 metric ton capacity.
Procedure:
Step 1. – Launch the mission Starship plus 7 ord (or 6 ded)
tankers to low circular orbit.
Step 2. – Refill the mission Starship from the first 5 ded (or
6 ord) tankers, leaving the 5th (or 6th)
with a partial load still aboard, while always
withholding landing reserve in all tankers.
Step 3. – Put that partial load in the next-to-last tanker into
the last tanker, to fill it with enough propellant
to reach the elliptical departure orbit,
plus just enough to cover the mission Starship refill, while still maintaining the tanker landing
reserve.
Step 4. – The mission Starship plus that one partly-refilled
tanker, go to the departure elliptical
orbit, while the other (empty) tankers
return to Earth using their landing reserves.
Their entry speed will be about 8 km/s.
Step 5. – The last tanker tops-off the mission Starship, there in the elliptical departure orbit, then returns to Earth using its landing
reserve. Entry speed will be about 9
km/s.
Step 6. – The mission Starship, being now fully refilled in its elliptic
departure orbit, can then carry out its lunar
nearside landing mission, including
return to a free entry at Earth, and
landing with its landing reserve. Its
entry speed will be about 11 km/s.
The tanker and refill quantity data are summarized in Table
1 below, just ahead of the figures. All are at the end of this article. How these lunar landing missions compare to
others is shown in Figure 3.
Remarks
The reader should bear in mind that these results are not
from computer trajectory or orbital simulations run on a computer! These are the results of simple hand
calculations made from simple equations,
sometimes semi-automated with a spreadsheet, and sometimes not. For such,
the use of empirical “jigger factors” is necessary to get realistic
results. Those derive from experience in
the field.
The reader should also bear in mind that the two-way mission
to a lunar landing requires significantly more delta-vee than the one-way
flight to Mars. There is potentially
propellant manufacture capability on Mars,
but not the moon. This has an
exponential effect on vehicle mass ratio.
The assumptions in common here with all the references cited
are:
#1. Vehicle “weight statement” is inert mass + payload mass
+ propellant mass = ignition mass
#2. Vehicle inert mass
presumed to be 120 metric tons,
regardless of type
#3. Engine performance factors are per Ref. 5, converted to metric
#4. Effects on performance due to throttle setting are
presumed linear, from min to max
#5. Kinematic delta-vee values are factored-up
“appropriately” to obtain mass ratio-effective values
#6. Delta vee factors are experiential judgements that
account for gravity losses, drag
losses, and any hover or divert effects
during landings
#7. For purposes of eastward launch, the surface circular velocity is used as the
kinematic velocity to attain, in order
to include potential energy effects into the rocket equation calculation
#8. For purposes of eastward launch, the surface circular velocity (or higher)
gets factored by 1.10 to account for gravity and drag losses at 5% each
#9. If launch were polar,
the eastward velocity due to Earth’s rotation at the launch latitude
would be added to the surface circular (or higher) velocity (add two rotation
velocities if westward launch)
References (all are located on this site)
#1. G. W. Johnson,
Spacex Tanker Investigation,
dated 17 March 2021.
#2. G. W. Johnson, Second
Spacex Tanker Study, dated 21 March 2021.
#3. G. W. Johnson,
Reverse-Engineering Estimates:
Starship Lunar Landings, dated 15
March 2021.
#4. G. W. Johnson, Reverse-Engineering
Starship/Superheavy 2021, dated 9 March
2021.
#5. G. W. Johnson, Reverse-Engineered
“Raptor” Engine Performance, dated 26
September 2019.
The easiest way to locate references on this site is to use the navigation tool on left-of-page. You will need the year and month it was posted, and the title. Click first on the year, then on the month. If need be, click on the title. It would be wise to scrawl all this reference date and title information onto a piece of scrap paper, before starting that research.
Table 1 – Summary of Third Study Results
Figure 1 – Mission Starship Refill Requirements
Figure 2 – Tanker Refill Requirement to Go From Circular to
Elliptic and Top-Off Mission Vehicle
Figure 3 – Comparing Lunar Missions to Other Possible
Missions