Larger vehicles tend to have higher ballistic coefficients for any given family of shapes. Hypersonic ballistic coefficient is mass divided by the product of blockage area and hypersonic drag coefficient (usually rather constant). The preferred metric units are kg for mass and square meters for blockage area. Drag coefficient is dimensionless, and depends primarily on shape in hypersonic flow. For blunt objects, hypersonic flow is Mach 3 and higher. For slender objects, hypersonic is Mach 5 and higher.
Unlike Earth, the thin atmosphere of Mars provides far less drag for braking during entry. All other parameters being equal, blunt entry vehicles of higher ballistic coefficient decelerate to about Mach 3 at lower altitudes. The experience at Mars (reference 1) has been that, for entry masses much over a metric ton, vehicles based on current technologies tend to come out of the hypersonics at altitudes too low for parachutes to provide much effective deceleration. This is compounded by terminal velocities on the chute(s) that are still supersonic. Thus, extensive final rocket braking is always required on Mars.
Any manned landings on Mars will require setting down 1-3 men (up to a ton), perhaps a couple of tons of supplies, maybe a ton or more of equipment, and around a ton for a rover “car” of some sort. This is just the “dead-head” payload. There are also the mass of the vehicle required to re-ascend to orbit, and the mass of the entry vehicle(s) that delivered all this stuff to the surface. Craft like that will weigh dozens to a few hundred tons at entry, depending upon propulsion type and vehicle layout. This is inevitable. These vehicles will have very large ballistic coefficients, and thus may actually strike the surface before the hypersonics end, at all but the very shallowest entry angles.
Landing on Mars with men is a very serious engineering problem, therefore. There are essentially only two ways around this dilemma, since even a simple minimal capsule carrying only 1 man plus landing propellant will weigh far more than a ton at entry. Those two are: (1) add extra blockage area at essentially the same mass (“inflatable heat shield”), and (2) add retro thrust during hypersonic entry to offset some of the mass, making the effective ballistic coefficient “appear lower”. One can also do both of these at once to get even more effect.
For any of these options, it is critical to understand the ballistic coefficient problem that we are trying to remedy. There is a need to estimate ballistic coefficient for very large vehicles quickly, so that “generic” studies may be performed early in the design process. Since most “back-of-the-envelope rocket equation studies” know masses better than dimensions, it is most convenient to correlate expected ballistic coefficient vs entry mass. I did exactly that herein.
Past Data
In reference 1 on page 4, table 1 contains data on every US Mars landing probe at sufficient precision to correlate ballistic coefficients. These include the two Viking landers, the Mars Pathfinder (MPF), the two MER landers (Spirit and Opportunity), and some pre-mission estimates for Phoenix and MSL (Curiosity) that are close enough for our purposes here. All of these share a 70-degree half-angle conical heat shield, with a rather squat aeroshell behind.
Here on Earth we have entry experience with ballistic warheads, the Space Shuttle, and 3 manned capsules that might resemble what we need: Mercury, Gemini, and Apollo. It is fairly easy to locate some dimensions for the heat shields for these on the internet. It is much harder to get mass at entry, especially for Gemini. Reference 2 had some very good dimensional data for Mercury, and reported a wide range of possible weights at entry that depended upon the mission duration. I used something closer to the long duration masses for purposes here. Reference 3 was unique, providing very good estimates of dimensions and masses for Gemini at entry, based on the post-entry example capsule in their passion. I got dimensions and masses for the Apollo command module from Reference 4.
The compilation of those data is given in Table 1, which is an image from a spreadsheet. Those data were in US customary units to better precision, so I converted them to metric for a better estimate of metric ballistic coefficient (beta) in the table. The Mars probe data were already metric, so I did not compute any US customary equivalents. For the old manned capsules, I obtained hypersonic drag coefficients from reference 5.
There are some differences here. The manned capsules have heat shields of a shape that is basically a spherical segment, and afterbodies of a rather tall form factor, leading to a rather large mass packed onto a smaller diameter. The exception is Apollo, which has a shorter conical shape, but is packed to a rather dense condition for its size. It was the largest and heaviest of any of the shapes. All of the Mars probes share a conical heat shield of 70 degree conical half-angle, with the point blunted. The afterbodies vary, but are all rather short for the diameters, leading to much lower masses packed onto any given diameter heat shield. I expected to see, and saw, rather scattered data.
Theoretical Grounds and Actual Correlations
All other proportions and form factors being equal, one would expect blockage area to vary with diameter squared, and volume to vary with diameter cubed. At a constant packing density, this means mass varies as diameter cubed. At constant form factor, drag coefficients would be equal. On this basis, one would expect that ballistic coefficient would correlate as proportional to diameter. That is not what happens, as is painfully evident in Figure 1.
The proportions and forms are anything but constant, and the packing densities vary even within the same form factors. Yet, bigger is both heavier and higher ballistic coefficient, generally. On that basis, there actually is a pretty good correlation of ballistic coefficient vs entry mass, which is only somewhat scattered. See Figure 2. I hoped that beta might correlate a little better as a power function of mass, and it did, as shown in Figure 3, which plots common log of metric beta vs common log of metric mass. That correlation curve fit equation is:
βpred, kg/m^2 = (374 kg/m^2)(entry mass, kg/5808 kg)^0.7752
The worth of this correlation is shown in Figures 1 and 2, where the correlation-predicted betas look pretty good vs mass in Figure 2, but are just as uncorrelated as the raw beta data vs diameter in Figure 1. The precision is poor, as are all log-log correlations. In this case, the raw data scatter about the correlation line by about a factor of 2 or 3, which is actually rather typical.
The exponent (slope on the log-log plot) corresponds to Apollo at the high end mass, and the smallest Mars probes at the low end. This may or may not overestimate the sensitivity of the beta to the entry mass, because the form factors are shorter for the probes. Yet, of the capsules, Apollo was the shortest form factor, not too unlike the probes. So my correlation may not really be that bad.
Using the Correlation
The results one gets depend upon the vehicle entry mass from whatever “back-of-the-envelope” model one is using for the Mars lander. The concept used in references 6 and 7 was a one-stage, reusable, 60 metric ton nuclear vehicle. At 60,000 kg, that vehicle would calculate as a ballistic coefficient of about 2286 kg/m^2 by the correlation. The old manned space capsules ranged from 246 to 374 kg/m^2. The Mars lander probes ranged from 64 to 115 kg/m^2.
Assuming a spherical heat shield shape, and a form factor like the Apollo, one would use an Apollo-like drag coefficient of 1.30, and calculate a diameter near 5.1 m for the 60-ton lander. Apollo calculates at an external-volume “packing density” of about 373 kg/m^3. Using the Apollo packing density, we would calculate a lander external-volume near 160 m^3. A conical shape of that volume is around 23 m tall at 5.1 m diameter, which is a much slimmer and taller form factor than Apollo. Drag coefficient for a shape like that is closer to Mercury’s 1.55 than Apollo’s 1.30, so we must iterate.
Actually, landing stability considerations on rugged ground demand that the height be much closer to the diameter. At the Apollo packing density, that 60 tons would correspond to the same 160 m^3, but at a diameter equal to the height at about 8.3 m. Using the Apollo drag coefficient, the beta calculates as 853 kg/m^2, which is factor 2.7 lower than the correlation would predict for that mass. That is within the scatter inherent in the correlation, so it is still “reasonable”.
The upshot of all this is that a reasonable exploratory beta for entry calculations might be in the neighborhood of 1000-1500 kg/m^2, for a lander in the 60 ton entry mass range. That’s good enough to get started, working on entry, deceleration, and touchdown issues. That particular mass was intended for modeling a reusable single-stage nuclear vehicle. Staged chemical designs would be in a different, larger class of entry mass. However, the same landing stability considerations apply, one way or another.
References
1. R. D. Braun and R. M. Manning, “Mars Exploration Entry, Descent, and Landing Challenges”, meeting paper downloaded from the internet, undated except no references newer than 2006.
2. Encyclopedia Astronautica article found on the internet via search keyword “Mercury capsule”, including dimensional and mass data, and a very good chronology of the entire Project Mercury effort.
3. Smithsonian exhibit article found on the internet via search keyword “Gemini capsule”, describing a recovered example of an actual Gemini capsule, in what is very close to the entry mass configuration. This is quite different from other articles, which include the retro and on-orbit service modules in their dimensions and masses, more in line with the configuration at separation from its booster.
4. Wikipedia article on the Apollo command and service modules, found via search keyword “Apollo capsule”. The data on the command module alone is very close to the entry configuration.
5. Sighard F. Hoerner, “Fluid Dynamic Drag”, section 18, figures 44 and 45. Published by the author, 1965.
6. G. W. Johnson, “Going to Mars (or anywhere else nearby) the posting version”, based on a paper given at the 14th annual Mars Society convention, in Dallas, Texas, August 2011. See the article dated 7-25-11 on http://exrocketman.blogspot.com.
7. G. W. Johnson, “Mars Mission Second Thoughts Illustrated”, a follow-up article to the convention paper in reference 6, see the article dated 9-6-11 on http://exrocketman.blogspot.com.
Table 1 – Spreadsheet Database of Dimensions, Entry Masses, and Ballistic Coefficients


Figure 1 – Ballistic Coefficient vs Diameter Does Not Correlate

Figure 2 – Ballistic Coefficient vs Entry Mass Correlates Loosely
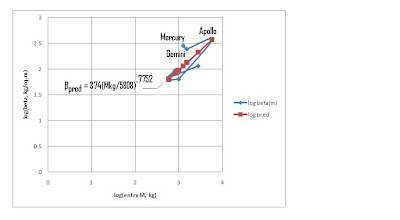
Figure 3 – Log-Log Plot of Ballistic Coefficient vs Entry Mass (Common Log Basis)
An Update: Further Analysis and Refinement (8-2-12)
The data trend through the Mars landers and the Apollo capsule under-predicts beta for the Mercury and Gemini Capsules, and so may well over-predict beta for very large objects. Accordingly, I tried a fit through just the capsule data, and fitted to the Apollo data, with an exponent of 0.2083. This trend way over-predicts beta for the landers, and so may well under-predict the beta for large vehicles. The equation and trend line are shown in Figure 3B.

Figure 3B – Modification of Figure 3 with Capsule Data Only Trend
Something intermediate was needed, so I averaged the two exponents to 0.49, and fitted it to the Apollo data as beta, kg,sq.m = 374*((M, kg)/5808)^0.49. This trend “splits the difference” fairly well between the lander probe data and the manned capsule data. All three are shown in Figure 4 for the range of masses covering the landers and the capsules. Figure 5 shows the same three trends extrapolated to very large vehicle masses, up to 300 metric tons. Of the three trends, the intermediate trend seems the most “reasonable”, but this is just a guess on my part.
In the absence of any better information, I would now scale beta vs mass using the intermediate trend equation given just above, at exponent 0.49, fitted through Apollo at 5808 kg and 374 kg/sq.m.

Figure 4 – Comparison of the Prediction Trends with Data

Figure 5 – Extrapolations with the Trends to Very Large Masses
































