The problem is not so much propulsion as it is heat
protection. The reason has to do with
the enormous energies of high speed flight,
and with steady-state and transient heat transfer. Any good rocket can push you to hypersonic
speeds in the atmosphere. But it is
unlikely that you will survive very long there!
The flow field around most supersonic and hypersonic objects
looks somewhat like that in Figure 1.
There is a bow shock caused by the object parting the oncoming air
stream. Then, the flow re-expands back to near streamline
direction along the side of the object.
Then it over-expands around the aft edge, having to experience another shock wave to
straighten-out its direction parallel to free stream again. This aft flow field usually also features a
wake zone of one size or another, as
shown.
The conditions along the lateral side of the object are not
all that far from free stream, in terms
of static pressures, flow
velocities, and air static
temperatures. One can compute skin heat
transfer using those free-stream values as values at the edge of the local
boundary layer, and be “in the ballpark”. That is what I do here, for illustrative and conceptual
purposes.
Once flow is supersonic,
the boundary layer behavior isn’t so simple any more. There is a phenomenon that derives from the
very high kinetic energies that one simply does not see in subsonic flow: energy conservation. The value of that kinetic energy shows up as
the air total temperature Tt,
which is the upper bound for how hot things could be. Air captured on board by any means
will be very close to Tt, if
subsonic relative to the airframe after capture. This includes any “cooling air” one might use!
In addition, there is
“viscous dissipation”, which has the
effect of raising the actual (thermodynamic) temperature of the air in a max
shearing zone within that boundary layer, to very high temperatures. The peak of this temperature increase is
called the recovery temperature Tr.
The difference between this recovery temperature and the local skin
temperature Ts is what drives air friction heat transfer to the
skin, not the difference between the air
static temperature and the skin temperature,
as is typical in subsonic flow.
See Figure 2. The temperature
rise from static to recovery is around 88 to 89% of the rise from static to
total, in turbulent flow, which this almost always is.
Most heat transfer calculations for this kind of flow regime
take the basic form and sequence illustrated in Figure 3. “How high and how fast” determines the
conditions of flow, ultimately. Total and recovery temperatures may be
computed from this, and total
temperature is conserved throughout the flow field around the object, regardless of the shock and expansion
processes. The flow alongside the
lateral skin is not far from free-stream to first order, and that may be used to find out “what
ballpark we are playing in”. Better
local edge-of-boundary layer estimates must come from far more sophisticated
analyses, such as computer fluid
dynamics (CFD) codes.
In Figure 3, the
process starts by determining recovery temperature. The velocity,
density, and viscosity at the
edge of the boundary layer won’t be vastly different from free stream, unless you are really hypersonic, or really blunt (detached bow shock). The various correlations account for this.
Using whatever dimension is appropriate for the selected
heat transfer correlation, one computes
Reynolds number Re. Low densities at
high altitude lead to low values, and
vice versa. High speeds lead to high
values. Different correlations have the
density and viscosity (and thermal conductivity) evaluated in different ways
and at different reference temperatures.
You simply follow the procedure for the correlation you selected. Sometimes this is neither simple, nor straightforward.
The complexity of these correlations varies. My favored lateral skin correlations use a T*
for properties evaluation that is T* = mean film plus 22% of the stagnation
rise above static. My favored slower
than reentry stagnation zone correlation evaluates fluid properties at total
conditions behind a normal shock. In the
stagnation case, Reynolds number is
based on the pre-shock freestream velocity.
The next step is the correlation for Nusselt number Nu. This nearly always takes the form of a power
function of Re (plus some other nontrivial factors), usually with an exponent in the vicinity of
0.8 or so. Nusselt number is then
converted to heat transfer coefficient h,
using the appropriate dimension and the appropriately-evaluated thermal
conductivity of the air, for the
selected correlation.
The heat transfer rate is then as given in Figure 3, which shows the Tr – Ts
temperature difference.
One should note
that because both density (which is in Re) and thermal conductivity k (which is
in h) are low at high altitudes, the
computed values of h will be substantially smaller at high altitudes in the
thin air. High speeds act to raise
h, and to very dramatically raise Tr
and Tt. That last effect is
truly exponential.
Having the heat transfer rate is only part of the
problem. One must also worry about
transient vs steady-state effects. If
the skin is completely uncooled in any way,
it is then only a heat sink of finite capacity, with the convective input from Q/Aconv
= h (Tr - Ts). One
can use material masses and specific heats to estimate the heat that is sinkable
as skin temperature rises. The highest
it can reach is Tr = Ts,
where it is fully “soaked out” to the recovery temperature. That zeroes heat transfer to the skin.
The time it takes to soak out can be very crudely
estimated as 3 “time constants”,
where one “time constant” is the heat energy absorbed to soak-out all
the way from initial Ts to Tr, divided by the initial heat transfer rate
when the skin is at the initial low Ts.
More complex steady-state situations must find the
equilibriating Ts when there is convective input from air
friction, conductive/convective heat
transfer into the interior of the object (something not illustrated here), and re-radiation from the hot skin to the
environment. In high speed entry, there is also a radiative input to the skin
from the boundary layer itself, which is
an incandescent plasma at such speeds, and
this is very significant above about 10 km/s speeds.
Not covered here in the first two estimates are heat transfer correlations
for nose tips and leading edges.
Those heat transfer coefficients tend to be about an order of magnitude
higher than the coefficients one would estimate for “typical” lateral
skin. Stagnation soak-out temperatures
should really be nearer Ttot than Tr, although those temperatures are really very
little different.
Suffice it to say here that if one flies for hours instead
of scant minutes or seconds with uncooled skins, they will soak out rather close to the
recovery temperature Tr or total temperature Ttot. That brings up practical material
temperature limits. See Figures 4
and 5.
For almost all organic composites, the matrix degrades to structural uselessness
by the time it reaches around 200 F. The
fiber might (or might not) be good for more,
but without a matrix, it is
useless. For most aluminum alloys, structural strength has degraded to under 25%
of normal by the time it reaches about 300 F,
which is why no supersonic aircraft made of aluminum flies faster than
Mach 2 to 2.3 in the stratosphere, and
slower still at sea level. Dash speeds
higher are limited to several seconds.
Carbon steels and titaniums respond to temperature very similarly, it is a very serious mistake to think that
titanium is a higher-temperature material than carbon steel! Titanium is only lighter than
steel. And you “buy” that weight savings
at the cost of far less formability potential with titanium. Both materials are pretty-much structurally
“junk” beyond about 750 F. Various
stainless alloys have max recommended use temperatures between 1200 and 1600
F. Inconel is similar to the higher end at
about 1500 F. There are a very few “superalloys”
that can be used to about 2000 F, give
or take 100 F.
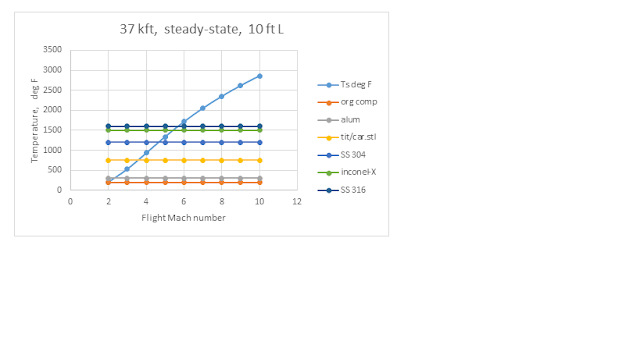
Figure 4 compares steady-state recovery (max soak-out) and
total temperatures to material limitations on a standard day at sea level. Max speed for organic composites are barely
over Mach 1, and just under Mach 2 with
aluminum. Steel and titanium are only
good to about Mach 2.5, unless cooled in
some way. Stainless steels can get you
to about Mach 3.5-to-4, the superalloys
not much higher.
Figure 4 – Compare Tt and Tr to
Material Limitations at Sea Level
Figure 5 -- Compare Tt and Tr to Material Limitations in the Stratosphere
One should note that stratospheric temperatures are only
-69.7 F from about 36,000 feet altitude to about 66,000 feet altitude. Above 66,000 feet, air temperatures rise again, to values intermediate between these two
figures! That lowers the speed
limitation some, for altitudes above
66,000 feet.
This steady-state soak-out temperature comparison neatly
explains why most ramjet missile designs (usually featuring shiny or
white-painted bare alloy stainless steel skin) have been limited to about Mach
4 in the stratosphere, and around Mach 3.3
or so at sea level. Those limitations on
speed are pretty close to the 1200 F isotherms of total or recovery
temperature. Without re-radiation
cooling, the skins soak out fairly
quickly (the leading edges and nose tips extremely quickly).
To fly faster will require cooled skins, or one-shot ablatives, or else the briefest episodes (scant seconds)
of transient flight. The
nose-tip and leading edge problem is even worse! That means for long-duration / long-range flight, the skin must be cooled, or else coated with a thick, heavy,
one-shot ablative. There
are two (and only two) ways to do cooling:
(1) backside heat removal, and
(2) re-radiation to the environment. Or
both!
Backside heat removal must address (1) conduction through
the materials, (2) some means of
removing the heat from the backside of the materials, and (3) some means of storing or disposing of
all the collected heat (what usually gets forgotten). Liquid backside cooling using the fuel comes
to mind, with the heat dumped in the
fuel tank. However, there are two very severe limits: (1) the liquid cooling materials and media
may not exceed the boiling temperature at tolerable pressures, and (2) the heat capacity of the fuel in the
tank is very finite, and decreasing
rapidly as the vehicle burns off its fuel load.
Re-radiation to the environment requires a very “black”
(highly emissive) surface coating, and
is further limited by the temperature of the environment to which the heat is
radiated. These processes follow a form
of the Stefan-Boltzmann Law, to
wit: Q/A = σ εs (Ts4
– Te4), where σ is
the Stefan-Boltzmann constant, and the εs
is spectrally-averaged material emissivity at the corresponding temperature. Subscript s refers to the hot radiating skin
panels, and subscript e refers to the
environment.
While deep space is ~4 K,
earth temperatures are nearer 300 K,
and that is what most atmospheric vehicles usually “see”. The material absorptivity is its
emissivity, which is why that value is also
used for the radiation received from the environment. A truly “black” hot metal skin might have an
emissivity near or above 0.8. This
could be achieved in some cases by a metallurgical coating or treatment, in others by a suitable black paint (usually one
of ceramic nature, and very high in
carbon content).
One More Limitation
to Consider
Once the boundary layer air is hot enough, it is no longer air, it is becoming an ionized plasma. The kinds of heat transfer calculations that
I used here become increasingly inaccurate when that happens, and other correlations developed for entry
from space need to be used instead. As a
rough rule-of-thumb, that limit is about
5000 F air temperature.
If you look at Figure 4 (sea level),
you hit the “not-air anymore” limitation starting around Mach 7. In figure 5 for coldest stratosphere, that limit gets exceeded starting around Mach
8. The only calculation methods
that “work” reliably above these limits would be CFD codes, and even then, only if the correct models and
correlations are built into the codes. That
last is not a given! “Garbage-in, garbage-out”.
That expression is no joke, it is
quite real.
With Re-Radiation
Cooling at Emissivity = 0.80
This applies only to lateral skins, not leading edges, because the heat transfer rates are an order
of magnitude higher for leading edges.
That effect alone changes the energy balance enormously.
But for lateral skins,
the speed limitation occurs when the re-radiation heat flow equals the
convective input to the skin. The
complicating factor is that convective heat transfer is a strong function of
altitude via the air density, while
re-radiation is entirely independent of altitude air density. There are now more variables at work on the
energy balance than just ambient air temperature.
That means two charts depicting the “typical” effects are
entirely inadequate. We need a sense for
how this changes with altitude air density.
What follows is a selection of equilibrium re-radiating temperature
versus speed plots, at various
altitudes, in a US 1962 Standard Day
atmosphere model. Material temperature
capabilities are superposed, as before.
Figure 11 – Lateral Skin Radiational Equilibrium at 110,000
feet
Tough Design Problem
How exactly one achieves this re-radiation cooling is quite
a difficult design problem. The skin
itself will be very hot, in order to
re-radiate effectively. Not only will it
be very structurally weak, there will be
heat leakage from it into the vehicle interior.
This is inherent, but by careful
design, can be limited to rather small (1-2%)
values compared to the energy incident and re-radiated from the outer
surface.
There must be a sufficient thickness of low density
insulation between that skin and the interior,
one capable of surviving at the skin temperature. This insulation must be some sort of mineral
fiber wool. There are no simple glasses
that survive at the temperatures of interest for hypersonic flight.
The mountings that hold the skin in place constitute
metallic conduction paths into the interior.
These must be made of serpentine shape,
of length significantly greater than the insulation thickness, in order to effectively limit heat leakage by
the metallic conduction path.
Finally, there is the
issue of sealing the structure against throughflow induced by the surface
pressure distribution relative to the pressure in the interior. Because it is much easier to design seals
that survive cold, than seals that
survive incandescently-hot, it seems
likely that the surface skins must be vented,
with the pressure distribution resisted by colder structures deeper
within the airframe.
Two Sample Cases
The SR-71 and its variants featured a “black”
titanium skin, cooled by
re-radiation, but nothing else. The leading edges (at least very locally)
would approach the soak-out temperature limits shown in Figures 4 and 5 above. Typical missions were flown at around 85,000
feet, with speeds up to, but not exceeding Mach 3.3. In the very slightly-colder air at 66,000
feet, that leading edge limit was Mach
3.5.
As figure 10 shows,
the lateral skins had a higher speed limit nearer Mach 4. So we can safely draw the rough conclusion that
the SR-71 airframe was likely limited by leading-edge heating to about Mach 3.5
or so, at something around 80,000 or
85,000 feet.
The X-15 featured skins of Inconel-X
that were radiationally very “black”. About
the max recommended material use temperature is 1500-1600 F. Leading edges might tend toward the local
soak-out limit at about Mach 4 to 4.5,
unless internally cooled by significant internal conduction toward the
lateral surfaces of a solid piece, which
these were. Thinner air “way up high”
might help with that balance, by
reducing both the stagnation, and
lateral, heating rates.
As shown in figure 11,
the re-radiation equilibrium limitation near 110,000 feet is closer to
Mach 10 for the lateral skins, and
higher still at higher altitudes, as the
other figures indicate by their trends.
The fastest flight had a white coating,
which effectively killed radiational cooling. For that,
the soak-out speed limit is closer to Mach 4.5 to 5.5, based upon figures 4 and 5.
Again, we might very crudely conclude the X-15
was limited by its leading edges to something between Mach 5 and Mach 10. The fastest flight actually flown reached
Mach 6.7, without any evident wing
leading edge or nose damage, excepting
some shock impingement heating damage in the tail section.
My Conclusions:
Most of the outfits claiming they have vehicle designs that
cruise steadily at Mach 8+ (high-hypersonic flight) have not done their thermal
protection designs yet.
That lack inherently means they do not have feasible vehicle
designs at all, since thermal protection
is the enabling item for sustained high-hypersonic flight.
“Hypersonic cruise” (meaning steady state cruise above Mach
4 or 5 for extended ranges) is therefore nothing but a buzz word, without an advanced thermal protection system
in place.
The faster the cruise speed,
the more advanced this thermal protection must be, and the more unlikely there will be a metallic solution.
Practical
Definitions:
Blunt vehicles = hypersonic Mach 3+
Sharp vehicles = hypersonic Mach 5+
Formally,
“hypersonic” is when the bow shock position relative to the vehicle
surface contour becomes insensitive to flight speed.
A Better Leading Edge
Model
That is entirely out of scope here. It might consist of one solid leading edge
piece, to be assumed isothermal. It would have a very small percentage of its
surface area calculated for stagnation heat transfer, with the remainder calculated as lateral skin
heat transfer, except as modified for
convexity into the flow near the leading edge.
There would be no conduction or convection into the interior. All surfaces would re-radiate to cool.
The next best model is a finite-element approximation, which allows for temperature variations and
internal conduction, within the leading
edge piece. Adding conduction and
convection paths into the interior is the next level of modeling fidelity. None of this is amenable to simple
hand calculation.
Supersonic Inlet
Structures
These are an even more difficult problem, as the inner surfaces are (1) blocked from
viewing the external environment for radiational cooling, and (2) are exposed to edge-of-boundary layer
conditions that are very far indeed from freestream conditions.