Protecting aircraft against missiles and ground fire is an old need. Deceiving radar with chaff goes back to World War 2, although it wasn’t originally called “chaff” then. Flares came to be, with the advent of infrared (IR) guided missiles in the mid-1950’s. Chaff and flares are the original aircraft decoys.
The problem with these is that they depart quickly behind
the aircraft, so you have to carry and
dispense a lot of them. They have gone
too far away to do any good, in about 1 second
or so at modern jet aircraft combat speeds.
And when they run out, so does
your luck, if the threats are still at
hand.
The notion of the towed decoy was originally “towed chaff”
and “towed flares”. One replaces the
many small items with just one (or a very few) somewhat-larger items that would
stay in the right place close by the aircraft,
but for a much longer time (essentially throughout the engagement and
beyond).
There are two quite-different concepts regarding the towed
radar decoy application: the towed
hardbody decoy and the towed ribbon decoy.
There is only the towed hardbody concept currently available for the
towed IR decoy application.
Towed ribbons are a different “beast” entirely, and the available radar reflection technology
only supports their use for protecting extremely low-observables aircraft. Even that application has severe
limitations. Towed ribbons are not
covered here!
Some History
The original successful towed decoy concept demonstrator was
designed by my friend Byron Hinderer at what was then Tracor Aerospace, in Austin,
Texas. He did this before I ever
reached Tracor.
That decoy featured a dorsally-attached towline (termed “cg
tow”) on a very simple body with an aft-mounted ram air turbine (RAT). The RAT supplied the electric power to make
the radar receiver and transmitter aboard the decoy function. There was no power-down-the-towline. It successfully deceived all radars in flight
tests before the Navy, despite all sorts
of “experts” saying it could not possibly work.
I spent a little over 3 years at Tracor, working on (among several other things) towed
hardbody decoys, towed ribbon
decoys, and one IR signature generation
technique that might fly aboard one of the towed hardbody decoys. This included extensive ground tests, wind
tunnel tests, and flight tests. That testing led to some very successful
flight tests of various test articles,
and a prototype design for possible acquisition by the Navy, featuring power-down-the-towline. That last became ready a year or so after I
left Tracor.
The Navy initially bought a competing design from Raytheon
instead. There were severe “teething
troubles” with tow stability initially,
because Raytheon was using an incorrect design approach: nose tow like a gunnery target, producing both an uncontrollable rolling
motion, and a cone of no protection
directly behind the aircraft. That last
reflected a decoy located behind the aircraft at its same altitude.
What really works is quite unlike towed targets: one does a “cg (center-of-gravity) tow” from
a dorsal lug, which produces a decoy tow
point that is both behind, and somewhat
below, the aircraft. The cone of no protection (where decoy and
aircraft line up in the threat’s sight picture), is thus depressed below horizontal. Thus, there
can be effective protection from a threat in a tail chase from above. Because this works so well, towed radar decoys are now common among many
countries’ armed forces.
This same hardbody tow scheme could also be used as an “airframe”
for a towed IR decoy. If airbreathing
combustion is used to produce the IR signature,
then fuel does not necessarily have to be carried on board the
decoy. It might instead come down the
towline, as an option.
Engagement Scenarios
There are some things necessary to understand about the
characteristics of engagements between threats and aircraft. The air-to-air and surface-to-air scenarios
are different, but the critical features
are grossly the same. There’s basically
head-on attacks, attacks from the
side, and tail-chase attacks.
Because the missile threats all use one or another form of
what is called “3-D proportional navigation” for their guidance, the head-on and side attack geometries have
the tendency to convert toward the tail chase scenario. How close to a tail chase these scenarios
become varies, but it does point out the
need to have decoy protection in the tail chase scenario! This is illustrated with crude sketches in Figure 1.
Figure 1 – How the Various Engagement Geometries Tend To
Convert to Tail Chases
All these engagement aspects use the same basic 3-D
proportional navigation guidance. That
guidance has built into it something termed “gee bias” that more-or-less
eliminates the downward pull of gravity as a disturbing influence on the
missile. The usual implementation
overcompensates somewhat. That has two
effects: (1) the trajectory is bowed
upward, and (2) the thinner air at the
higher peak altitude increases the missile range, to whatever extent is possible. This is also illustrated in the figure.
The basic sight picture seen by the missile is then from
somewhere behind and slightly above the aircraft. One wants significant separation between
aircraft and decoy, as viewed in that
missile sight picture! If the decoy
lines up with the aircraft, then it can
afford no protection. That is the
definitional concept behind the term “cone of no protection”. What that really means is that you want that
cone of no protection to be depressed below horizontal, as shown in Figure 2. The exception is shoulder-fired IR, which is still coming up from below as it
turns into a tail chase. Straight tow is
better for that.
Figure 2 – Threat Sight Picture and Cones of No Protection
What is shown in the figure applies directly to non-imaging
threats (radar or reticle-based IR).
Radar sees reflected energy in this or that pixel, within its narrow field of view (FOV). The seeker itself steers in such a way as to
center that “bright” pixel in its sight picture. It is the off-angle position of the seeker
(plus the range information) that allows the guidance to lead the target, to a calculated intercept point in space. If more than one pixel has reflected
energy, the seeker tends to use the
“power centroid” of the multiple “bright” pixels as its aim point at the center
of its narrow FOV.
Reticle-based IR is somewhat similar (in not forming an
image), but lacks range
information, so the estimate of the
intercept point in space is somewhat cruder.
The seeker still steers itself toward centering the power centroid of
all the hot spots it sees, in the center
of its sight picture. Seeker deflection angle
generates the information for leading the target. Like radar,
it has a very narrow FOV. There’s
just no individual pixels (which there are,
once you start using imaging IR).
Here’s the key thing for any decoy: as the missile closes upon the aircraft, its sight picture of aircraft and decoy
becomes larger and larger.
Eventually, that whole picture
cannot fit within the FOV. If the decoy
is “brighter” than the aircraft, it will
be nearer the power centroid. The more
remote aircraft then drops out of the FOV first. After that,
the only target seen by the seeker is the decoy, and the missile steers toward it rather than
the aircraft, causing the miss. Its warhead may (or may not) fuse, since the decoy is so small compared to the
aircraft that the missile designers expected.
So, two things become
clear at this point: (1) you want a lower
tow for a widest-possible sight picture, while also depressing the cone of no
protection below the line-of-sight to the descending (or at least co-altitude)
threat, and (2) the decoy’s signature
(whether radar or IR) must be “brighter” than the aircraft.
The great benefit here is that 1 decoy serves for the 1
engagement. If it is shot away, you can dispense another one, but you need not dispense multiple dozens per
engagement, the way you do with chaff
and flares. You do not need to carry anywhere
near as many towed decoys, as you do
chaff and flares, which means the
typically-larger sizes of the towed decoys are no obstacle.
What I have said about threat guidance and engagement
characteristics so far is stuff that has been in the open literature for a very
long time. I cannot say much more about
that, without getting into ITAR and
classified information. That is the
realm of counter-counter measures: the
missile guidance recognizing decoy from aircraft, and then acting upon that information.
About Towed Hardbody Decoy Design Approaches
There’s low/straight tow,
side tow, and high tow, as possible places to locate a decoy (which
moves the cone of no protection). These
are illustrated in Figure
3. Only low/straight tow
requires no automatic flight controls for stability. Having to develop the flight controls to make
side or high tow stable and reliable, is
another big development effort beyond just getting the decoy to emit
signature.
Accordingly, the
simplest, easiest, and least expensive option is to do
low/straight tow. You do want as low a
tow as possible, for enhanced stability reasons,
as well as depressing the cone of no
protection well outside the engagement sight picture. That low/straight tow is the only topic I
cover here.
Figure 3 – Possible Tow Locations and the Associated
Considerations
How This Rough-Out Design Analysis Is Done
Start with the decoy itself:
first size its tail for high “arrow stability”, then second select a trimmed-out angle of
attack that gets high downforce, and then
finally size a tow lug height for net zero-moment about the cg at your desired trim
point. Such a decoy rough-out design
results in a tow force at an angle, which
also applies as a tension to the tow cable end, and as an angle boundary condition. See Figure 4.
The details of exactly how to do this are discussed below.
Figure 4 – The Design Analysis Sequence for Roughing-Out a
Towed Hardbody Decoy
Next, you do the
curved portion of the towline. The
entire tow line is modeled as a short straight length and a much-longer curved length. For simplicity in a design rough-out, I just use a circular curved shape. The angles at its two ends are the tow cable
angle at the decoy, and zero where it
joins the straight section.
Ignoring towline weight,
the curved towline lift force must exactly balance the total decoy
downforce, and the curved towline drag
adds to the total decoy drag for the line tension where it joins the straight
section. This is an inherently
iterative process: you simply change the
length of towline in the curved section, until the vertical forces balance to zero. Exactly how to compute those forces is
described below.
The drag of the short straight section adds to the tension
applied to its end, for the tension as
felt at the aircraft. That’s the largest
tension in the towline, steady state. The size and shape of the curved portion
determine its horizontal and vertical dimensions. These plus the length of the straight section
of towline determine just how far back,
and how far below the aircraft,
the decoy is actually located.
That in turn determines the depression angle of the line-of-sight from
aircraft to decoy, which is the axis of
the cone of no protection. Accordingly, it is wise to keep the length of the straight
section short.
Recommended Towed Body Geometry
We want the decoy to fly as low as we can, to depress the cone of no protection well
below horizontal. Square or rectangular
cross sections generate more body lift at a given angle of attack than round
cross sections. So, the square cross section is the best
recommendation. Those corners can be
slightly radiused without changing that effect.
See Figure 5.
Streamline bodies generate very destabilizing moments about
their putative centers of gravity (cg),
particularly those with boat-tails or pointed rear ends. The effect is reduced a little with a bluff
rear end, which reduces the sizes of
stabilizing tail fins needed.
Hence, the bluff rear end is recommended.
In the wind tunnel,
there was a rolling instability with a cross fin pattern that was simply
not seen with an X-fin pattern. This was
thought to be related to a sort of alternating vortex shedding off the two
horizontal fins in the cross pattern.
The X-fins are always slanted,
and thus the shed vortex positions seemed to be far more stable. Hence X-fins are recommended, even if the body has to be round in cross
section for any other reason.
Putting fin trailing edges flush to the bluff rear of the
body, positions those fins farthest from
the cg, which reduces their required size
a little. Thus aft-edge-flush fins are
recommended.
Any downlift fins added to the decoy should be positioned
with their center of pressure (cp) at the decoy cg. This minimizes downlift fin moment
contributions about that cg, while
maximizing their downlift effect, which added
downlift would be the only reason for having them.
The tow lug is located axially at the cg, and on the dorsal side of the body. The towline force component parallel to the
body axis, at the lug height, is the means to trim-out the body to fly at
the desired angle of attack. Otherwise, the stabilizing tail makes it want to fly at
zero angle of attack.
The figure shows a really odd-looking recommended nose shape
for the square cross section body that is recommended. There is a good reason for that:
In the pitch plane,
the rounded nose helps delay flow separation to a point well down the ventral
surface. This maximizes the forward ventral
surface suction component of the body downlift,
which downlift we greatly desire.
In the yaw plane, the edges are
sharp, leading to flow separation on the
lee side in yaw, right at the nose. This diminishes the yaw-inducing side forces
created by lee-side suction, thus
diminishing the response to any yaw disturbances while towing.
At best, this sort of
asymmetric nose shape is difficult to do with a round body cross section. A pointed cone or ogive nose shape is pretty
much all that can be done. Such will
have equal propensities for lift and yaw forces. This is something we saw in the wind
tunnel: at the higher speeds (higher
drag/weight ratios), the round bodies
were much less stable in yaw than the square bodies with the odd nose.
The opposite was true at very low speeds (low drag/weight
ratios). But it is the higher speed
range that is of interest for jet aircraft that might need towed decoys! If you must do a round body, put a sharp cone on it, and let the flow separation induced by the
cone-cylinder joint kill the yaw forces.
That also kills body downlift forces,
so you will need to add the downlift fins to get the tow position you
desire.
That being said, on
the square body section, you put any
downlift fins at the upper chine line,
positioned axially with their ¼-chord points at the axial cg
station. Those downlift fins see cleaner
air there (remember, we are flying with
the nose pitched down, not up) and are
thus maximally effective.
On the round body,
you put them straight out from the sides at the cg. They see cleaner air there, than anywhere else.
Figure 5 – Recommended Geometry for Towed Hardbodies
About the Aerodynamic (And Other) Forces
There are the forces from the body alone, the forces from the tail fins, and the forces from any downlift fins. All of these induce moments about the decoy
cg. At zero tow force, we want that moment sum about the cg to pitch
the nose up rather strongly. That is
how we obtain “arrow stability”. Adding
in the moment of the towline force about the cg, should create zero net moment at the desired
downward angle of attack. That is how we
“trim-out” the decoy to fly the way we want it to, on that towline.
Body lift and drag are located without any moment at all, at the axial position of the body center of
pressure (cp). As indicated in the
figure above, I recommend measuring
axial position from the nose of the decoy.
This cp position is denoted as body xcp,
which varies very strongly in location. At zero angle of attack, it is typically way out in front of the
nose, for just about any imaginable
streamline body shape. As angle of
attack increases (up or down), xcp moves
quickly to some position interior to the body.
Here, positive angle of attack is
down, and positive moment acts to
increase that angle of attack.
The amount of body lift varies nonlinearly with angle of
attack, differently for each possible streamline
body shape (airship hulls, bombs, etc.).
The xcp position also varies quite nonlinearly with angle of attack, differently for various shapes. The
best thing here is to select old plotted data for an appropriate shape, and curve-fit it; which is exactly what I did.
Tail fin lift and drag forces are located at the tail
cp, which for uncambered flat plate fin
shapes, is pretty much fixed at the
¼-chord point, with a zero moment value
about that point. That means the tail
xcp is at a definite location from rear edge of the body (and thus from its
nose).
The same is true for any downlift fins, you just locate them with their ¼-chord
points at the decoy cg.
That’s three sets of lift,
drag, and cp data: body,
tail, and downlift fins. Thus there are 6 aerodynamic forces, each contributing moments about the decoy cg.
The seventh is the towline force, and the eighth is the decoy weight. These forces and locations are shown in Figure 6. For these 6 aerodynamic forces, the relevant moment arm geometry in the wind
axis coordinates uses body axis moment arms and the appropriate sine and cosine
values of the angle of attack. The
towline force component parallel to the body axis, times the lug height, is that moment, using the sum of towline angle and decoy
angle of attack. The weight acts through
the cg by definition, and thus generates
no moment.
Figure 6 – Locations and Moment Arm Data for All 8 Forces
More
About the Body Forces
An old reference had a multitude of plotted curves of the
body forces for a variety of shapes.
Among them, the square section
lift curves had roughly twice as much lift as the round section lift curves. The variation is quite nonlinear, which is why I selected a cubic polynomial
for my curve fit.
The same reference had a relatively simple model for the
body induced drag, one peculiar to streamline
bodies alone. I used that. The body zero-lift drag is just a “typical
value” one can obtain from a variety of sources, including the ones I used.
At low angle of attack,
the body cp is way out in front of the nose, and moves aft as angle of attack
increases. Bodies with bluff rear ends
showed reductions in just how far ahead of the nose the xcp is, at zero angle of attack. The correlated variation for bluff-ended
bodies was also quite nonlinear, so I
used a cubic polynomial curve fit for that,
too. All of this is illustrated
in Figure 7, with the curve fits given in Figure 8, along with the reference whose data I used.
Figure 7 – What All the Body-Only Forces Look Like
More
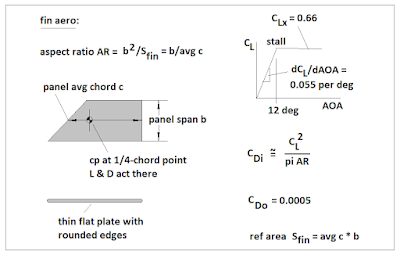
About the Fin Forces
The fin forces are easier to deal with, since the centers of pressure are essentially
fixed in location at the 1/4-chord point.
Tail fin or downlift fin, the
fundamental single-panel geometry and data are shown in Figure 9. These are simple flat plate airfoils with
rounded edges. Post-stall behavior is
simply assumed, just to have “gross
ballpark” data.
For the tail fin group,
I assumed that the leading edges could be swept, if desired.
They do not have to be. The trailing
edges I assumed straight, unswept. For the downlift fins, I presumed a constant chord, unswept.
These are to be lifting wings,
after all. All these fin designs
will behave as low, to very low, aspect ratio surfaces.
Figure 8 – Curve-Fitted Plots of the Data for Square-Section
Bodies with Bluff Rear Ends
Figure 9 – Basic Fin Aerodynamic Data
Figure 10 – How I Handled the Twin-Tail Effect of the X-Fin
Configuration
The X-fin tail is a little different than in the usual
aircraft design practice. Because of the
angles, there is a cosine component to
apply, for a panel’s projected
area. But, there is also a sort of twin-tail effect that
increases the effective area beyond just the projected area (where one side
masks the other). This opens the door to
aerodynamic interference, so I did not
double it for the twin effect, as
indicated in Figure 10. You could use a round body, but you still put X-fins on it, per the wind tunnel experience.
Towline
Aerodynamics
The towline is an essentially-cylindrical shape, which in the curved section has some local
angle of attack in every segment. The aerodynamics
came from the old indicated reference shown in Figure 11 with the data, for a cylinder in crossflow. The reference area used for the aerodynamic
coefficients in that old reference calculates as Lseg*dia, which is a sort of “planform” area for the
segment.
These are very old results,
but they are still quite useful.
The drag coefficient is simple indeed at zero angle of attack, for the lift and drag coefficients equations
shown in the figure. It is just the
additive constant in the CD equation.
I modeled the curved portion of the towline as 10 finite segments, and simply added the lift, drag,
and geometry contributions of each segment to estimate the result of the
entire curved section of the towline.
The local angle of attack at the decoy end is identical to the decoy
towline angle determined from that analysis.
It is zero where the curved section joins the straight section. Being circular, the angle at each segment is quite easy to
determine, using a constant change from
segment to segment.
I did not include the weight of the towline in my
analysis. If I were to do so, I would need data on the weight per unit
length of the towline material, and
reduce each segment’s lift by the amount of its weight, before adding everything up. Most cords are rather light, so it seemed a rather inconsequential
effect, compared to the other
assumptions being made for this design analysis.
However, that might
not be as inconsequential, if electric
power or fuel were to be delivered down the towline. That’s a change I might add to the
spreadsheet in the future.
Figure 11 – Aerodynamic Model Used For The Towline
Running Example Cases
Two things needed to be addressed. First,
a guessed drag coefficient for the zero-lift body drag was not
sufficient. Second, online research revealed that operational towed
radar decoys that did not feature large drops behind the aircraft, but did feature shapes that would actually enhance
drag.
To address the drag coefficient, I used Hoerner “drag bible” again, this time going to his chapter 3, regarding the pressure drag, skin friction drag, and base drag of a variety of shapes. The pressure drag is primarily the drag of
the nose shape. His Figure 20 offered
useful data, as sketched in Figure 12.
For the square body decoy,
I used the average of the indicated drag coefficients for the
hemispherical nose (0.01 on body cross section), and the flat-ended bluff nose (0.80). That’s a 0.405 contribution for the
nose, and using the body cross section
area reference that I wished to use.
The same figure has a nose drag coefficient of 0.20 for a
rather bluff nose, but with a small
radius transition to the basic cylinder.
I used that for 90% of the nose drag,
and 10% of the flat-ended shape (0.80) to represent the effect of the
presumed igniter for an IR decoy. That
produced a nose contribution of 0.260 for the round-body decoy.
Hoerner offers a close approximation of the Schoenherr
turbulent skin friction model that is quite easy to use, and within about a percent of the Schoenherr
value. His equation 26 from chapter 2
for that is:
1/Cfwet^0.5 = 3.46 log10(ReL)
– 4.6, where Cfwet is based
on the wetted area, and L is the wetted
length
To convert Cfwet to a cross section area
basis, one simply uses the ratio of
areas:
CfB = Cfwet Swet/Ax, where CfB is the skin drag
coefficient referenced to body cross section Ax
For the 2.5 x 2.5 inch square body decoy, the wetted length is the full decoy length of
18 inches. Evaluated at 800 ft/sec at
5000 feet altitude on a US 1962 standard day,
the Reynolds number per foot is 2.826 million per foot. Cfwet
calculates as 0.00333, and it converts
to CfB = 0.0959.
For the 3-inch diameter round-body IR decoy, the situation is much more complicated, there being a more-or-less cylindrical body
about 10 or 11 inches long, followed by
a smaller diameter blast tube to the tail,
and a final full diameter short spoiler to hold the pyrotechnic flame in
place behind the decoy. The blast tube
is largely in a base-drag wake zone,
with flow attachment around the periphery of the spoiler, behind which there is another base drag wake
zone. See Figure 13.
I used 0.9 feet for the skin drag calculation of the forward
full-diameter portion, which produced a
Cfwet of 0.00365, which
converted to a CfB of 0.0535.
I used half the body cross section as the wake zone area behind the
forward body around the blast tube, plus
the entire body cross section for the wake zone behind the spoiler. I also
treated the reattachment on the spoiler as the same blunt-but-radiused nose
drag, on half the body cross section.
According to Hoerner,
the base drag is related to the skin friction drag ahead of the wake
separation, by his equation 34 in
chapter 3:
Added CDbase (on body cross section Ax) = 0.029/CfB^0.5
For the square body,
this figured as added CDbase = 0.050, and for the base drag behind the forward body
on the round decoy, 0.1253. I use half of that for the first wake on the
theory it is about half the area, and
all of it for the spoiler wake, it being
full size. The reattachment pressure
drag on the spoiler is half that of the nose drag, that being about half the cross section.
The zero-lift body-only drag buildups are:
Item square
body round
body
Nose (pressure) drag 0.405 0.260
Skin friction 0.0959 0.0535
Fwd base drag NA 0.0627
Reattachment pressure NA 0.100
Final base drag 0.050 0.1253
Total on Ax 0.551 0.602
The zero-lift drag of the fins get added to that of the body
in the spreadsheet. That sum is the
actual estimate of the zero-lift drag of the decoy.
To address towing with or without large drop, I took a clue from the tangent of the cable
angle being the ratio of decoy total downforce (which includes its weight) to net
decoy drag (which could be reduced by its thrust, if any). I ran 1 degree AOA cases square and
round, with and without downlift, to get a min tow lug height. I also ran 6 degree AOA cases, for something halfway to fin stall. These analyses were loaded into a spreadsheet
worksheet for easy iteration. I created
separate worksheets for the square body decoy,
and for the round body decoy. The
square body setup is given in Figure 14, and the
round body in Figure 15.
Figure 12 – Nose Drag Contributions Data From Hoerner
Figure 13 – Square Body and Round Body Example Cases
Figure 14 – Square Body Setup in the Worksheet
Figure 15 – Round Body Setup in the Worksheet
It proved possible to generate decoy tow point and towline
equilibrium characterizations versus AOA with the square and round body
decoys, each with and without any
downlift fins. These data were plotted
for comparison, as shown in Figure 16 for the
square body, and Figure 17 for the
round body.
Figure 16 – Square Body Results Vs AOA
Figure 17 – Round Body Results Vs AOA
One of the surprises was the occurrence of cable angle theta
plus AOA exceeding 90 degrees for both square bodies, and with the downlifter round body. You cannot actually reach that condition in
actual tow, it is simply an artifact of
the arbitrary calculation tables used in the two spreadsheet worksheets.
From these results, I
learned that tow lug exposed heights were acceptable at small values, for the 1 degree AOA data that I had
generated. Higher AOA will require
either an inappropriately-tall tow lug,
or else we must have added aerosurfaces to produce additional nose-down
pitch moment. Not knowing what might be
appropriate as a trim angle, I used 6
degree AOA data as “about halfway to fin stall”.
I did this design analysis at a speed and altitude “typical”
of a ground attack scenario, with a high-subsonic
weapons-release constraint. Such a
constraint is actually rather typical. The
hope is that there is sufficient excess stability embodied in the tail
sizing, that the effects of higher
speeds and higher altitudes are also covered adequately, for any reasonable engagement scenario.
The risk at higher speeds is that aerodynamic forces exceed
the weight so much that the decoy no longer passively “knows” where “down”
is. The risk at higher altitudes is
that, in the thin air, inertia coupling overcomes stability, a problem well-known in high-speed jet
fighters. That is, the control accelerations afforded by the tail
fin aerodynamic forces, in comparison to
the decoy inertia, are simply too small
to effect a timely recovery from any sort of disturbance.
Ultimately, I did the
towline equilibrium calculations in the worksheets for the square body at 1 and
6 degrees AOA, with and without
downlift. And I did exactly the same
spread for the round body. The resulting
drops below the aircraft, distances
behind the aircraft, and depression
angles for the cone of no protection are all a function of total towline
length. So I ran multiple lengths for
these 8 cases, collated, and plotted the result data as depression
angle vs total towline length, for the 8
cases. Those plots are given in Figure 18. Three times a “typical aircraft length” would
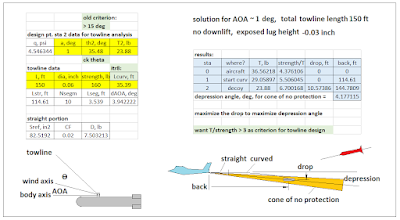
be a towline 150 feet long.
Figure 18 – Tow Positions Vs Towline Length, All Cases
This is where the design solutions become very
judgmental. For the square body at 1
degree AOA, the exposed tow lug heights
are right-at about half an inch, which
is quite realistic. Adding downlift has
more effect with a shorter towline, but
that is not very advantageous toward aircraft protection. The “right” towline length seems to be about
3 aircraft lengths, or about 150
feet, based on what little open-source
information there is on the existing towed radar decoys. At that distance, adding downlift fins depresses the cone of
protection to 5 degrees from 4, which is
not much change at all.
Adding downlift has a lot more effect at 6 degrees AOA and
150 feet: about 21 degrees vs 12. Intuition suggests we only need about 9
degrees, so we don’t need the full 6
degrees of AOA. Interpolating
linearly, it would appear the
no-downlift square body needs about 4 degrees AOA, while the downlifter square body needs about
2 degrees AOA.
For the round body,
the picture is quite similar, but
the numbers are different, because there
is less body lift available. For no
downlift, the 6 degree AOA point
generates just about 9 degrees of depression,
no interpolation necessary. For
downlift, interpolation yields an
estimated 3 degree AOA.
The net result is 4 potential decoy designs, two square body, two round body, each with and without downlift, all at 150 feet total towline length, and all targeting 9 degrees of
depression. Plus, there are two more configurations (square and
round) that tow with little depression at 1 degree AOA, and which need no downlift. That spread is:
The towline equilibria and tow position data for these 6 configurations are given in Figures 19 – 24. Bear in mind that for all trimmed AOA values exceeding about 1 degree, the exposed tow lug heights become unreasonable, requiring the decoys to be fitted with additional aerosurfaces to add down-pitch moment. That affects both total downforce and net drag, and the results have to be recomputed in response to that design change. Adding downlift reduces that trim requirement.
Now, if the decoy represents totally passive protection, you need to depress the cone of no protection well below the line of sight to the approaching threat, which should be at least co-altitude, and maybe a little above. In other words, you need the most “low” of the “low/straight tow” that you can get. That means adding downlift for the min trim aerosurface requirement, whether square or round.
But, if the decoy is not passive, then you have information about from what direction the threat approaches. In that case, you turn across the approaching threat at high gee, to prevent it from achieving a tail chase. You must know whether it approaches from the left or right, so that you can turn across it: left if on the left, right if on the right. For those scenarios, little or no depression doesn’t matter. So no added downlift or trim surfaces are required, whether square or round.
Towline strength: some of these are still marginal at best, failing the old strength/load criterion.
Figure 19 – Results for Square Body, No Downlift,
AOA 4 Degrees, Target 9 Degrees
Depression
Figure 20 – Results for Square Body, Downlift,
AOA 2 Degrees, Target 9 Degrees
Depression
Figure 21 -- Square
Body, No Downlift, AOA 1 Degree,
Target “Low Depression”
Figure 22 – Round Body,
No Downlift, AOA 6 Degrees, Target 9 Degrees Depression
Figure 23 – Round Body,
Downlift, AOA 3 Degrees, Target 9 Degrees Depression
Figure 24 – Round Body,
No Downlift, AOA 1 Degree, Target “Low Depression”
Discussion of Results
The interpolated trimmed AOA results for the round-body
decoy designs with significant trimmed AOA hit the target depression pretty
close at the selected total towline length.
The square body designs with significant trimmed AOA are in the
ballpark, but fell a bit short of the
target depression, indicating that
linear interpolation is not very appropriate.
Further iterations would be required to hit the target depression
values, and to account for the drags of
the necessary trimmed-AOA aerosurfaces.
But for illustrative purposes,
these results are close enough,
just as they are.
If depression of the cone of no protection is
important, both body shapes
benefit from adding downlift surfaces,
as these reduce either the tall tow lug requirement to trim, or they reduce the size of any added
aerosurfaces necessary to trim out the AOA.
These decoys have lower tow points behind the airplane. That would be the downlift-equipped square
body at 2 degrees, or the
downlift-equipped round body at 3 degrees.
They do fail the towline strength criterion at least somewhere along the
towline, for the presumed towline
material, which was simple nylon mason’s
twine.
If significant depression of the cone of no protection
is not deemed necessary, then
very short tow lugs, no downlift
surfaces, and no added trim aerosurfaces
become feasible. These decoys have
smaller drops behind the airplane. However, these shapes are easier to package into a
dispenser. That would be the no-downlift
square body at 1 degree, and the
no-downlift round body at 1 degree. These
do achieve about 4 degrees depression,
on the same 150 foot towline.
Both meet the old towline strength criterion with the presumed nylon
mason’s twine material.
The square body options identified here meet all of the old
criteria for stable towed decoys. Such
designs would likely require few changes in experimental development testing to
perform adequately. The round body options
identified here fail the L/D and tail volume criteria, but not by very much. But it is a risk: some changes might become very necessary
during experimental development testing.
Results are summarized in Figure 25.
Figure 25 – Results Summary
Deployment
Deployment is an entirely separate issue, as noted briefly in Figure 26. This topic was not covered
here, except in summary on that
figure. There are 2 options: slow reel and fast-braked. Slow reel could be reeled back in and
reused, but it takes long time to
deploy. Fast/braked is 1-shot
non-reusable, but can deploy very fast
at need. These are very difficult design
considerations indeed, involving large engineering
development efforts. None of those
issues were considered here.
Figure 26 – About Deployment, The Separate Issue
Final Remarks
A square body flight mechanics-only test article built to
these criteria, using these design
methods, was flight tested during 1987
at Flight Systems, at the Mojave Airport, on an F-4 “Phantom” aircraft. Flight test speeds were up to Mach 1.4, while flight test maneuvering gees were up to
6, in defensive-break maneuvers. The test pilot tried to break the tow
line, but could not. That towline was Kevlar, with very little elongation capability to
absorb line shock! That alone
demonstrates just how practical the towed hardbody decoy can be if designed
correctly! This is summarized in bullet
form in Figure 27.
Practical deployment design is an entirely separate
issue, which is its own topic. That is not covered here. The experimental test article was slowly reeled
out.
Towed ribbon decoys,
while covered by another worksheet in the same spreadsheet file, are also an entirely separate issue. Those are not covered here.
Figure 27 – Overall Conclusions
The US military is currently flying towed radar decoys. These include the AN/ALE-50 decoy for the
FA-18 and B-1B, the AN/ALE-55 fiber
optic towed decoy for the FA-18E/F (Super Hornet), and a version of the fiber optic decoy that is
being developed as the AN/ALE-70 for the F-35. Adding an IR option to the
AN/ALE-55 is also an option being considered.
The earliest one of these was the AN/ALE-50. It is the one that suffered “teething
problems”, until its manufacturer
Raytheon finally invented these same aeromechanics tow rules for
themselves. A different manufacturer (BAE
Systems) makes the AN/ALE-55 to fit the AN/ALE-50 dispenser, and is developing the AN/ALE-70, which requires a different dispenser not externally
exposed on the aircraft.
As for chaff and flares,
there is only one producer of chaff,
and two producers of flares, left
in the US. Esterline Defense
Technologies, also known as Armtec, makes both chaff and flares. It is now owned by Transdigm, which is known among some sources for
non-competitive price gouging. Kilgore
Flares company (a division of Chemring Countermeasures Company USA) also makes
flares. Chemring is in turn owned by a
company in the UK, thus being a
foreign-owned defense item source.
These are definitely business areas that could use some
competition.
Finally, I would
rather not share my towed decoy spreadsheet. However,
I might consult, using it.



























No comments:
Post a Comment