The rocket equation (as used in hand calculations) is shown in Figure 1. It inherently goes with a vehicle weight statement, also shown, in both mass and mass-fraction form. Whenever more than one weight statement applies, you may only do one rocket equation calculation for each weight statement. Velocity increments may be summed only if they occur within one weight statement!
You have a garbage-in, garbage-out (GIGO) problem with
rocket equation answers, if that weight
statement is not realistic! The
propellant mass fraction and vehicle mass ratio are utterly intrinsic to each
other, as the illustrated derivation
confirms. The calculated delta-vee (dV) capability
requirement must be sufficient to cover the required mission plus any gravity
and drag losses.
Figure 1 – Basic Rocket Equation Items
The basics for Earth launch eastward to low (about 300 km) circular
orbit at low inclination are shown in Figure 2 below. Launch is vertical, upward against gravity, but rapidly bends over in a non-lifting
thrusted gravity turn. Zeroing lift
minimizes the drag. The trajectory leaves
the sensible atmosphere at a still-modest supersonic speed, with only a slight upward angle “a” above the
local horizontal. If a two-stage-to-orbit
(TSTO) vehicle, this region is where
staging usually occurs.
For high-inclination orbits,
the dV should be increased by the eastward speed of the Earth’s rotation
at the launch site. For westward launch,
add two of those rotation speeds. Launch from other bodies is similar, except that the numbers are different, including those for the empirical fractions
from which gravity and drag losses are figured.
Ratio those Earth values, by the
ratios of the body’s surface gravity and “air” density to Earth standard values, for a first approximation.
In addition to determining dV capability from the rocket
equation, one must also size the thrust
of the engines in each stage. This is
very important, as the thrust required is
determined from the stage ignition mass,
allowing for the number of engines the stage must have. Engine mass affects the inert mass and inert
mass fraction in the weight statement!
Design iteration will be involved!
At launch, you want a
vehicle thrust/weight ratio at or above 1.5, in order not to burn so much propellant only just
above the launch pad, where speed is
still slow. Otherwise, you need to use a bigger gravity loss
fraction to figure the gravity loss you must cover with your dV
capability. Effectively, you want the net vertical acceleration above
gravity to be half a standard gee or more, to use your propellant more efficiently. This is empirical, but it has long-proven to be necessary.
Similarly, if your
vehicle is two stages, there is a
similar empirical acceleration requirement at stage 2 ignition, in order to use your propellant more
efficiently. You want half a standard
gee net above the vector component of gravity along your flight path. The simple equation is in the figure.
Figure 2 – Launch Mission Basic Items
The first figure showed how to obtain the effective exhaust
velocity Vex from the published rocket engine specific impulse Isp. Vex is what Isp would be, if it were defined in terms of
dimensionally-consistent units. It is
not: lbs of thrust divided by
lbm/sec of flow rate, and dividing-out
lb with lbm to obtain seconds, is not
dimensionally consistent! Nor is kg-f (or
metric tons-force) of thrust divided by kg/sec (or metric tons/sec) of flow
rate, and dividing-out kg-f with kg (or
metric ton-force with metric ton) to
obtain seconds! However, that tradition is too old and
well-established to change. Just deal
with it! In typical metric units, gc = 9.80667 m/s2. In US customary, it is gc = 32.174 ft/sec2.
Clearly one needs a good figure for Isp, in order to have a realistic value of Vex. The published textbook data versus propellant
combinations is crudely in the ballpark,
but not good enough for actual design! It is figured for fixed chamber pressures
that may not be the ones you want. It is
figured for fixed expansion ratios that are unlikely to be the ones you want. It is figured for 100% nozzle kinetic energy
efficiency which no real nozzle has. It
is figured for zero turbopump drive bleed gas dumped overboard, which might not be the turbopump drive cycle
in your engine. All these things affect
Isp quite strongly, except nozzle
efficiency, which is usually near 98-99%.
The best Isp estimate comes from doing the engine ballistics
yourself, per Figure 3 below. The first thing to go look up
is the data representing your desired propellant combination. That would be the chamber characteristic
velocity c*, the mixture ratio r, and the combusted gas ratio of specific heats
γ. You need a delivered c*, not a thermochemical theoretical value. The c* value and its efficiency are weak
power functions of chamber pressure, at
around 95-98% efficiency.
The second thing to quantify is the nozzle
entrance chamber pressure Pc (and pressure turndown ratio P-TDR) and dumped
bleed fraction BF corresponding to the engine and its turbopump drive cycle
that you desire to model. You need to
define max, min, and an intermediate Pc, values.
The third thing is to quantify the
characteristics of your nozzle: the throat discharge efficiency coefficient CD, the two bell half-angles a1 and a2 (if a
conical nozzle, then they are the
same, at the cone half-angle), the geometric throat area At and the geometric
exit area Ae, plus the ambient
atmospheric pressure Pa. CD
is effective throat flow area divided by geometric throat area. It is usually in the vicinity of 98-99.5%, if the profile into, through,
and beyond the throat is smooth and well-radiused. The profile radius to throat diameter ratio
should be about 1, with a short throat
flat.
The fourth thing is to do the compressible
flow nozzle analysis, which is usually
best done iteratively in a spreadsheet, the details of which are not
given here. That analysis determines the average
expansion bell half angle “a”, the
nozzle kinetic energy efficiency ηKE, and the expanded Mach number Me and pressure
ratio Pe/Pc, using the expansion area
ratio Ae/At and the specific heat ratio γ.
From those the thrust coefficient CF is determined as shown. This
includes the vacuum thrust coefficient CFvac, and the backpressure correction term, which is zero, if out in vacuum.
The fifth (and final) thing is the estimation overall
engine performance values. Thrust down
in the atmosphere is computed from chamber pressure Pc, nozzle throat area At, and the thrust coefficient CF as
shown. The relevant specific
impulse for the rocket equation must use the propellant flow rate
actually drawn from the tanks wtot. Isp can be computed either way, as shown:
from thrust and flow rate, or
from CF and c* plus a couple of other factors. For an estimate of vacuum performance, use instead CFvac as your thrust
coefficient, and figure the values with
it. In that way, sea level and vacuum performance are very
easily and quickly estimated.
Not shown in the figure is something easy to generate, if the nozzle expansion is analyzed with a
spreadsheet. By means of a standard table
of atmospheric pressure values, versus a
list of altitudes from sea level to space,
it is quite easy to obtain thrust and Isp performance versus
altitude, and even to plot it. Calculate the constant vacuum thrust and
subtract from it the varying backpressure correction term. Doing that kind of thing reliably may require
estimating the values of backpressure that cause bell flow separation! The entirely-empirical equation for that is
not in a figure, instead it is given
here:
Psep/Pc = (1.5*Pe/Pc)0.8333
That being said, optimizing a nozzle is a
separate topic in and of itself, not
shown here. Suffice it to say
that a sea level-optimized nozzle would have Pe = Pa at the nozzle design value
of Pc. There is no such thing as a “vacuum-optimized”
nozzle! There is only the max exit area
ratio that results in engines that will geometrically fit within the base volume
of the stage, allowing for
gimballing.
How to optimize Pc and nozzle expansion for best ascent-averaged Isp is
a separate topic, not illustrated here. By sacrificing some sea level thrust and
Isp, vacuum thrust and Isp can be
improved over the vacuum performance of a standard sea level design. In effect,
the nozzle is “designed” at a higher altitude than sea level, and operates over-expanded at sea level, but very definitely not so over-expanded that
it risks separation at sea level, for useful chamber pressures.
The next separate topic not shown is exactly how to estimate ascent-averaged
Isp. Some simply
arithmetically-average sea level and vacuum Isp, but that is really a lower bound, not a proper and representative average. The “right” value would have to come from a
trajectory simulation, which defeats
the purpose of simple “by-hand” estimates!
The procedure recommended here would be to compute performance versus
altitude in a table in the spreadsheet-based nozzle analysis, and simply average all the values in
the table. It’s not
“right”, but it really is fairly close.
Figure 3 – The Ballistics of Liquid Rocket Engine
Performance
The vehicle inert mass buildup is absolutely crucial to
getting a reliable weight statement,
so that the rocket equation result is also reliable. This is complicated by the fact that mass
ratio is related to mass fractions as well as masses, but you have to start somewhere. It is further complicated by the fact that
you need the propellant mass in order to estimate the inert mass of the tanks
that hold it, and you need the ignition
mass to estimate the stage thrust, from
which you estimate the inert mass of the engines that produce it. There are also interstage rings and skirts to
estimate, as well as fixed equipment
items like guidance and control hardware,
and the electrical power source that runs it. All
of this is indicated in Figure 4.
Figure 4 – Dealing With Vehicle Inert Mass Items
Usually, the analyst
is interested in delivering a certain payload mass to orbit. Guess a payload mass fraction, and a stage inert mass fraction, and compute the propellant fraction from them
as propellant fraction
= 1 – payload fraction – inert fraction. Convert the propellant fraction to mass ratio
MR as shown in the first figure above.
See if the resulting dV covers the mission
requirements; if not, adjust payload fraction (and perhaps also the
Isp) until it does. Then use
those fractions and that payload to run the actual masses in the weight
statement, and use those to estimate the
inert mass buildup, and the resulting
inert fraction. Keep iterating
until the inert fraction as used by the rocket equation agrees with the inert
fraction from directly estimating inert masses of tanks, engines,
equipment, and the various
interstages and skirts. The
payload mass and its mass fraction give you the ignition mass. That and the fractions for propellant and
inerts give you those masses. Always do
the check sums to see if you did the arithmetic right.
This weight statement convergence process is very
iterative, and the best way to do it is
with a spreadsheet. See Figure 5. You have to do two such convergence analyses
for a two-stage vehicle. The payload
mass for the first stage is the fully loaded second stage. Do the second stage first, because of that linkage, then do the first stage using that second
stage ignition mass result.
Figure 5 – Recommended Procedure to Converge the Stage Weight
Statement
There is one final aspect for sizing-out a design
concept, short of actual detailed
design. You need to estimate tank
volumes and other geometry, to estimate
a length and a diameter for the vehicle at launch. As indicated in the second figure above, this overall geometry impacts the drag loss
very significantly. This is
therefore a very important step, and a point
of further design iteration. Again, this might best be done in a spreadsheet.
Per Figure 6 below,
split your propellant mass Wp into oxidizer and fuel masses, then use their specific gravities to turn
those masses into volumes. As a
function of diameter, estimate the
tank overall lengths for the stage, and
add them. Select a number of engines to
produce the thrust. Add in a good guess
for the summed length of (1) an interstage with the G&C and power, (2) a between-tanks interstage, and (3) another good guess for the engine
overall length. That last can be modeled as
twice the expansion bell length, to
cover both the turbopump drive cycle equipment and chamber, and the gimballing engine mount. Then compute stage L/D, and select from the list the diameter that
gives the right stage L/D.
For a single-stage-to-orbit (SSTO) vehicle, this would be about stage L/D ~ 6 without the
payload, producing a still-larger, and definitely lower-drag, L/D with the payload atop the stage.
For a TSTO, do the
same procedure on the first stage, using
a desired L/D in the 3-4 range. Then make
the second stage the same diameter and find its L/D. Sum the L/D’s for the two stages
together: you will again want about 6 for
the two stages together, without the
payload.
Figure 6 – Running the Geometry from the Weight Statement
You will have already needed to set a number of engines for
each stage, and to re-scale their dimensions
from the ballistics analysis thrust level to the as-sized thrust level. Dimensions scale proportional to the square root of
thrust.
Once the vehicle is sized,
check to make sure your engines will actually fit the bases of the
stages. You may need to revise vacuum
engine expansion ratio to change the exit diameter and bell length. Or perhaps change the number of engines (and
rescale them). Or both.
The result of doing all of this correctly is the roughed-out
sizing of a credible launch vehicle concept,
and good ballpark estimates of its performance and payload
capability. Such is now ready for you to
invest in actual detailed design and analysis,
especially if it is the best concept you have evaluated, among several competing concepts.
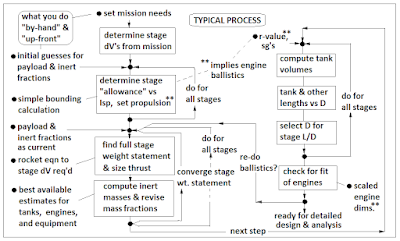
Doing this “up-front” stuff by-hand (assisted by
spreadsheets) is the way to reduce the cost of evaluating multiple concepts
inexpensively and quickly enough, to
permit raising the odds of success, by
using true brainstorming to generate multiple concepts. See Figure 7, which applies to all sorts of engineering
development efforts, not just sizing
launch vehicles.
Figure 7 – General Development Process That Includes
Brainstorming Cost-Effectively
Where to Obtain the Spreadsheet Tools
There are three general-application spreadsheet tools that
support doing this kind of analysis. There
is a fourth spreadsheet tool that is not general, but is useful for making oversimplified
bounding calculations, for Earth launch
SSTO and TSTO concepts. See Figure 8.
Figure 8 – Available Spreadsheet Tools and Supporting
Materials
The first general tool is a 2-body elliptic
orbits calculator that can be used to determine the theoretical velocity
requirements of space missions. Its
results must be tempered with some empirical estimates for losses, in order to determine the mass
ratio-effective delta-vee (dV) numbers.
Those loss estimates and that orbit analysis are not covered here.
Another general tool is a rocket engine
performance calculator in which the propellant combination is modeled with a
specific heat ratio γ, a chamber c*
velocity as a function of chamber pressure,
and an oxidizer/fuel mass flow ratio “r” that is also a function of
chamber pressure. The nozzle is modeled
with half-angles for its kinetic energy efficiency, and a throat area massflow discharge
coefficient (or area efficiency). The
nozzle expansion conditions and thrust coefficient are sized from an appropriate
chamber pressure level, and either
a design expanded pressure, or a
design expansion area ratio. The engine
cycle is modeled by the throttleable range of chamber pressures, and the dumped-bleed fraction of turbopump
drive gases.
The third general tool is a reentry dynamics
and stagnation convective heating calculator that is based on the simple model
used by H. Julian Allen for warhead entry back in the 1950’s. To it,
I have added a stagnation plasma radiation heating estimate. The atmosphere is modeled by a “scale height”
type of simple exponential model for density versus altitude, and an altitude at which “entry interface”
begins at orbital-class speeds. The
entry conditions are speed and path angle at entry interface. The entering object is modeled by its
hypersonic ballistic coefficient and (only for heating) the effective value of
its “nose tip” radius.
The oversimplified rocket vehicle sizing tool for
bounding calculations presumes that there is only one weight statement
involved, so that all the dV values may
be summed into a simple calculation for each stage. It does include the sizing of stage thrust
values, which impacts inert masses, and it does estimate tankage volumes, which also impact inert masses. This is done in a way that allows the user to
force clean, low-drag shapes, of adequate but not excessive slenderness
ratio. But it is also only a bounding
calculation, a good start-point for
more investigative design. The numbers
are indicative, but not really
trustworthy.
These tools are available as free downloads by way of the
Mars Society’s “New Mars” forums, as
indicated in Figure 9 below. Those
same postings also offer a whole series of course materials as free
downloads, that teach the user how to do
these various things, in greater
detail.
For the four spreadsheet tools discussed here, the links from the New Mars forums postings
are reproduced here:
Item name (link below)
2-body orbits spreadsheet orbit basics.xlsx https://www.dropbox.com/scl/fi/cxtpsx2ne7ltg77syavxt/orbit-basics-spreadsheet.xlsx?rlkey=w6g4p5et7yacnxrwls5inmkmv&dl=0
Rocket performance spreadsheet liquid rockets.xlsx
Rocket user manual document user man.pdf
Results reporting image engine sizing
report.png
Entry spreadsheet entry
estimates.xlsx
Entry user manual document user manual revised entry.pdf
Oversimplified rocket vehicle
sizing tool launch sizing.xlsx
User Manual part 1 of 3 user
manual launch sizing.pdf
User manual part 2 of 3 addendum
to user manual.pdf
User manual part 3 of 3 addendum2.pdf
Figure 9 – Where to Find Links to the Tools on the New Mars
Forums
How to Do the Initial Bounding Analysis for SSTO
One can get a crude approximation to get started, by doing a rather simple bounding calculation
with the rocket equation. The vehicle
sizing / bounding calculation spreadsheet tool can be used for this. The numbers are not trustworthy for
design, but they are indicative. Figure 10 shows the sort of inputs
that you need. LOX is liquid
oxygen. LH2 is liquid hydrogen. LCH4 is liquid methane. RP1 is rocket-grade kerosene.
Figure 10 – Data Sources for the SSTO Bounding Analysis
The rocket equation-in-reverse is used to determine the
propellant mass fraction, and from that
the “allowance” that you have for the sum of inerts and payload. Results are given in Figure 11.
Where the allowance curve is above the inerts-only
band, there is the possibility of
carrying payload. The bands for
inerts-only fractions in the plot at lower right are based on miscellaneous
modern stages for the expendables,
Falcon cores for the reusable first stages that enter at low speeds, and good educated guesses for fully reusable
items capable of orbital entry and some sort of landing.
Note that reusable first stage cores do not apply for SSTO
bounding purposes, as they are not
orbital entry-capable. They tend to hit
atmosphere at only about Mach 3, whereas
full orbital entry hits atmosphere at about Mach 25. The entry heating is vastly different!
The figure shows a spreadsheet image and 3 plots made from
it, annotated appropriately. Required mass ratio MR is shown versus
propulsion specific impulse Isp, which
is what most people look at, but is the
least informative. There is a plot of
both propellant mass fraction Wp/Wig and the “allowance” for the sum of inert
and payload fractions, but the scale is
inconvenient. The most informative plot
is only “allowance” versus Isp in the lower right, where bands of inert fraction Winert/Wig at
zero payload fraction Wpay/Wig can be spotted upon it, as well as bands of possible Isp versus
propellant combination. That is the most
useful for bounding calculation purposes.
Figure 11 – Results for Initial SSTO Bounding Calculation
What we actually see from the lower-right plot is that an
expendable SSTO can be propelled with any of the 3 propellant combinations
investigated. However the payload
fraction potential with LOX-RP1 is essentially nil, and with LOX-LCH4 it is very small (on the
order of only 1-2%). With LOX-LH2, expendable SSTO payload fraction potential is
significant (on the order of 4-7%).
It is very unlikely that the inert fraction of a reusable
SSTO powered by LOX-LH2 could ever be as low as 10%, but if it were, the payload potential might be on the order
of 1%, and that only with the highest-possible
engine performance.
It is far more likely that the inert fraction of a reusable
LOX-LH2 SSTO would fall in the range of 15-20% (or even more, depending upon how the landing is to be done, and whether it is a lifting body or has wings), which falls above the required allowance
curve! That very clearly precludes
the possibility of successful reusable SSTO design even with LOX-LH2 propulsion,
and even at zero payload fraction! Such
a design would need something significantly better than chemical rocket
propulsion as we know it today (required Isp in the 500-1000 sec range, or more).
Details: More About Doing Engine Ballistics
The liquid rockets.xlsx spreadsheet does liquid rocket
engine chamber ballistics (from propellant and cycle information) and
expansion nozzle compressible flow analysis (to include both sizing the
expansion, and calculating resulting
performance). Results from both topics
combine to produce the engine specific impulse values.
The propellant information includes models for c* and r
versus chamber pressure Pc, where that
is at the entrance to the nozzle,
downstream all of the engine cycle features and components. The pressure feeding-in to those features from
the pumps can be, and most often
is, substantially higher! Chamber ballistics is primarily determining
the throat area and nozzle propellant flow rate to meet a thrust requirement at
a certain Pc. The throat area discharge
coefficient CD is a real-world efficiency factor that is part of the
nozzle flow determination.
There is no need to model all the details of the engine
cycle that drives the turbopumps. This
usually involves hot gas taps,
preburners, and/or stages of
combustion at off-design mixture ratios.
All we need to know to estimate engine specific impulse Isp is
the fraction of massflow dumped overboard (BF) relative to the massflow drawn
from tankage. The sum of nozzle massflow
and dumped massflow equals the massflow drawn from tankage.
The nozzle is a converging-diverging channel for which the
diverging portion usually has one conical half-angle near the throat, and another smaller one at the exit. These two angles are used to estimate rather
closely the kinetic energy efficiency ηKE of the nozzle, a real world efficiency factor that helps
determine thrust coefficient accurately.
It represents the exit area average of the cosine component factors of all
the exiting streamline velocity vectors.
The effects of fluid friction are essentially zero compared to this
streamline divergence effect, which is exactly
why propulsion nozzle expansions can be modeled quite well with isentropic
compressible flow models.
The thrust coefficient provides a very convenient way to directly
relate thrust to chamber pressure, and
to hardware size (in the form of geometric throat area). It is composed of a vacuum thrust
coefficient, less a backpressure
correction term. The vacuum
thrust coefficient depends only upon the expansion geometry Ae/At and kinetic
energy efficiency ηKE. The
backpressure correction term depends upon the expansion geometry Ae/At, the chamber pressure Pc, and the ambient atmospheric pressure Pa. It is zero,
out in vacuum where Pa = 0 by definition.
Vehicle performance depends upon the thrust, and vehicle mass depends upon the propellant
drawn from the tankage. So for the
rocket equation model to apply, the engine
specific impulse must be based upon the massflow drawn from tankage, not just the nozzle massflow, which is smaller if BF is not zero. In such cases,
specific impulse is higher if computed with the nozzle-only
massflow, something often reported for
marketing-hype purposes! But using it
leads to incorrect answers in rocket equation vehicle performance estimates!
This picture is represented conceptually in Figure 12.
Figure 12 – How Liquid Engine Ballistic and Performance
Estimates Are Done
The solid rocket has quite different engine
ballistics from the liquid, so the
liquid engines.xlsx spreadsheet is entirely inappropriate for calculating their
estimates! Only the nozzle sizing
and performance calculations are identical,
which deceives many newcomers to this field. To analyze vehicles powered by solid
rockets, you need a reliable specific
impulse value, but how you get it is
entirely different from the way you get it for a liquid.
The solid has exactly the same nozzle massflow equation for
a given chamber pressure, which in
steady operation must exactly match the massflow coming off the burning surface
of the propellant grain (a term for the propellant charge). That burning surface can vary during the
burn, sometimes drastically. But the main quandary is that the propellant
burn rate is a power function of chamber pressure (for no erosive
burning)! A lesser complicating factor
is that the chamber c* velocity used in the nozzle massflow equation is also a
weak power function of chamber pressure.
For no erosive burning,
there is a balance of the nozzle and propellant grain massflows, with chamber pressure appearing in 3
places, distributed on both sides of the
steady balance equation. (This gets to
be transcendental with erosive burning,
making the direct solution for Pc impossible.)
Solving this balance for the chamber pressure reveals an
exponential sensitivity of equilibrium pressure to variations in any of the
factors in the equation. The higher the
burn rate exponent, the more sensitive
this balance is. Also, the motor blows up anytime the sum of burn
rate exponent and c* exponent equals or exceeds 1! See Figure 13.
Figure 13 – The Ballistic Balance in a Solid Rocket Motor
The basic message here is that you need a solid rocket
analysis code or spreadsheet to properly determine the sizing and performance
of a solid motor. An introduction to
what that really looks like is given in the “exrocketman” article “Solid Rocket
Analysis”, posted 16 February 2020. (That site is http://exrocketman.blogspot.com.) One can quickly navigate to the article
using the archive tool left side of page.
Click on the year, then the
month, then the title if need be. In this case,
there is no need to click on the title,
the article was the last thing posted that month, top-of-list.
This is a very large topic and article! Note that with solids, there is no bleed fraction BF and there is no
pressure turndown ratio P-TDR;
plus, the oxidizer/fuel mixture
ratio r is meaningless.
The hybrid rocket has quite different engine
ballistics from both the liquid and the solid,
so the liquid engines.xlsx spreadsheet is entirely inappropriate for
calculating their estimates! The
regression rate for an unoxidized fuel looks like the erosive burn rate
correlations for solid propellants. For
an under-oxidized fuel, it has both the
exponential pressure dependence term, and the erosive burning term, for a two-term regression correlation in 2
different variables.
Only the nozzle sizing and performance calculations are
identical, which again deceives many
newcomers to this field. To analyze
vehicles powered by hybrid rockets, you
need a reliable specific impulse value,
but how you get it is entirely different, and is not discussed here at all. Apparently,
only numerical simulations really work at all.
Details: Analyzing and Optimizing Conventional Fixed-Bell Nozzles
Nozzle sizing and performance for rocket engines is best
done with the compressible flow model,
at no gain in entropy (“isentropic flow”), albeit with empirical corrections for the
effective throat area in terms of massflow (discharge coefficient CD), and with empirical corrections for streamline
divergence effects at the exit area (nozzle kinetic energy efficiency ηKE). That is how one obtains a reliable figure for
the actually-achieved estimated value of thrust.
For sizing, there is
(1) the expansion area ratio Ae/At and its effects upon expanded Mach number Me
and pressure ratio (Pe/Pc or Pc/Pe), and
(2) the effects of hardware size (embodied as throat geometric area At) upon
design thrust F at some design chamber pressure Pc.
Figure 14 – Calculating Sizing and Performance of Nozzles
It is possible to determine the expanded Mach number Me from
the design value of the expanded pressure ratio, in a closed-form solution, using Pc/Pe = [1 + (γ – 1) Me2/2]γ/(γ
– 1). The easiest way to do this is
to convert the pressure ratio to a temperature ratio Tc/Te = (Pc/Pe)(γ –
1)/γ = [1 + (γ – 1) Me2/2].
Then solve the temperature ratio equation for the Mach number: Me =
[2*(Tc/Te – 1)/(γ – 1)]0.5 . The
expansion area ratio can then be calculated with that Mach number from the
compressible streamtube area ratio equation:
Ae/At = (1/Me)[2*(Tc/Te)/(γ + 1)]0.5(γ + 1)/(γ – 1). These
are the standard isentropic relations.
It is not possible to determine the expanded Mach
number directly from the area ratio as a closed form solution. The compressible streamtube area ratio
equation is transcendental in Mach number,
so that solution is inherently iterative. That is where software or a spreadsheet can
be used with great labor savings. Once
that Mach number is known, it is used in
the pressure ratio equation to determine the exit expanded pressure.
“Sea level-optimized” designs are generally perfectly
expanded (Pe = Pa) at sea level, for the
design value of the chamber pressure.
That might (or might not) be the max value the engine is capable
of, but it will be close, something like 80+% of max. These designs then have the lowest area expansion
ratios Ae/At, and the least vacuum
thrust (where the exhaust is inherently underexpanded, to that least expansion ratio).
There is no such thing as a “vacuum-optimized”
nozzle design! Such a thing
would have an infinite expansion ratio (and dimensions) in order to reach a
zero expanded pressure from any finite chamber pressure! In the real world, there is some finite space at the rear of the
stage, into which some appropriate number
of “vacuum engines” must actually fit. That
fit behind the stage is what limits the area expansion ratio.
The limitations are both the stage diameter and the length
of the space into which these engines must go,
and how that fit is determined also depends on the number of engines
selected, allowing for gimballing some,
but perhaps not all, of the
engines. Ultimately, this is driven by the thrust required at
stage ignition, the stage diameter to
meet fineness ratio requirements, and
the length available between that stage’s aft tank bulkhead and the top of the
lower stage.
My point:
vehicle design requirements determine allowable vacuum engine
expansion ratio, not the engine expansion
sizing alone. “Vacuum” engines have
larger expansion ratios, and better
thrust in vacuum, at the same flow rate
and chamber pressure, than their sea
level counterparts. But in general, they cannot be fired in the open air at sea
level, due to flow separation in the
bell that is induced by too much ambient atmospheric backpressure! Such separation leads to destruction the bell
in a matter of seconds, due to localized
overheating at the location where the shockdown occurs inside the bell.
These sea level and vacuum designs are the endpoints
of a possible spectrum of designs that could serve as “ascent engines”
between sea level and vacuum (outside the sensible atmosphere). Such ascent engines could be operated at sea
level near (or at) full chamber pressure,
with near-incipient separation,
resulting in an expansion ratio intermediate between the optimized sea
level and vacuum designs. If operated at
sea level at low chamber pressure,
separation ensues! Sea level
thrust is less than that of a true sea level design, because the exhaust is overexpanded, and suffers a very large backpressure
correction term on thrust. But performance
going out into vacuum is much better than a sea level design, while not quite as good as a “real” vacuum
design.
See Figure 15 for typical results, calculated for engines all sized to the same
chamber pressure and massflow rate (different bells fitted to the same power
head and throat area). The baseline
powerhead was the sea level engine.
Thrust level for sizing was set such that the same throat diameter and
total flow rate was obtained for all 3 engine designs. The 10 metric ton-force thrust class was
simply chosen arbitrarily. Rescale it at
need. Dimensions vary with square root
of thrust. Flow rates vary with
thrust. Isp does not rescale.
Figure 15 – Comparison of Sea Level, Ascent,
and Vacuum Designs
Bear in mind that there are multiple detailed choices for
the various parameters, so that the
final answers obtained are not always the same as these initial rough estimates, although they are always rather close to what
is depicted here. I sized the sea level
and ascent designs at max chamber pressure for this study.
80% max Pc might have been a better choice, especially for a higher-technology design at
higher max Pc. It is easier to ignite
and quickly ramp up to something like 80% power, than it is to ignite and quickly ramp up all
the way to full power. Full power starts
have been a “no-no” for many decades now,
starting with the engines in Von Braun’s V-2 rockets.
Regardless, the trend
is clear regarding good ascent engines for first stages and SSTO designs: you sacrifice a little thrust and Isp at sea
level for much better thrust and Isp out in vacuum, compared to a real sea level design. The vacuum performance of the ascent engine
design is still less than the performance of the “real” vacuum design, but it is a lot closer than the sea level
design ever could be. The
ascent-averaged Isp of the ascent design is rather close to its vacuum
level, and not all that far from the Isp
of the typical fit-limited “real” vacuum design.
Case Study:
All-Expendable SSTO
The overall bounding study indicated that only the LOX-LH2
expendable SSTO looks to be competitive with an all-expendable TSTO. Accordingly,
I came up with a modest-technology LOX-LH2 ascent engine sizing to
support such a design traceably, using
the “r noz alt mod” worksheet in the “liquid rockets.xlsx” spreadsheet. See Figure 16. I then used the “launch sizing.xlsx”
spreadsheet’s “SSTO exp” and “tank sizing” worksheets to size a vehicle of the
correct fineness ratio, complete with a total
thrust specification at liftoff. See
Figure 17.
Figure 16 – Engine Sizing Report for LOX-LH2 Ascent Engines
of Modest Technology
Figure 17 – Vehicle Sizing For an Expendable LOX-LH2 SSTO
Case Study:
All-Expendable TSTO
The overall bounding study indicated that the upper stage of
an all-expendable TSTO should be powered with modest-technology vacuum LOX-LH2
engines, while the lower stage could be
powered by either modest-technology LOX-LCH4 or LOX-RP1 ascent engines. I chose RP1 to get the benefit of the higher
fuel density.
Accordingly, I came
up with a modest-technology LOX-RP1 ascent engine sizing to support such a
design traceably, using the “r noz alt
mod” worksheet in the “liquid rockets.xlsx” spreadsheet. See Figure 18. I used the same tool to size a modest
technology LOX-LH2 vacuum engine. See Figure
19. I then used the “launch
sizing.xlsx” spreadsheet’s “TSTO exp” and “tank sizing” worksheets to size a
vehicle of the correct fineness ratio,
complete with a total thrust specification at liftoff, and at second stage ignition. See Figure 20.
Figure 18 – Engine Sizing Report for Modest-Technology
LOX-RP-1 Ascent Engine
Figure 19 – Engine Sizing Report for Modest-Technology
LOX-LH2 Vacuum Engine
Figure 20 – Vehicle Sizing Report for an Expendable
LOX-RP1/LOX-LH2 TSTO
Case Study: Feasibility of Reusable SSTO?
I used the “SSTO reU” worksheet in the “launch sizing.xlsx”
spreadsheet to investigate the possibility of a reusable SSTO, as a lifting body entry craft in order to
minimize its likely inert mass fraction.
Lifting body craft will have landing speeds in the 300 mph class. True winged craft will have landing speeds in
the 200 mph class, but also higher inert
mass fractions, to support wings
extended in near-broadside hypersonic flow without them being ripped off. The
worksheet has a means to crudely estimate what those inert mass fractions might
be. Strictly speaking, it is limited to the high engine
thrust/weight ratios of chemical engines,
especially in smaller vehicle sizes.
The first configuration estimated used the same
modest-technology LOX-LH2 ascent engine sizing that was used for the expendable
SSTO. Those results show clear infeasibility, as the leftover payload fraction is
negative, as indicated in Figure 21.
The second configuration in Figure 22 is the same
lifting body, just with the
ascent-averaged Isp raised (by about 27 sec) to represent a higher-technology LOX-LH2
engine. It still shows as infeasible, and by an amount comparable to the
modest-technology option. A little more
Isp (maybe 10 s) might be available, but
that clearly will not help.
The third configuration simply raises the ascent-averaged
Isp to a value more-or-less representative of what was achieved by the old
NERVA nuclear thermal rocket engine technology,
circa 1974. This shows to be
feasible, and at an attractive payload
mass fraction, although this performance
is likely over-estimated, since the low
thrust/weight ratio of the solid core nuclear engine is not correctly
modeled in the inert mass buildup options!
See Figure 23 for the (rather unreliable) numbers. They really only indicate some level of
feasibility, but not really by how much!
Bear in mind that the NERVA exhaust was radioactive, so this kind of nuclear technology is not
something you would really want to use in a reusable SSTO! However,
the Isp modeling this, is in a
class not approachable with any available chemical rocket technologies known
today! And THAT is the real
message here!
Figure 21 – Bounding Calculation for Modest-Technology
LOX-LH2 Reusable SSTO: Infeasible
Figure 22 – Bounding Calculation for High-Technology LOX-LH2
Reusable SSTO Still Infeasible
Figure 23 – Bounding Calculation for NERVA-Based Nuclear
Reusable SSTO: Feasible
About the “Orbits+” Courses:
This document details the how-to that corresponds to certain
lessons in the “orbits+” course set,
that is available for free download via the Mars Society’s “New Mars”
forums. Those lessons on vehicle
sizing, engine performance
estimation, and launch (specifically
from Earth) correspond to what is discussed here. This document presumes the reader is already
familiar enough with orbital mechanics to know how to estimate the velocity
requirements, that are factored-up to
cover losses. If not, the first few lessons in the course set, cover that topic.
By-hand analysis techniques still have a useful role to play
in all sorts of engineering disciplines,
not just space launch as is covered here. The models are simple, they have few inputs, and they do not require that a real design
with proper drawings has already begun.
The results are less precise, but
they are good enough to tell a good idea from a bad one. See Figure 24.
What that makes possible is two-fold: (1) you can quickly and cheaply screen a lot
of brainstormed ideas up-front, enabling
you to commit the significant resources of starting a real design, to only the best one or two ideas, and (2) if you can obtain approximate by-hand
estimates, you can better recognize
garbage-in/garbage-out problems with the computer-generated results of the full-blown
design process. Those two possibilities
can save you a ton of grief and money, over the long run.
Figure 24 – Where By-Hand Estimates Fit Into the “Big
Picture”
Where most people get into this launch stuff is by asking
the question “how big a rocket do I need to get to my desired
destination?” The answer is usually
obtainable with the classical rocket equation,
but only if you know how to use it properly! It needs the correct inputs for engine
performance and velocity requirements,
and the correct weight statement inputs to represent the various stages
or vehicles. These inputs in part are
theoretical (orbital mechanics), and in
part are quite empirical (loss factors, inert
mass buildups, etc.). The different topics (among those needed)
can lead the student to entirely-different destinations in terms of
skills, as shown in Figure 25.
Figure 25 – Where Most People Start: Asking Questions About Rockets
I laid out a series of course lessons aimed at bringing the
novice up-to-speed quickly and efficiently,
based on no math more difficult than high school algebra. Classical orbital mechanics requires multiple
presentation lessons to get the basics of the physics and how things interact
across to the student, before the
student is ready to attempt solving problems with it. This is indicated in Figure 26 as
lessons 1-3 for the presentations, and
lesson 3B as the corresponding problem-solving session.
There is a spreadsheet tool that makes running the 2-body
orbit numbers far easier in the 3B problem session. The problems start with solved demo problems
to show the student exactly how to do this,
then proceed to similar assigned problems for the student to work. The solutions to the assigned problems are
provided, in order for the student to self-assess
how well he/she did.
Launch is a more empirical topic, complete with ways to estimate what are
called gravity and drag losses. Those
losses have to add to the velocity requirements that size the vehicle. This is
covered in lesson 4, with 4B as the
problem-solving session.
The problem of interplanetary transfers is covered for
min-energy Hohmann transfers in lessons 5 and 5B, and for faster transfers in lessons 5.5 and
5.5B. There are both theoretical orbital
mechanics and some empirical real-world effects that are parts of these lessons
(such as mid-course correction budgets). The lessons suffixed with B’s are the
problem sessions.
Lessons 6 and 6B cover the basics of the entry, descent,
and landing problem, to include
some very empirical real-world items necessary for doing any of this. The more detailed ability of estimating entry
dynamics and heating is covered in lessons 7 and 7B, supported by a spreadsheet adaptation of the
old by-hand estimates made in the mid-1950’s for warhead entry, updated.
Lessons 8 and 8B cover the basics of doing custom
spreadsheets to link multiple rocket equation burn analyses and weight
statements together, in order to
determine estimated vehicle performance (the topic of this article. There is an oversimplified spreadsheet tool
available for bounding calculations, but
the student will, by this time, need to do his own custom spreadsheets, with multiple rocket equation analyses linked
together and done in correct order.
Lessons 9 and 9B cover how to create reliable estimates of
liquid rocket engine performance from few inputs. The engine “cycle” that drives the turbopumps
is not addressed, except that its dumped
gas bleed fraction is needed to get a reliable specific impulse figure. Scope is limited to fixed expansion
bells, and some appropriate empirical
factors are included.
Figure 26 – What Are The “Orbits+” Course Offerings
All the course topic areas are covered in the same way, as indicated in Figure 27. There is one or more “present the basics”
lessons that resemble lectures, followed
by one (or more) problem-solving sessions.
These include working a demo for the students, followed by assigning similar problems to the
students. Solutions to the student
problems are provided for self-check on how well the student did. Each lesson
has a course text document, and an
associated slide set for teaching it to others,
plus supporting spreadsheets and user manuals as needed. As indicated in
Figure 28, the course materials
can be obtained via links posted on the Mars Society’s New Mars forums. Direct links to the supporting spreadsheets
are located just ahead of Figure 9 above.
Figure 27 – How the Courses Are Structured
Figure 28 – Where Most of the Course Materials Can Be
Downloaded For Free
Final Comments
I first did this kind of rocket equation thing for a living,
as a graduate student while taking a
summer off, to work at what was then LTV
Aerospace’s Marshall Street Facility,
working in the “Scout” launcher group.
I sized 1-off configurations and advanced launcher designs, plus I helped with orbital analysis for
customer satellite launches. I did
exactly these kinds of hand calculations in order to set up design models of what
I wanted to “fly” with LTV’s “NEMAR” launch trajectory code.
This sort of by-hand analysis to set up real design efforts
was exactly what I did working for Rocketdyne/Hercules in McGregor, Texas,
once I left graduate school. I
did this for both rockets and ramjets,
particularly the booster rockets for the ramjets. Once again,
this sort of thing sets up the actual design efforts, the exploratory testing, and the planning of what to pursue next.
I did some of this same by-hand work at what was then Tracor
Aerospace in Austin, Texas, between two tours at the McGregor rocket
plant. I did this kind of thing for both propulsive decoy items, and for towed decoy items (a different subject
not involving the rocket equation).
Again, it helped screen candidate
ideas in a cost-effective fashion, it
helped set up real design efforts, it
helped determine exploratory testing,
and it helped guide the planning.
I (and all the colleagues around me) started out doing this
sort of thing pencil-and-paper, running
numbers with a slide rule, most of the
time. Only occasionally, when there was no other way, we would run a software code model on the
computer, which in those days was an
enormous power-consumptive mainframe, which
you communicated with by batch runs of punch cards in a steel tray, and waited hours before your results ever came
back.
We quickly converted to scientific calculators, but it was still literally pencil-and-paper
work. Desktop computers were still years
in the future, and spreadsheet software
years after that. But since those
times, I have maintained my abilities to
do by-hand engineering design analysis,
assisted now by both calculators and modern spreadsheet software. The spreadsheets offer a fast way to iterate
solutions, and to plot your data.
To see what the old style tools once were, see Figure 29. Some of you may not know what a slide rule
is! It did what today’s calculators
do, for about 300 years before there was
any such thing as a calculator.
Other than that, I
would invite interested persons to visit the New Mars forums site for more than
just the free downloads of the stuff I have put together on this rocket vehicle
sizing subject. Poke around, and see all the various things forums
participants have discussed. Such might
be of considerable interest to you.
Consider also becoming a member and participating. To do so,
contact newmarsmember@gmail.com.
Figure 29 – Old Style Engineering Tools, Circa 1960’s and 1970’s





























No comments:
Post a Comment