According to Wikipedia,
Spacex’s “Raptor” as it will power the “Starship” upper stage spacecraft
is a staged combustion cycle such that gas bled to power the pumps is
reintroduced (no overboard dump).
The max chamber pressure as intended for the design is reported
by Wikipedia to be just about 4400 psia.
It reportedly has an area ratio of 40,
although a vacuum-only design might be nearer 100. The reported design value for sea level
thrust (at the area ratio of 40) is 440,000 lb.
Wikipedia lists performance as 330 sec Isp at sea level and
380 sec in vacuum. I am doubtful of that
last figure, unless the longer vacuum
expansion bell is used.
Wikipedia lists its “diameter” as 1.3 meters (about 51
inches); I presume this is exit area at
the 40:1 ratio. I also presume it will
have just about 5:1 pressure turndown ratio.
It uses liquid oxygen and liquid methane as its
propellants. I have good models for
r-factor and c* for this propellant combination. A good default for gas specific heat ratio is
1.20. A good default for the expansion
bell is an average half angle of 15 degrees.
I ran my “liquidrockets.xlsx” spreadsheet tool to
reverse-engineer the performance of this engine, using the new “allin1des” worksheet that does
nozzle CF and engine sizing ballistics,
plus altitude performance estimates,
all in one place.
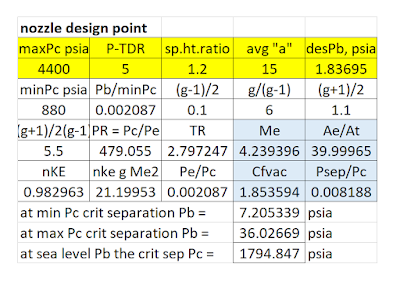
Sizing the nozzle proportions was slightly iterative, in that I had to iteratively determine the
perfect-expansion design backpressure such the expansion ratio matched the 40:1
figure reported in Wikipedia. The worksheet
output image for this group is given in Figure 1.
Figure 1 – Image of Nozzle Design Group
Doing the ballistics to size the engine was also
iterative. I used a chamber/throat area
contraction ratio of 5, and a chamber L*
= 90 inches for this. I also presumed
the nozzle throat discharge efficiency was 0.995. It was values of the vacuum thrust level that
I had to input iteratively, until I
achieved the 440,000 lb sea level thrust that Wikipedia reports. This group’s image is given in Figure 2.
Figure 2 – Image of Ballistics and Sizing Group
This gave me the data necessary to estimate performance vs
altitude (from sea level to vacuum) for both max chamber pressure = 4400 psia
(per Wikipedia) and min chamber pressure = 880 psia, calculated from the max value and my presumed
5:1 pressure turndown ratio. This groups
image is given in Figure 3. Note the
54.4-inch exit diameter in my model,
which is not far at all from the 51 inch value quoted by Wikipedia.
Figure 3 – Image of Performance vs Altitude Group
The critical backpressure values for onset of nozzle flow
separation in the expansion bell are given in Figure 1. They show that there is no danger of flow
separation when operating at max chamber pressure, from sea level to vacuum. When operating at min chamber pressure, the nozzle will be separated somewhere just
below 20 kft, at local ambient
atmospheric pressure 7.2 psia. The min
allowable chamber pressure at sea level that does not flow separate is
estimated at 1795 psia, which
corresponds to a min allowable turndown ratio on the launch pad of 2.45, instead of the max turndown ratio of 5
presumed otherwise.
Plots of thrust coefficient CF, thrust F,
and specific impulse Isp, all vs
altitude, are given in Figures 4, 5, and
6, respectively. All these show the expected behaviors. Thrust is reduced from its vacuum value by
the exit area times ambient backpressure term.
That term zeroes as you climb into vacuum.
Figure 4 – CF vs Altitude at Max and Min Pc
Note the full-pressure level of specific impulse at sea
level: calculated to be 334.4 sec vs
Wikipedia’s 330 sec. My
spreadsheet-estimated performance is thus very close to the public claims for
this engine. The difference is out in
vacuum: my spreadsheet estimates full
pressure vacuum performance as 360.4 sec,
not the 380 sec claimed in the Wikipedia article. That higher value would have to correspond to
the longer vacuum bell, not the 40:1
bell that can be used at sea level, with
at least some turndown.
This spreadsheet can estimate performance at altitude, but it does not calculate the dynamical
flight performance of an ascending rocket vehicle. It would take such a real trajectory program
to find out what the effective average Isp might be, for flight from sea level to vacuum.
That being said, just
arithmetically-averaging the values in the spreadsheet table (in Figure 3) will
get one “into the ballpark” for realistic use in the rocket equation. My spreadsheet shows a full-pressure average
of nearly 355.4 sec.
Be aware that this model indicates you cannot successfully
operate this engine below about 20 kft altitude at the min chamber
pressure. From there on up, the full 5:1 pressure turndown (to only 880
psia) is available without risking flow separation. But,
at lower chamber pressures, the
backpressure term is proportionally larger in effect, and the chamber c* velocity is a little
lower. Down low in the atmosphere, low-pressure Isp values are substantially
lower than full-pressure Isp values (at 20 kft,
295.2 vs 348.5 sec). The difference
is small out in vacuum, but still not
zero: 353.8 sec vs 360.4 sec.
“Starship”, as
currently envisioned, has 7 of these
40:1 “Raptor” engines, totaling at sea
level some 3,080,000 lb of thrust at liftoff at full power setting. Projected values from Musk’s presentations
seem to indicate an inert mass of 85 metric tons, a payload near 100 metric tons, and a max propellant load of 1100 metric
tons. That totals to some 1285 metric
tons at liftoff. If the payload is
nearer 200 tons, the liftoff mass is
nearer 1385 tons. For a figure-of
merit, call it a nominal 1300 metric
tons.
1300 metric tons is 1,300,000 kg. On Earth this mass weighs some 12,749,000
N. Converting this to US customary lb at
1 lb = 4.447 N, we get a weight (for
“Starship” without its booster) to be lifted of 2,867,000 lb. This is a takeoff thrust/weight at max
throttle setting of 1.074. That’s barely
adequate, but in line with some other
heavy vehicle designs. It should be
possible to flight test this vehicle single-stage, without the booster, even if fully loaded. Whether it can reach orbit is another matter.
I ran a quick rocket equation investigation (using another
spreadsheet) of “Starship” using these reverse-engineered performance
results. I used the claimed 85 metric
ton inert mass and 1100 metric ton propellant mass, and a zero payload mass. I used 7.9 km/s orbital velocity, factored up 10% to account for best-guessed
5% losses each for gravity and drag. I
ignored the deorbit burn, and presumed a
low-altitude terminal velocity to be “killed” of 0.5 Mach, factored-up by 1.5.
The results say that the “Starship” alone (no booster) can
barely reach orbit, with no
payload. That would be its single-stage-to-orbit
(SSTO) potential. The key here is
whether the 85 ton inert weight can be achieved in a vehicle capable of
surviving reentry, and still be capable
of a propulsive landing, as
claimed. But if those numbers remain
realistic after the initial suborbital flight tests, then, yes, it
has SSTO potential: “Starship” alone can
likely reach low Earth orbit unladen,
for flight test purposes.
That spreadsheet image is given in Figure 7.
Figure 7 – Rocket-Equation Estimate of Unladen “Starship”
Alone to Orbit
Update 6-28-19: I did a quick re-analysis of the “Raptor”
with a larger expansion bell such that the bell expansion exit area ratio was
200, not 40, and keeping the same throat diameter and
total flowrate as the sea level design.
This gave me a vacuum thrust near 501,700 lb per engine, at essentially the same throat area and total
flow rate.
Vacuum specific impulse computes as 381 sec, versus the 380 reported on the Wikipedia
website. That’s really rather close! Close enough to trust my reverse-engineering
analysis. Sea level Isp of this kind of
design is irrelevant. If you do not
understand why, then you have no
business at all using my numbers, for any
purpose whatsoever.
The exit diameter computes as 121.7 inches = 3.09 m when I
do this. This engine design sizing experiences
expansion bell flow separation below about 20 kft at its max 4400 psia chamber
pressure, and below around 55 kft at its
min chamber pressure of 880 psia (which assumes 5:1 pressure turndown). It CANNOT be used at sea level under any
circumstances whatsoever!
Figure U-1 shows the CF trend with altitude for an engine
sized this way. Figure U-2 shows the
thrust vs altitude for an engine sized this way. Figure U-3 shows the Isp vs altitude for an
engine sized this way. Bear in mind that
below the flow separation altitudes I indicated, such engines CANNOT be successfully used at
all! That was 20 kft for full thrust
setting, and 55 kft for min thrust
setting.
That 381 sec vacuum Isp compares very well with the 380 sec
Isp listed on Wikipedia for the vacuum version of the Raptor engine. Only the combination of very high chamber
pressure and very large expansion ratio allows this to occur at all! That high chamber pressure is something still
to be demonstrated in engine ground tests, as of this writing! As of this writing, this thing is not yet ready to fly at its
claimed ratings!
At Ae/At = 200 and the same 19.2-inch throat diameter as the
sea level design, the exit diameter is
near 121.7 inches, which is 3.09
meters. At full-thrust setting, this vacuum engine pulls the same 1316
lbm/sec (per engine) from tank storage as the sea level engine. My specific impulses are computed from the
flow rates out of tank storage, not just
the nozzle flow rates. These flow rates are
NOT the same if any pump drive gas is dumped overboard!
This result confirms exactly what I said in the original
article: a sea level LOX-LCH4 engine
generating 330-ish sec Isp at sea level WILL NOT generate 380 sec Isp in
vacuum; its vacuum Isp is closer to only
360 sec. Period! End of issue!
Also accordingly, any such vacuum
design that will generates ~380 sec Isp will NOT be usable anywhere near sea
level! There is NO WAY AROUND THAT! Period!
End of issue!
An engine using those same propellants which generates 380
sec Isp in vacuum is one that ABSOLUTELY CANNOT be used at sea level! Mixing those two numbers (as they are
reported on Wikipedia for the same engine) is a SERIOUS MISTAKE! Please bear that in mind!
Advertising hype is not truth, as we all already know!
Figure U-1 – Estimated CF vs Altitude for a Vacuum Raptor
Engine
Figure U-2 – Estimated Thrust vs Altitude for a Vacuum
Raptor Engine
Figure U-3 – Estimated Isp vs Altitude for a Vacuum Raptor
Engine
Update 9-30-19: Figure U-4 shows the images of the spreadsheet sections used to compute the performance vs altitude plots. Note that the correspondence in geometry is close but not perfect: sea level "Raptor" throat diameter was estimated as 8.604034 inches, while the vacuum "Raptor" throat diameter is reported as 8.604105 inches.
These are only estimates, I got "close". Not "perfect". (That's an inside joke, by the way! These estimates are only "good" to 3 or 4 significant figures!)
Figure U-4 -- Spreadsheet Section Images for Vacuum "Raptor" Estimates
These are only estimates, I got "close". Not "perfect". (That's an inside joke, by the way! These estimates are only "good" to 3 or 4 significant figures!)
Figure U-4 -- Spreadsheet Section Images for Vacuum "Raptor" Estimates











Check this enviromental report about spacex new rockets.
ReplyDeletehttps://www.google.com/url?sa=t&source=web&rct=j&url=https://netspublic.grc.nasa.gov/main/20190801_Final_DRAFT_EA_SpaceX_Starship.pdf&ved=2ahUKEwjcrZ2ZsPDkAhXu0aYKHbvIBiUQFjAAegQIAhAB&usg=AOvVaw0rWH6feFHU3gj4fo-G7QWu
Page 169 onwards. If the link works.
This is very impressive work. Indeed, they do fit with the most recent figures on the Raptor engine!
ReplyDelete