This is a rough estimate of what might be done for landing men (two-way) or cargo (one-way) on Mars, with as common a set of hardware, as is practical. These are ballpark pencil-and-paper calculations. They serve as good start-points for investigators that have access to appropriate trajectory computer programs.
Entry is assumed to be from circular orbit at 200 km altitude, by minimum de-orbit burn conditions. Direct entry from Hohmann transfer orbit conditions (or any other transfer orbit conditions) is NOT covered by these results.
Entry conditions are limited to 3.469 Km/s velocity at 135 Km interface altitude, with a trajectory depression angle of 1.63 degrees. Both the manned and unmanned vehicles are assumed to have hypersonic ballistic coefficients of 1200 kg/sq.m, with no retro thrust during the entry hypersonics.
Under these assumptions, end-of-entry conditions are 8 Km altitude at local Mach 3, nominally 729 m/s, 1.63 degrees depressed below horizontal. Because of the low altitudes at end-of-hypersonics, it is assumed that no chutes or ballutes are used. There is simply not time and room for these to deploy or to be effective. Landing is by retro thrust only.
Methods
End of simple ballistic hypersonic entry at local Mach 3 is assumed as the start-point for these calculations, per the results of reference 1. The ballistic coefficients of the manned and unmanned landers are assumed to be equal at 1200 kg/sq.m, per the results of reference 2, for vehicles in the 60 metric ton class at entry.
Post entry, it is assumed that the pilot (or autopilot) pitches the vehicle to zero angle with respect to local horizontal, and makes a burn to “kill” all the horizontal velocity. This presumes that vertical velocity will increase under gravity. In actuality, a real pilot will angle his burn slightly downward to “kill” the vertical gravitational acceleration as well, but the net effect is very nearly numerically equal.
This has to be done at a high-enough gee level to reduce the gravity-induced vertical velocity and descent distance to acceptable values. Here, those were merely “judgment calls” at time intervals around 1 minute, so that final altitude was “close” to half the initial value. An average constant acceleration approach was used to relate velocity increment to distance covered (and the resulting time). The basic delta-vee was by simple rocket-equation estimation, leading to end-of-interval vehicle masses and propellant-consumed masses.
Once the horizontal velocity is zeroed, there is a residual vertical velocity needing to be zeroed by the time a “practical” altitude is reached. This final altitude was arbitrarily set at 200 meters. The same kind of rocket-equation delta-vee was used, with thrust levels raised by one Martian gee (0.381 Earth gee) to offset the vehicle weight, since orientation is now vertical. Again, average acceleration and average mass levels set the thrust, via the constant average acceleration assumption.
From 200 m, the vehicle is a “tail-sitter” on its own thrust vector at low velocity. The average transit velocity downward must be fast enough to save fuel, but slow enough to be practical. A triangular waveform is the easiest to “analyze”. An average 10 m/s downward was used here, rather arbitrarily, in order to limit total propellant burn. Peak downward is 20 m/s, with 0 m/s at each end of the interval.
For the rocket equation, MMH-NTO propellants were assumed, but with engine cant angle 10 degrees lowering the effective specific impulse. This aids plume and flowfield stability while still supersonic. A short expansion bell, possibly scarfed, was also assumed, for packaging geometry reasons. The net result was lowering a short-bell 305 sec specific impulse to a canted 300.4 sec specific impulse. The effective exhaust velocity for the rocket equation is then pretty close to 2946 m/s.
For the manned lander case, there must be an ascent vehicle capable of returning to LMO, without plane changes (same assumption as for descent). It is also assumed that the same engines serve for ascent as served for descent. The empty descent propellant tanks, cargo, aeroshell, and associated framing structure are left behind. The heat shield is assumed to be “blown away” explosively in segments, at end of hypersonic entry. This vehicle has landing legs and a bottom frame structure. Inert mass fraction is assumed to be near 10%.
For the unmanned, one-way cargo lander, there is no ascent vehicle. That mass allowance goes into deliverable cargo within the aeroshell. All else is the same.
For the manned ascent vehicle, it is assumed that there are three men in a nominal crew. These men ride in a capsule that needs ascent abort capability, so that they might be rescued using a second lander. Thus, the crew cabin capsule should have at least 4 seats, for the rescue pilot, plus the crew of 3 needing rescue. Such a crew cabin capsule might resemble a stripped-down Spacex “Dragon” without the unpressurized trunk (service) module. Herein, a capsule mass in the 4-5 ton range was assumed.
Basic Trajectories
See Figures 1 and 2 below. Per reference 1, peak entry deceleration gee level is about 0.7 standard (Earth) gees. There is no retro thrust during hypersonic entry. At end of entry (about local Mach 3), the 2-ton heat shield is jettisoned as several segments, and the engines (4 to 6 of them) are started. Horizontal velocity is “killed” at about 1.5 standard gees average retro thrust, while at worst, the vertical velocity is allowed to accumulate gravitationally.
The vehicle pitches up vertical, at no horizontal velocity, in the vicinity of 3.4 Km altitude, with at worst about 185 m/s vertical downward velocity. This vertical velocity is “killed” at about 0.9 standard gees deceleration retro thrust, with a terminal altitude near 200 m.
From that altitude, thrust is varied about the weight value at a nominal 0.381 standard gees. Initially, thrust is cut and the vehicle allowed to accelerate downward. This is followed by a thrust throttle-up to kill all vertical velocity, just as the vehicle touches down.
Basic rocket propulsive characteristics are given in Figure 3.
The ascent trajectory is illustrated in Figure 4. This was figured from the rocket equation, factored to allow for gravity and drag losses on a fast-ascent trajectory with a slender vehicle. Gravity losses were factored down by Martian 0.381 gee from “the usual 5%”. Drag losses were factored down by the Martian 0.7% density ratio from “the usual 5%”. Net velocity increment factor was thus 1.0194.
Results – Manned Lander
The manned lander was figured with an ascent vehicle whose crew cabin capsule masses 4 to 5 metric tons. This capsule needs an ascent abort capability, rather like a Spacex “Dragon” with the Super Draco thrusters and some landing legs. It would have to be substantially stripped-down, and without a trunk section (service module). Depending on whether this capsule was 4 or 5 tons, there is room to carry 2 to 6 metric tons of cargo from LMO to the surface. This would include any rover car, exploration equipment, surface “inflatable Quonset hut” habitat, and life support supplies for the landing duration. The crew of 3 is included in the mass of the ascent vehicle (and in that crew capsule). See Figure 5. The aeroshell sectors fold down to double as unloading ramps.
Results – Unmanned Cargo Lander
The one-way unmanned cargo lander uses the same engines, but these are mounted directly on the descent frame, without any ascent vehicle. The ascent vehicle mass adds to cargo capacity, which is then pretty close to 25 metric tons. Most of the descent propellant is packaged where the ascent vehicle would have been. See Figure 6. Like the manned vehicle, the aeroshell sectors fold down to double as unloading ramps.
Update 8-13-12
Revised Figure 5 to show corrected structure weights on ascent and manned descent vehicles. Added Figure 7 to give weight statements and miscellaneous data. Note that the structural weight of the descent vehicle is rather low. The most-likely-needed added structure, whatever it might be, will have to come out of the cargo weights. The 5-ton crew capsule on the ascent vehicle thus looks more attractive.
References
1. G. W. Johnson, “Big Mars Lander Entry Sensitivity Study”, posted 8-12-12 on http://exrocketman.blogspot.com.
2. G. W. Johnson, “Rough Correlation of Entry Ballistic Coefficient vs. Size for “Typical” Mars Landers”, posted 7-25-12 on http://exrocketman.blogspot.com.

Figure 1 – Basic Lander Trajectory Data
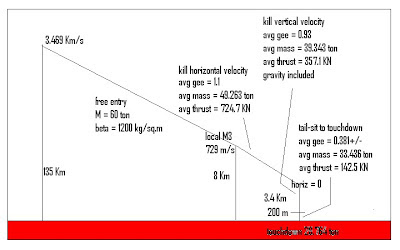
Figure 2 -- More Trajectory and Vehicle Data

Figure 3 – Propulsive Assumptions and Data

Figure 4 – Ascent Requirements

Figure 5 – Manned Lander with Ascent Vehicle, Same Engines

Figure 6 – Unmanned One-Way Cargo Lander, Same Heat Shield, Frame, and Aeroshell

Figure 7 - Weights and Miscellaneous Data
Second Update 8-16-12
I forgot to clarify exactly how I did those post-hypersonic trajectory estimates. I considered the velocity changes required as compared to rocket equation delta-vee, including vertical increments due to gravity. I did not include any corrections for the retarding force of aerodynamic drag, for three reasons: (1) not including drag effects puts more margin into the required rocket equation delta vee, (2) drag is already a smaller force compared to weight or inertia forces on Mars due to the thin atmosphere (see deceleration gees at Mach 3 from the entry data), and (3) there is good reason to believe that a retro-thrust jet into the oncoming supersonic slipstream will cut drag to about half of the no-thrust value.
Just post Mach 3, the basic idea is to zero out the dominant horizontal velocity component. Effectively, I just zeroed-out the entire velocity component, setting velocity at Mach 3 equal to the rocket delta vee required. There was no corrective weight term included in the corresponding thrust. This has to be done in a reasonable time (which sets that thrust level), such that the end-of-interval altitude is still acceptable. That altitude is set by the gravitational free-fall during that interval.
Without a weight-cancelling force, the vehicle accelerates downward at Martian gravity acceleration, even as it decelerates horizontally. End of hypersonics was 8 km nominally, and about 3 to 4 km at zero horizontal velocity seemed “reasonable” to me. The resulting vertical velocity build-up must then be cancelled. It is equal to the new rocket delta-vee, but the net acceleration-induced thrust level corresponding to it must be increased by vehicle weight, to achieve this type of motion in vertical flight. That net vertical deceleration must further terminate at a “reasonable” altitude for beginning the “tail-sitter” descent phase. I picked an arbitrary 200 meters for that altitude.
The final “tail-sitter” portion of the descent must average a reasonable pace, or else too much propellant is burned. My numbers were pretty arbitrary at 10 meters per second average, in a triangular waveform peaking at 20 meters per second, with 0 meters per second at each end. The time to descend (in this case 20 seconds) sets the total impulse, and therefore the propellant burn. Thrust levels will be variable, but very close to vehicle weight on Mars.
The reason to believe that retro thrust reduces drag is from the old Sighard F. Hoerner “Fluid Dynamic Drag” book, which he published himself about 1965. In the Chapter 20 “Practical Results” section, there is a wind tunnel data plot in his figure 27 for a Mercury capsule-like shape in supersonic flow, with a retro thrust jet simulated by high pressure air. For a retro thrust coefficient of 0.16, drag coefficient was slightly less than half the zero-thrust value. That retro thrust coefficient was retro thrust force divided by the product of dynamic pressure and frontal blockage area, similar to drag coefficient.
For the ascent vehicle, I did include gravity and drag effects in a simple factor that knocks down delta vee from the rocket equation value. I typically use 5% gravity loss and 5% drag loss for slender vertical launch rockets here on Earth. Those I ratioed-down by Mars gee (0.381) on gravity, and Mars surface density ratio to Earth standard (0.007) on drag. The knockdown factor so obtained is 1.0194.

No comments:
Post a Comment