Update 3-14-21:
This and similar earlier articles were done to help define what the Spacex "Starship/Superheavy" design might be capable of achieving, once all its evident problems are solved. While prototypes have begun to fly, the design is obviously still quite immature. Landing on a reinforced concrete pad is still a severe problem. Landing on dirt is obviously completely out of the question. Slosh and ullage in the propellant tanks still seems to be a problem, as are leaks and unwanted engine bay fires. Spacex has a long way to go before this design will be ready. Yet its potential looms quite large. So the massive effort that is needed would seem to be worth it.
--------------------------------------------------------
I recently updated my reverse-engineering estimates for what
a Spacex “Starship/Superheavy” vehicle can accomplish flying to circular low
Earth orbit (LEO) from eastward launch.
These are based on the best available information about the vehicle from
the Spacex website, the Spacex user’s
manual for flying on this vehicle, what
some observers have published for inboard profile details, and what Wikipedia shows for details like
inert masses.
There is still a big difference between the Starship test
flight prototypes Spacex is flying, and
its proposed orbital transport design.
This shows up in the inboard profile,
and in the landing legs. The
prototypes are presumed to be heavier in construction, since data is still being obtained. The hull forward of the propellant tanks is
mostly empty, whereas in the proposed
transport vehicles, those spaces are
rigged for all-cargo, passengers plus
some cargo, or extra tanks for a tanker
version.
Figure 1 compares the prototypes and the proposed
versions, giving the relevant data as
appropriate. All figures are at the end of
this article. Prototypes are flying on 3
sea level Raptor engines, while the
proposed flight vehicle has 3 sea level and 3 vacuum Raptor engines, for a total of 6 engines.
Figure 2 gives similar pertinent data for the Spacex
Superheavy booster design. It depends
upon the source as to how many sea level Raptor engines power this stage. Currently Spacex says 28, but in the recent past I have seen numbers as
high as 33, or even more (37 in one
older presentation). This is a critical
issue for acceptable kinematics right off the launch pad. Mr. Musk himself has said (in his Boca Chica
presentation in front of a prototype) that he wants to see liftoff
thrust/weight ratio close to 1.5.
I have already reverse-engineered the performances of the
sea level and vacuum Raptor engines.
This includes the full intended rated chamber pressure, as well as throttled-back performance, which is lower. These numbers are included here as Figures 3
and 4. The effects of altitude are
included specifically, at both max and
min chamber pressure. These engines
share exactly the same powerhead. They
differ only in the expansion area ratio of their exit bells. In the predicted performance tables listed in
the figures, shaded cells indicate flow
separation due to excessive backpressure.
The basic mission data are given in Figure 5. The Superheavy booster gets flown back from
the stage point, while the Starship
upper stage continues on to orbit. The
numbers are for an eastward launch. The
circularization burn for final orbit entry of the Starship upper stage is
presumed included in the factored velocity requirement to orbit.
The booster, much
lighter without the upper stage, thrusts
to kill the downrange velocity, and for a
little bit more speed, both up-range and
upward. The idea is a net 45 degree
upward trajectory, coasting back toward
the launch site on a more-or-less parabolic trajectory. This will convert by drag to a downward fall
toward “entry”, which is really just
hitting denser air and seeing larger wind pressures. There is an entry burn to reduce speed down to
near Mach 1 at fairly low altitude, with
subsequent fall to the landing burn from a presumed Mach 1 terminal velocity in
the dense air.
There is a deorbit burn,
followed by hypersonic aerobraking,
with the Starship upper stage.
Once the entry hypersonics are over,
the vehicle assumes the “belly-flop” attitude to limit downward
velocity. At low altitudes, broadside drag limits the fall velocity to
quite modest values, as already seen in
prototype flight tests. Near the
surface, the vehicle “flips” to vertical
attitude by means of engine thrust (and aerosurface action), and then lands retro-propulsively, as the prototypes currently do.
Figure 6 indicates how the gravity and drag losses were
estimated, and how they were apportioned
among the various burns during the mission.
The booster ascent is initially vertical, and bends near horizontal upon reaching the
staging altitude, which is essentially
exoatmospheric. I used the simplest
means of estimating the gravity and drag loss totals, and apportioned all the drag loss and most of
the gravity loss to the booster stage burn.
This is in accord with the best recommendations
of Ref. 1.
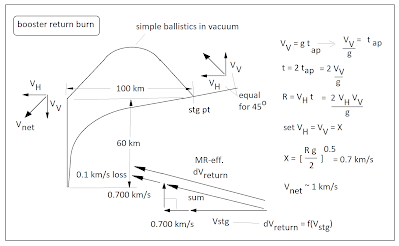
Figure 7 indicates exactly how the parabolic ballistic
trajectory of the booster flyback was estimated. The requisite horizontal and vertical
velocity components, which are equal at
45 degrees, were determined from the
required range (merely an educated guess here).
The net burn delta-vee sums this horizontal and the magnitude of the
staging velocity, for the horizontal
component. The vertical component is
alone. The “ideal” or kinematic
delta-vee is the vector sum of those components. To that,
the gravity loss estimate is added (there being no drag loss at
altitudes that high).
Figure 8 indicates the details of the booster flyback entry
and landing burns, including the
assumptions made. A potential energy
difference to the presumed entry altitude is added to the kinetic energy coming
out of the parabolic arc. That is the
kinetic energy at entry altitude in the absence of any drag loss. Converted back to velocity, the difference between that and the desired
entry speed is the “ideal” or kinematic delta-vee for the entry burn. This gets the estimated gravity loss added to
it for the mass ratio-effective delta-vee.
The terminal speed at the surface,
factored up, is the landing burn
delta-vee.
Figure 9 summarizes which engines get used for each of the
burns, and what the estimated
performance of the selected engines are, at those conditions. Note that the booster uses sea level
Raptors, sometimes at sea level, sometimes in vacuum, and an average of those two during its ascent
toward the stage point. For the entry
burn, I used the 50 kft (15 km) altitude
performance values.
The upper stage spacecraft uses its vacuum Raptors during its
ascent from stage point to orbit. It
uses a vacuum Raptor for the deorbit burn.
The landing burn is made with sea level Raptors operating at sea level. Full thrust settings were presumed.
The figure indicates where vehicle thrust/weight ratio ought
to be 1.5 (or more) to get acceptable kinematics in vertical flight against
gravity. It also indicates where the
Spacex user’s manual (Ref. 2) says that vehicle accelerations should not exceed
6 gees.
One worksheet in the spreadsheet does the entire
analysis. Its image is given in Figure
10. User inputs are highlighted
yellow, with significant results
highlighted blue. Pertinent comparison
data are highlighted green. This
spreadsheet requires user iteration to achieve “closure”. There are two variables that must be
optimized: the stage point
velocity, and the payload carried by the
Starship upper stage. Spacex
advertises “100+ tons to LEO”. This
analysis indicates 171 tons might be feasible.
Instructions are on the worksheet; these require first determining the stage
point velocity such that the required ascent delta-vee equals what the stage
can deliver. That presumes zero
propellant remaining after the booster flyback,
entry and landing. You do this
with some “reasonable” payload in the Starship upper stage.
Once that is done,
you maximize the payload carried in the Starship, such that its ascent delta-vee capability
just matches the requirement. This is
done such that deorbit, entry, and landing results in zero propellant
remaining, when landing with the full
payload. That last covers the abort
requirement if payload cannot be delivered and unloaded on orbit. This is a highly-constrained analysis, not general.
You may or may not have to readjust stage point
velocity, then payload, to fully converge the analysis.
There are inputs for the number of Raptor engines operating
in each stage for each of the pertinent burns.
The resulting estimated thrust/weight ratios are computed from these
engine number selections and the appropriate thrust performances. The best guesses for thrust/weight criteria
are listed alongside those results.
Results and Conclusions
This analysis indicates that Starship/Superheavy might be
capable of delivering as much as 171 metric tons of payload to a low Earth
orbit from an eastward launch. Spacex
claims “100+ tons”, and these results
indicate significantly more than that might well be feasible. The previous analysis (Ref. 3) got a somewhat-lower
payload number (still greater than 100 tons) for the same circumstances.
This calculation determines the propellant requirement for
Starship to deorbit and land, and limits
payload capability of the Starship to make sure there is propellant on board
sufficient to make the landing. It does
this under the assumption that the full payload is carried back down to the landing, in order to cover an abort possibility where
payload cannot be offloaded before a descent is required.
Similarly, the
propellant required for the Superheavy booster stage to execute the
flyback, entry, and landing is determined. Then the staging velocity capability of the
Superheavy is determined such that there is enough remaining propellant to
land. That determines the stage point
velocity for the mission. This is done
with the ignition mass of the loaded Starship as the “payload” of the Superheavy.
These results are based on certain guesses for stage inert
masses. If there is growth in inert mass
beyond that assumed, it must come
straight out of payload capability. It
is also based on maximum propellant loads for each of the stages. Carrying less propellant reduces payload
capability. Or, looked at another way, reducing payload carried reduces the required
propellant load. That analysis is not
done in this spreadsheet! This is not
a generalized performance-prediction analysis!
Possible Future Analyses
Sending Starship to an elliptical Earth orbit instead of low
circular, has been touted as the way to
use Starship/Superheavy for trips to the moon and back, without any refueling on the moon. The velocity requirement to reach such an
orbit is higher, reducing the lunar
payload capability below the estimate here.
That mission is challenging enough that return payload likely needs to
be reduced, or even zeroed. This spreadsheet could be used to determine
what payload might be delivered to that elliptic orbit. The lunar mission itself needs to be analyzed
separately, not with this tool. Same for
Mars.
References
#1. Fundamentals of
Elliptic Orbits, dated 5 March
2021, by G. W. Johnson, located at
http://exrocketman.blogspot.com
#2. Starship User’s
Guide, revision 1.0, dated March 2020, downloaded from Spacex.com as pdf
#3. 2020 Reverse-Engineering
Estimates for Starship/Superheavy, dated
25 May 2020, by G. W. Johnson, located at http://exrocketman.blogspot.com
Figure 1 – Best Available Data for “Starship”
Figure 2 -- Best
Available Data for “Superheavy”
Figure 3 – Best Reverse-Engineered Model of the Sea Level
Raptor
Figure 4 – Best Reverse-Engineered Model of the Vacuum
Raptor
Figure 5 – Circular Low Earth Orbit Mission Characteristics
(160-600 km Altitudes)
Figure 6 -- How the
Gravity and Drag Losses Were Estimated
Figure 7 – Details for the Booster Flyback
Figure 8 – Details for the Booster Entry and Landing
Figure 9 – Engine Performance Assumptions For the Mission
Figure 10 – Spreadsheet Results for Mission Performance
Estimates
Update 9 March 2021:
I copied and edited the worksheet to represent a 300 x 1400
km elliptic orbit. Those changes are
shown in Fig. 11. The results are given
in Fig. 12. Payload reduces to 144
metric tons, staging is unchanged.
Figure 11 – Orbit and Input Data Changes for 300 x 1400 km
Elliptical Orbit
Figure 12 – Spreadsheet Results for 300 x 1400 km Elliptical
Orbit
Looking at even higher elliptical orbits, and assuming radiation dangers to cargo and
crews can be addressed, I found that
about a 300x4000 km orbit reduces payload to about 103 metric tons, with the same staging point. Orbit data are in Fig. 13, results are in Fig. 14.
Figure 13 – Data Regarding the High Elliptical Orbit
Figure 14 – Results for the High Elliptical Orbit
Note that Spacex promises payload delivery of “100+
tons”. What I found for the high
elliptical orbit is pretty close to that figure. The lower elliptic orbit has a higher max
payload figure, and the low circular
orbit a higher max payload still. This
is summarized in Fig. 15. Note also that
radiation protection becomes a serious issue for apogees above 1400 km, which puts the spacecraft in the Van Allen
belts.
Figure 15 – Overall Results Summary for the 3 Earth Orbits
Update 3-13-2021:
While pursuing use of Starship to perform unrefueled lunar
landing missions, I needed to analyze
some higher-still elliptical orbits for Starship/Superheavy to reach. These were a 5000 km apogee altitude, a 10,000 km apogee altitude, a 20,000 km apogee altitude, and a 30,000 km apogee altitude. Those results from the spreadsheet are given
in Figures 16, 17, 18,
and 19, respectively. The trend is quite clear: less and less payload can be delivered to
orbit, as the orbit apogee altitude
increases.
Bear in mind that the “base” of the Van Allen radiation
belts is about 1400 km altitude (lower for the South Atlantic Anomaly). All these orbits penetrate quite far into the
radiation belts. Radiation hardening of
cargo, and radiation shelter protection
for any crew, are simply required.
Bear also in mind that all of these orbits (this update and earlier) were computed under the assumption that an abort back to the surface be feasible, with full payload still aboard. That does raise the landing propellant budget, and it raises the landing thrust requirement.
Figure 16 – Results for 300 x 5000 km Elliptical Orbit
Figure 17 – Results for 300 x 10,000 km Elliptical Orbit
Figure 18 – Results for 300 x 20,000 km Elliptical Orbit
Figure 19 – Results for 300 x 30,000 km Elliptical Orbit
The overall trend summarizes as the following table:
Orbit (km altitudes) max payload (metric tons)
300 x 300 171
300 x 1400 144
300 x 4000 103
300 x 5000 92
300 x 10,000 59
300 x 20,000 30
300 x 30,000 17
For those interested,
this spreadsheet I used to estimate Starship/Superheavy performance to
these orbits is named “SS SH 2021”, for
my 2021 reverse-engineering estimates of Starship/Superheavy. These calculations include booster flyback
and recovery, plus Starship deorbit and
landing (recovery). Each destination
orbit has its own worksheet. These are
named (so far) as follows:
Orbit worksheet
name
300 x 300 circ LEO
300 x 1400 ellip LEO
300 x 4000 high ellip
300 x 5000 5k apo
300 x 10,000 10k apo
300 x 20,000 20k apo
300 x 30,000 30k
apo



















No comments:
Post a Comment