Purpose: to find out how different a manned Mars lander design might be, under different assumptions about the extrapolation of ballistic coefficient β to a “reasonable” lander mass. I previously assumed (reference 1) a net average trend from all prior experience. This study assumes two different trends for the US probes landing on Mars, and the historic US manned capsules that landed upon Earth.
Scope was limited to a 60 metric ton entry mass for the Mars lander, chemical propulsion with storable monomethyl hydrazine (MMH) and nitrogen tetroxide (NTO) propellants, and an ascent vehicle in the neighborhood of 3.66 meters diameter. That last dimension matches the Spacex “Dragon” capsule, which in a much-modified form, might well be the descent/ascent abort sub-vehicle for astronauts trying to land on, or return from, the surface of Mars.
Re-Analysis and Curve-Fit of β Data
The original data set was researched and combined from US Mars lander probe data in reference 2, and the results of an internet search for data concerning US historic manned capsules (see reference 3). In reference 1, those data were combined into a single average entry trend at the average exponent, used with the Apollo data as a reference scaling point. That trend is a power function on lander mass:
β = βref (mass/ref.mass)^exponent where “ref” is the mass and β at some reference design
The results from reference 1 said that a manned lander in the 60 metric ton class at entry would have a β near 1100 kg/sq.m, if the hypersonic drag coefficient was near 1.3. There are very probably two things wrong with that estimate.
(1) The average Apollo hypersonic drag coefficient was actually nearer 1.5 than 1.3 (see reference 3).
(2) The manned capsules were designed for a much-different entry environment than the probes at Mars, and with much less entry protection knowledge available back then (ca. 1960).
Accordingly, in this article, I treat the two subsets of data as separate trends, and extrapolate them separately. Amazingly enough, the two separate trends predict about the same β at 60 tons mass: near 400 kg/sq.m. This results in a much-different estimate of available volumes and diameters, for crudely the same weight statement. (Actually, the final touchdown analysis is different, because end-of-entry conditions, especially altitude, are different, leading to a revised weight statement).
The basic data for both the US Mars lander probes and the historic US manned capsules are tabulated in Figure 1 below. The calculations of entry ballistic coefficient data are tabulated in Figure 2.
Since a power-function curve fit is being employed to model β versus entry mass, the appropriate curve-fitting technique is a straight-line (slope) model on a log-log plot, as in Figure 3. The natural logarithm could have been used, but was not, for convenience with data in scientific notation. As Figure 3 indicates, these “fits” are pretty good, if two separate trends are assumed. The result of this power-function modeling in absolute units is given in Figure 4. The two fits are “pretty good” visually, referenced as they are to Apollo and the MSL (“Curiosity”).
Extrapolation to 60 Metric Ton Entry Masses
Figure 5 presents the two separate power-function curve-fits on a log-log plot, extended to very large lander masses on the right. The results appear to be identical “not very far away” at 60 metric ton entry mass. However, one should be suspicious, because every unit of abscissa extrapolation on this plot is another factor of 10 on entry mass, outside the range of known data. Further, log-log plots are not very discriminating, regardless of the logarithm base used.
This is more evident in the corresponding absolute-units plot, Figure 6. It is very clear that we really are in “new territory”, by about a factor of 10 relative to Apollo, and more still, relative to MSL. However, it is gratifying to see that the two disparate trends agree on β at that particular 60-ton entry mass. 400 kg/sq.m thus seems to be a more “reasonable” estimate of 60-ton lander β, than the earlier 1100 kg/sq.m value that was used in reference 1.
Results for Lander Design Proportions and Sizes
Assuming we want a shape with about the same “bluntness” as Apollo, and that we want a “tumble-home” conical angle intermediate between that of Mercury/Gemini and Apollo, then we want a heat shield radius/diameter ratio near 1.1-1.2, and we want a conical half-angle near 30 degrees. Those proportions are given in Figure 7. Specifying mass (60 tons), β (400 kg/sq.m), and the average hypersonic drag coefficient (1.5), sets the frontal blockage area and the diameter.
For this analysis, I used a heat shield diameter of 11.28 m, and a heat shield radius of curvature of 12.4 m. Note also that we want the Apollo-type corner radius, as this typically acts to reduce local heating at the corner. No detailed corner radius was specified in this analysis, just the existence of one.
The ascent vehicle diameter shown in figure 7 is arbitrary, except that we would like this to match an existing capsule that might provide some kind of abort capability, during both descent and ascent. The value shown matches the Spacex “Dragon”, which in a much-modified form, might fulfill this role.
The conceptual internal layout of such a lander concept is given in Figure 8. The main weight-saving idea here is to use the ascent vehicle engines as the descent engines, just “sucking” from a separate descent propellant supply during that phase of flight. A wide range of engine throttleability will be required, but this has already been demonstrated to be technologically feasible. A part of the conical volume around the ascent vehicle will contain descent propellant, the rest may contain cargo, supplies, and equipment, that are to be delivered to the surface.
Such a lander comprises a heat-shielded conical descent shape with a “pointy” core (the ascent vehicle) sticking out on-axis (so that the pilots can see around themselves). Within a limited range of angles-of-attack (perhaps +/- 15 degrees), lifting entry trajectories may be flown, although, that capability is not assumed herein, for crude-overall design analysis purposes.
Unmanned cargo landers do not necessarily share this “pointy core” sticking out past the basic 30-degree cone shape, and thus may be capable of more lifting-maneuver capability during entry (near a full 30 degrees angle of attack). That can only contribute positively toward precision landings near a homing beacon.
The ports through which the engines fire must be opened, before the engine thrust deceleration can be used to provide a reliable separation of the heat shield in the face of the oncoming supersonic wind blast. This is also shown in Figure 8. Auxiliary solid propellant cartridge motors may be needed to safely effect this separation, also a well-proven technology. The MSL heat shield was about 1.6 inches (4.1 cm) thick. Using that thickness at a specific gravity of about 1.5, there are about 6.1 tons of silica-phenolic-like ablative in that heat shield. With support structures and separation equipment, a guess of 6.5 to 7 tons for the 11.28 m diameter heat shield assembly is not unrealistic. This is much larger than the 2 ton heat shield in reference 1, primarily due to the much larger diameter.
“Back-of-the-Envelope” Entry Re-Analysis
The 2-D Cartesian approximation of entry dynamics and convective heating is given in Figures 9 through 13 below. These are not a lot different from prior results except that the end-of-entry altitude (based on Mach 3 speed) is quite a bit higher at the lower β. In this case, end-of-entry is nearer 17.2 km altitude. This is still well below the 25-30 km probe experience, but much higher than the terminal altitude reported in reference 1. This required a new analysis of rocket braking to touchdown.
The basics of this entry analysis were reported in reference 2, and updated by me in reference 4 to spreadsheet integrations of total convective heat load. This analysis is adequate for orbital and direct entry estimates at Mars, but not for aero-braking calculations. This is a 2-D Cartesian approximation of entry (only) at a fixed path angle to the local horizontal. It was adequate for warhead re-entry dynamics ca. 1956. Entry calculates as 1425 s (23 minutes and 45 seconds) from entry interface to the Mach 3 point.
Rocket Braking to Touchdown
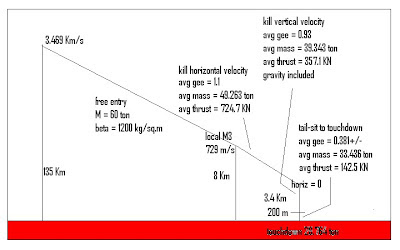
The analysis here is similar to that of reference 1. Entry requiring heat protection is assumed “done” at Mach 3, as before. This velocity is at the same 1.63 degrees entry from low Mars orbit as in reference 1, leading to a vertical velocity component of 19 m/s, and a horizontal velocity component of 675 m/s. Touchdown analysis is done with zero drag forces assumed, due to the presence of retro thrust plumes that reduce drag further than expected, by at least a factor of 2, as discussed in reference 3, and also the extreme low density of the Martian atmosphere. There is no attempt made to use an aerodynamic decelerator, as was discussed in reference 1, due to very stringent time constraints.
Vertically, velocity is accumulated downward due to Mars gravity as the vehicle makes a burn (parallel to the local horizon) to kill all the horizontal velocity component. This is arbitrarily done so that the altitude at which the horizontal velocity zeroes is half the terminal entry altitude (which sets the average deceleration level). Thrust levels are set by that deceleration level, only in this phase.
Then the vehicle pitches up vertical (engines still burning) and kills all the accumulated vertical velocity but an arbitrary-but-“reasonable” 20 m/s, by the time it reaches the “reasonable” altitude of 200 m. Thrust levels are set by the net (or effective) deceleration plus average weight in this phase.
From there, it descends at an average 10 m/s to the surface (20 m/s to zero in 200 m). In this phase, thrust is very nearly equal to weight. The propellant mass expelled in this phase is quintupled in the design, to provide a terminal maneuver capability of around 100 seconds in order to avoid obstacles.
In each of these three phases, the velocity change is used in the rocket equation to estimate mass ratios and masses at the end of each phase. Mass changes correspond to propellant masses used. The average mass at the average net acceleration gives the base thrust, to which vehicle weight must be added in the two vertical phases.
Velocity, altitude, and mass information for this rocket-braking descent are given in Figure 14. The mere 144 sec interval from Mach 3 to touchdown makes it quite clear why aerodynamic decelerators are not feasible for this kind of a landing. Most parachutes cannot be deployed above about Mach 2.5 speeds, and simply could not decelerate the vehicle subsonic before impact. So there is no point.
Ascent Requirements (Basically Unchanged from Reference 1)
For this analysis, the crew capsule was assumed to be 5.5 metric tons, about halfway between the mass limits used in reference 1. The modified Dragon would be the capsule with a thinner, lighter heat shield, extra propellant on board, and no trunk module. It would carry at most 3 men, plus enough propellant to land on the Super Draco thruster system, without landing legs. No parachute is assumed for the abort scenario, nor were any of those abort scenarios analyzed in detail here.
That crew capsule was assumed to ride as “payload” atop a single-stage MMH-NTO rocket of the same 3.66 m diameter, of 5% inert mass ratio, as has been demonstrated recently for throw-away vehicles. These design requirements are summarized in Figure 15. This is an ascent vehicle capable of reaching LMO, but with zero plane-change capability. It represents the minimum that could (or should) be done. Adding plane change delta-vee increases the size and mass of this ascent vehicle. Big enough, and the entry mass of the lander must be increased, as you quickly go negative for your cargo allowance.
Per the data and methods of reference 5, the absolute minimum theoretical velocity requirement to reach 200 km LMO without plane change is 3.455 km/s. The “traditional” gravity loss on Earth has been about 5% of theoretical velocity. The “traditional” drag loss for a slender vertical launch rocket has been about 5% of theoretical velocity here on Earth. Scaling the gravity loss down by 0.38 gee, and the drag by 0.7% surface density, at Mars, results in a combined gravity-drag loss factor of 1.94% for Mars. Add another 2.7% for design margin, for 3.62 km/s delivered delta-vee, as long as the plane change is zero.
The stubby shapes for the lander considered here probably have twice the normal ascent drag coefficient, but twice near-nothing is still close to nothing. That issue is more properly explored with a real computer trajectory code.
Ascent Vehicle Dimensions and Masses
The ascent vehicle as re-sized is depicted in Figure 16. This vehicle is far shorter than was expected, so that a serial arrangement of fuel and oxidizer tanks is nearly all elliptical head spaces and very little cylindrical space. The appropriate propellant volume-to-cylindrical envelope volume factor is thus probably lower than the 90% that I used. Propellant density data were obtained from reference 6.
However, a lower limit for simple packed spheres is 63%, so we cannot be all that far off. I rounded up my tank length results to compensate a bit for this effect. The capsule and the wild guess for engine length dominate ascent vehicle length, anyway. This is because of the 3.66 m diameter.
Accordingly, a parallel arrangement of fuel and oxidizer tanks is more likely the “best” design choice. There would be only two elliptical heads, with radial bulkheads separating fuel and oxidizer. These tanks would have to be equally pressurized, so that the straight radial bulkheads are structurally practical. Either way, the overall vehicle length is probably not all that far from the value depicted.
For the ascent design, the mass ratio MR is computed from the delta-vee required and the estimated exhaust velocity. The propellant mass fraction (in this case just under 71%) is
PMF = 1 - 1/MR
The payload is a fixed mass at about 5.5 tons, as “guessed” for a Dragon capsule modified for extra propellant and a lightened heat shield, but without its trunk section. The inert (structural) mass fraction (IMF) is assumed to be 5%, as has been demonstrated operationally in throwaway rocket vehicles. This would include the engines as well as the tankage structure.
The payload mass fraction available is 1 minus the propellant and inert fractions, in this case a bit over 24%. The payload mass divided by the available payload mass fraction sets the ignition mass for the ascent vehicle, in this case, not quite 23 metric tons. For storable propellants, it is clear that this ascent can easily be done in a single stage vehicle, as long as orbital plane changes are not required.
As far as the lander is concerned, the entire ascent vehicle is “dead-head payload”, with the exception of the engines themselves. Those engines will “suck” descent propellant from tanks inside the lander, but outside the ascent vehicle.
The study in reference 1 did not compute volumes and lengths for the ascent vehicle, only a weight statement. The shortness of the ascent vehicle obtained here impacts the actual final shape of the descent vehicle, as described in the next section.
Manned Lander Weights and Volumes
I had been expecting a long ascent vehicle to “stick out of” a 30-degree tumble-home conical descent shell. Instead, the ascent vehicle turned out to be quite short. For practical pilotage reasons, as well as safe abort reasons, it is necessary that the crew cabin capsule be located outside the descent shell. Accordingly, I went to a double cone shape not unlike that of the unmanned US Mars probe lander aeroshells.
The construction concept here is a base frame to which an aeroshell frame is attached. The aeroshell panels are attached to those frame elements, and fold down to provide a second function as unload ramps. The base frame supports a segmented heat shield below, and mounts the ascent vehicle above. Inside this shell are 3 or 4 landing legs, extended laterally, then axially, to provide engine clearance.
The volume enclosed by this aeroshell contains both descent cargo and the descent propellant tanks. Again, there is a lot more volume available inside this shell than any conceivable configuration of descent propellant tanks could ever require. Thus, there is plenty of room for lots of very low-density cargo. See Figure 17 for the final dimensions and weight statement.
Note that this analysis indicates that the 3 astronauts could reach the surface of Mars with over 5 metric tons of supplies and equipment. That is quite a remarkable result, especially since it is seemingly easily reached by eliminating the aerodynamic decelerator in favor of simple rocket braking. Note that no retro thrust is required during hypersonic entry in this design, only during the supersonic-to-subsonic deceleration, post-entry.
Unmanned Variant Weights and Volumes
The same basic aeroshell and heat shield could enclose the same set of engines mounted directly to the same base frame, and drawing from the same kind descent propellant tanks, just placed differently. In this case, the rest of the ascent vehicle is deleted in favor of more cargo mass, for which there is plenty of available volume. This unmanned cargo lander design is depicted in Figure 18. Note that the cargo deliverable to the surface is over 28 metric tons, from the very same 60 ton entry mass.
Conclusions
Large lander vehicles capable of taking 3 astronauts to the surface of Mars might have ballistic coefficients nearer 300-500 kg/sq.m than the 1000-1200 kg/sq.m indicated in reference 1. This change in assumptions affects the detailed numbers, but not the primary outcome: landing large payloads on Mars is not nearly as hard, as has been recently hyped.
The time between end of entry at Mach 3 and surface touchdown is far too short for aerodynamic decelerators to deploy, much less be effective, at ballistic coefficients over about 200-300 kg/sq.m. This is because the end-of-entry altitude is so much lower at the higher ballistic coefficients. Therefore, the preferred approach at high β is to go directly from heat-shielded entry to direct rocket braking for touchdown.
This change in design paradigm turns out to be very feasible for landing crews of 3 with around 4-5 tons of equipment and supplies, in a lander massing no more than about 60 metric tons at entry, while using easily-storable chemical propellants.
The ascent vehicle in this design is of minimal size for no plane change capability. Adding plane change capability adds considerable mass to the ascent vehicle, and also to the descent vehicle that carries it to the surface, in a compounded manner. If plane changes are required, this may be better done by the carrier vehicle in LMO that is launching these landers.
References
1. G. W. Johnson, “Chemical Mars Lander Designs ‘Rough Out’”, posted 8-12-12 to http://exrocketman.blogspot.com
2. C. G. Justus and R. D. Braun, “Atmospheric Environments for Entry, Descent, and Landing (EDL)”, MSFC-198, June, 2007. (Model atmospheres and a description of the 1956-vintage entry analysis)
3. G. W. Johnson, “Blunt Capsule Drag Data”, posted 8-19-12 to http://exrocketman.blogspot.com
4. G. W. Johnson, “Back of the Envelope Entry Model”, posted 7-14-12 to http://exrocketman.blogspot.com (1956-vintage entry analysis updated and adapted to spreadsheet)
5. G. W. Johnson, “Big Mars Lander Entry Sensitivity Study”, posted 8-10-12 to http://exrocketman.blogspot.com (done for entry from LMO at 200 km)
6. Pratt and Whitney “Aeronautical Vest-Pocket Handbook” 12th edition, 21st printing, December, 1969.

Figure 1 – Basic Physical Data

Figure 2 – Computed Ballistic Data

Figure 3 – Curve-Fitting Prior Data on a Log-Log Plot

Figure 4 – Quality of the Two Separate Curve Fits Appears “High”

Figure 5 -- Extrapolation of Both Curve Fits on a Log-Log Plot

Figure 6 -- What Those Extrapolations Really Look Like In Absolute Units

Figure 7 – Lander Design Proportions

Figure 8 – Internal Layout Concept for Lander

Figure 9 – Selected Spreadsheet Images for Entry Analysis

Figure 10 – Entry Results: Velocity vs Slant Range

Figure 11 – Entry Results: Range and Slant Range vs Altitude

Figure 12 – Entry Results: Deceleration Gees vs Slant Range

Figure 13 – Entry Results: Convective Heating vs Slant Range

Figure 14 – Terminal Dynamics Results (Entry to Touchdown)

Figure 15 – Assumptions Made Regarding the Ascent Vehicle

Figure 16 – Final Weights, Dimensions, and Volumes for Ascent Vehicle

Figure 17 – Final Weights and Volumes for Manned Lander

Figure 18 – Final Weights and Volumes for Unmanned Cargo Lander